Next Contents Previous

Comments on the different theories

Let us first discuss some problems inherent to theories based on phase transitions. Phase transition generated magnetic fields have small scales. For instance, the most recent one, the QCD transition, at $ \sim$200 MeV, predicts correlation lengths of 10-11cm, which grow to 10 cm at present. The horizon at the QCD phase transition was 10-6cm, equivalent to 0.2 pc at present. Other phase transitions also predict small scales. The electroweak phase transition took place when the horizon was at only a few centimeters, corresponding to about 1 AU at present. For early phase transitions the expected scale is even worse.

These fields undoubtedly created in phase transitions probably have no connection with present magnetic fields, because there are two mechanisms that can destroy this kind of small scale fields.

First, the subsequent radiation-dominated universe was highly resistive, because of the frequent encounters between electrons and photons. This has been shown by Lesch and Birk (1998). The low conductivity implies magnetic diffusion. These authors gave a diffusion time equivalent to

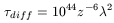
Equation 146   (146)

where $ \tau_{diff}^{}$ is measured in seconds and $ \lambda$, the coherence size, in cm. This time very much depends on redshift, with the initial times being the most destructive, probably just after Annihilation, because of the increase in the photon number density. If we set $ \tau_{diff}^{}$ = $ \tau_{rec}^{}$ (Recombination epoch) and z = zann (Annihilation redshift) we will obtain the minimum scale able to survive from Annihilation to Recombination

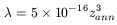
Equation 147   (147)

This $ \lambda$ will grow to its present comoving size

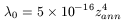
Equation 148   (148)

For zann $ \sim$ 2 × 109, we conclude that the minimum scale able to survive was about 3 kpc, much higher than the scale predicted by the magnetogenesis mechanisms based on cosmological phase transitions.

It is understandable that magnetic fields, and density and radiation inhomogeneities are associated during the radiation dominated Universe. Therefore if matter or radiation overdensity regions, at a certain scale, are destroyed or damped, the same end should be expected for magnetic fields of this scale. It is known (Silk, 1968; Weinberg, 1972) that masses smaller than the Silk mass are damped in the Acoustic epoch, before Recombination. Jedamzik, Katalinic and Olinto (1996) also concluded that MHD modes are completely damped by photon diffusion up to the Silk mass and convert magnetic energy into heat. Damping would also be very important during the neutrino decoupling era. Therefore, small scale fields could have been eliminated before the radiation era.

Therefore, small scale fields, even if they were created in phase transitions, cannot survive the radiation dominated era. They have two enemies: magnetic diffusion and, probably, photon diffusion.

However, we must mention the important work by Brandenburg, Enqvist and Olesen (1993) in which they propose that inverse cascade effects in relativistic turbulence in the expanding medium produce large scales. Then, inverse cascade would save the small scale phase transition magnetic fields. But the existence of a turbulence during this epoch is controversial (Rees, 1987), or at least it would have had a very peculiar behaviour. In fact $ \delta$$ \rho$/$ \rho$ cannot evolve in a random way. If $ \delta$$ \rho$/$ \rho$ is small but positive, it will always increase and remain positive if the cloud mass is higher than the Jeans mass, because of gravitational collapse. The Jeans mass is very low, particularly just after Annihilation, of the order of 1 M$\scriptstyle \odot$, and therefore gravitational collapses, rather than true turbulence, dominated the evolution of initial inhomogeneities. Perturbations of the metric tensor are essential in this era. Even if the inhomogeneities do not grow very fast (as a2) they cannot be neglected. On the other hand, turbulent motions, if they really existed, could not affect scales larger than the horizon, and therefore scales larger than 1 Mpc cannot be produced. In fact, Brandenburg, Enqvist and Olesen predict much lower amplification factors, given the initial very small scales to be enlarged.

These arguments seem to exclude phase transitions as mechanisms providing magnetic fields connected to present fields. Moreover, the model proposed by Harrison (1973) even if historically interesting, and emphasizing the effect of the horizon on the turbulence regime, did not include General Relativity effects, which are not ignorable at all.

Therefore, despite the possibilities of an extended analysis of inverse cascade effects, we favour the hypothesis that large scale fields (larger than the horizon in the radiation dominated era) were produced at Inflation, as deduced in the scenario of string cosmology (e.g. Gasperini and Veneziano 1993a, b). Small scale fields, such as those in galaxies, have two possible origins: a) The large scale inflation magnetic fields were amplified after Recombination as a result of contractions in the process of forming superclusters, clusters and galaxies after Recombination; b) They were generated without seeding by battery mechanisms in the process of galaxy formation.

Irrespective of the exact time and mechanism of magnetogenesis, the effect of preexisting magnetic fields on the birth and structural properties of galaxies has been considered in the literature. Piddington (1969) tried to explain the present morphology of different types of galaxies from the angle between the angular momentum and the magnetic field strength. Wasserman (1978) considered that the formation of galaxies was decided by preexisting magnetic fields and that these were even able to provide the galactic angular momentum. Kim, Olinto and Rosner (1996) extended this work to the non-linear regime.

It is difficult to decide between the two possibilities for the origin of small scale magnetic fields, and therefore to decide what is the origin of galactic magnetic fields. We prefer to argue in favour of the inflationary origin, for the following two reasons, one theoretical and the other observational:

a) We will see that magnetic fields of the order of B0 $ \sim$ 10-9 - 10-8G may be present in the $ \sim$ 100 Mpc long filaments characterizing the large scale structure of the Universe. These structures probably consisted of filamentary concentrations of photons, baryons and possibly other kinds of dark matter, but the energy density was smooth and continuous within a filament. After Recombination, baryons and dark-matter particles begun to form clumpy structures of a different order (superclusters, clusters, galaxies), and the contractions involved produced an amplification, until the present value of about 10-6G was reached. The simulations carried out by Dolag, Bartelmann and Lesch (1999) indicate that initial magnetic field strengths of 10-9 G at z = 15 provide an amplification of three orders of magnitude in cluster cores. Therefore if B0 was 10-9 - 10-8G in filaments at Recombination, the subsequent contractions that undoubtedly took place can account for this amplification very easily, only involving two or three orders of magnitude.

b) If magnetic fields are generated via battery processes similar to Biermann's, in the galactic formation itself, then magnetic fields would only be present inside galaxies or in their close vicinity. However, as mentioned above, strong magnetic fields have been observed in the intracluster and in the intercluster media.

Next Contents Previous