


Coles (1992) suggested that the failure of CDM models to explain large scale structures could be satisfactorily surmounted if magnetic fields were taken into account. Large scale structures are characterized by a noticeable regularity and periodicity (Broadhurst et al., 1990; Einasto et al. 1994; Tucker et al. 1997; Landy et al. 1996; Quashnock et al. 1996; Atrio-Barandela et al. 1997; Tully et al. 1992; Einasto et al. 1997a, b, c; Retzlaff, 1998; Tadros et al. 1998, Toomet et al., 1999, and others) suggesting a network of filaments.
Battaner, Florido and Jimenez-Vicente (1997), Florido and Battaner (1997), Battaner, Florido and Garcia-Ruiz (1997), Battaner and Florido (1998) and Battaner (1998) have theoretically analyzed the influence of magnetic fields on the large scale structure along the radiation dominated universe and their conclusions may be summarized as follows:
a) Preexisting magnetic fields are able to produce anisotropic density inhomogeneities in the photon fluid and local metric perturbations. In particular, they are able to produce filamentary structures in the distribution of the energy density.
b) Particularly interesting are those filaments larger than about
![]() 10 Mpc, because they have no problems with magnetic
diffusion (as
mentioned above), because their evolution is more predictable and
because they can be observed today. In fact these radiative and
gravitational potential filaments were the sites where baryons, or any
other dark matter component, collapsed at Recombination, forming the
illuminated supercluster filaments that are observed today as elements
of the
large scale structure. Non linear effects have very much distorted the
pre-Recombination structures, as well as the larger ones, though to a
much lesser extent, as
10 Mpc, because they have no problems with magnetic
diffusion (as
mentioned above), because their evolution is more predictable and
because they can be observed today. In fact these radiative and
gravitational potential filaments were the sites where baryons, or any
other dark matter component, collapsed at Recombination, forming the
illuminated supercluster filaments that are observed today as elements
of the
large scale structure. Non linear effects have very much distorted the
pre-Recombination structures, as well as the larger ones, though to a
much lesser extent, as
![]()
![]() /
/![]() remains low. Therefore, these
pre-Recombination radiative filaments should be identifiable today.
remains low. Therefore, these
pre-Recombination radiative filaments should be identifiable today.
c) The orders of magnitude of these magnetic fields are equivalent to
present
B0 ![]() 10-8 - 10-9G. If they were much
lower, they
would have no influence on the larger scale structure. If they were much
higher, the
formation of the galaxy would have taken place much earlier.
10-8 - 10-9G. If they were much
lower, they
would have no influence on the larger scale structure. If they were much
higher, the
formation of the galaxy would have taken place much earlier.
d) The filament network, if magnetic in origin, must be subject to some magnetic restrictions. The simplest lattice matching these restrictions is an "egg-carton" network, formed by octahedra joining at their vertexes. This "egg-carton" universe would have larger amounts of matter along the edges of the octahedra, which would be the sites of the superclusters. Outside the filaments there would be large voids, devoid not only of baryons but also of magnetic fields (Fig. 21). Magnetic field lines would be concentrated in the filaments, with their directions being coincident with those of the filaments.

|
Figure 21. Ideal scheme of the egg-carton universe formed with octohedra only contacting at their vertexes. Adopted from Battaner and Florido (1997). Courtesy of Astronomy and Astrophysics. |
These theoretical speculations are compatible with present observations of the large scale structure as delineated by the distribution of superclusters. It is easy to identify at least four of these giant octahedra in real data, which comprise observational support for the egg-carton universe. Two of them, those which are closest and therefore most unambiguously identified, are reproduced in Fig. 22. Nearly all the important superclusters in the catalogue by Einasto et al (1997), as well as nearly all the important voids in the catalogue by Einasto et al. (1994) can be located within the octahedron structure. This web is slightly distorted by the presence of the very massive Piscis-Cetus supercluster in one of the filaments.
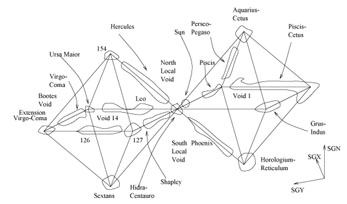
|
Figure 22. The two large octahedra closer to the Milky Way. |
The magnetic origin of structures at very large scales alleviates the old problem encountered by CDM models which predict too little structure at large scales (see, for instance, the reviews by Bertschinger, 1998 and Ostriker, 1993).
A fractal nature could be compatible with the octahedron web, in agreement with the identification of fractals by Lindner et al. (1996) from the observational point of view. There could be sub-octahedra within octahedra, at least in a limited range of length scales. The simplest possibility is reproduced in Fig. 23 in which 7 small octahedra contacting at their vertexes have their egg-carton structure within a large octahedron, the ratio of large/small octahedron size being equal to 3. The fractal dimension becomes quantified, with 1.77 and 2 being the most plausible values. The scale of the fractal structure would range from 150 Mpc, i.e. slightly lower than the deepest surveys, down to about 10 Mpc (in agreement with Lindner et al), as shorter scale magnetic fields would have been destroyed by the resistive radiation dominated universe. Whether the fractal egg-carton structure continues indefinitely for larger scales as suggested by Sylos Labini et al. (1998) and others, remains an open question, but Battaner (1998) proposed this structure under the adoption of the Homogeneity Cosmological Principle at large enough scales.

|
Figure 23. Ideal scheme of the fractal geometry of the octahedron network. In this figure we plot the case of a fractal dimension equal to 1.77. A value of 2 is also an interesting possibility. Adopted from Battaner (1998). Courtesy of Astronomy and Astrophysics. |
The absence of a relation between Faraday rotation and redshift of
quasars indicates that a widespread cosmological aligned magnetic field
must be
B0 < 10-11G
(Lesch and Chiba, 1997;
Kronberg, 1994;
Rees and Reinhardt, 1972;
Kronberg and Simard-Normandin,
1976;
Vallée, 1983,
1990).
However, the distribution of large scale magnetic fields
is probably very far from homogeneous. Not only < ![]() > = 0, but < B2 >, even if
not vanishing, is far from homogeneous. Instead, we are interested in
the peak values to be found in the matter filaments, in which case
this limit should be increased by a large
factor, even if it is very low in voids, i.e. in the largest
fraction of the volume of the Universe.
> = 0, but < B2 >, even if
not vanishing, is far from homogeneous. Instead, we are interested in
the peak values to be found in the matter filaments, in which case
this limit should be increased by a large
factor, even if it is very low in voids, i.e. in the largest
fraction of the volume of the Universe.
There are other upper limits that should be increased by this factor too, if we are interested in the field strength within the filaments: for instance, B0 < 10-7G, taking into account the 4He abundance (Greenstein, 1969; Zeldovich and Novikov, 1975; Barrow, 1976; Cheng, Schramm and Truran, 1994; Matese and O'Connell, 1970; Grasso and Rubinstein, 1995, 1996 and others), B0 < 4 × 10-9G, taking into account the neutrino spin flip (though very much depending on the mass of all neutrinos) (Shapiro and Wasserman, 1981; Enqvist et al., 1993), and B0 < 4 × 10-9G, based on the CMB isotropy (Lesch and Chiba, 1997; Barrow, 1976; Barrow, Ferreira and Silk, 1997).
Observations of the distribution and orientation of warps of galactic disks, under the interpretation that these warps are produced by intergalactic magnetic fields (Battaner et al. 1991; Battaner, Florido and Sanchez-Saavedra, 1990; Zurita and Battaner, 1997) show coherence regions of about 25 Mpc, though Vallée (1991) did not confirm this coherent orientation. In any case, the volume of observed galaxies is too small compared with the scales we are now considering.
The improved sensitivity of experiments intended to measure the CMB would
permit us to gather direct information about large scale magnetic fields
(Magueijo, 1994;
Kosowsky and Loeb, 1997;
Adams et al., 1996,
and others).Ultrahigh energy cosmic rays can also observe valuable
information (e.g.
Lee, Olinto and Siegl, 1995;
Stanev et al., 1995;
Stanev, 1997
and others), as well as the delay in
the arrival of the energetic TeV-![]() -rays with respect to the
low-energy-
-rays with respect to the
low-energy-![]() -rays
(Plaga, 1995).
-rays
(Plaga, 1995).