Published in "The Central kpc of Starburtsts and AGN",
ASP Conference Series, Vol. xxx, 2001, eds. J. H. Knapen, J. E. Beckman,
I. Shlosman, and T. J. Mahoney;
0106436
GLOBAL VERSUS NUCLEAR STARBURSTS
Françoise Combes
DEMIRM,
Observatoire de Paris,
61 Av. de l'Observatoire, F-75 014, Paris, France
Abstract.
The strongest starbursts are observed towards galaxy nuclei,
or circumnuclear regions. However in interacting galaxies,
star formation is also triggered in overlap regions far from
nuclei, in spiral arms and sometimes in tidal tails.
What is the relative importance of these starbursts?
What kind of starformation is dominating, as a function of redshift?
These different starbursts occur in different dynamical
conditions (global and local): gravitational instabilities,
density waves, radial flows, shear, cloud collisions, density accumulations,
and they have been investigated with the help of numerical simulations.
Gravitational instabilities are necessary to initiate star formation,
but they
are not sufficient; galactic disks are self-regulated through these
instabilities
to have their Toomre Q parameter of the order of 1, and thus this criterium
is in practice unable to predict the onset of intense star formation.
Super star clusters are a characteristic SF mode in starbursts, and
might be due to the rapid formation of large gas complexes.
Star formation can propagate radially inwards, due to gravity torques
and gas inflow, but also outwards, due to superwinds, and energy outflows:
both expanding or collapsing waves are observed in circumnuclear regions.
Mergers are more efficient in forming stars at high redshift, because
of larger gas content, and shorter dynamical times.
The relation between nuclear starbursts and nuclear activity
is based on the same fueling mechanisms, but also on
reciprocal triggering and regulations.
 OBSERVATIONS : WHERE ARE STARBURSTS LOCATED ?
OBSERVATIONS : WHERE ARE STARBURSTS LOCATED ?
 DYNAMICAL MECHANISMS
DYNAMICAL MECHANISMS
 Global statistical studies
Global statistical studies
 Parameters governing the SFR
Parameters governing the SFR
 Why are Q and
Why are Q and
 c
actually not
very useful to predict star formation trigger and starburst activity?
c
actually not
very useful to predict star formation trigger and starburst activity?
 Influence of bars
Influence of bars
 LARGE GAS COMPLEXES AND STELLAR CLUSTERS
LARGE GAS COMPLEXES AND STELLAR CLUSTERS
 FEEDBACK, REGULATION, PROPAGATION
FEEDBACK, REGULATION, PROPAGATION
 STARBURSTS AS A FUNCTION OF REDSHIFT
STARBURSTS AS A FUNCTION OF REDSHIFT
 More efficient star formation at high z
More efficient star formation at high z
 Relation between starburst and AGN
Relation between starburst and AGN
 CONCLUSIONS
CONCLUSIONS
 REFERENCES
REFERENCES
1. OBSERVATIONS : WHERE ARE STARBURSTS LOCATED ?
It is a widely observed fact that starbursts are concentrated
in nuclei, and in particular the strongest ones (ULIRGs).
But there can be exceptions, such as:
- the Antennae, Arp 299, where star formation
is more intense in overlap regions between the two galaxies,
- in bright spiral arms (like M51, etc..)
- the Cartwheel and other collisional ring galaxies: the starburst occurs
in the ring, sometimes in the nucleus, or toward the second developing ring,
- in nuclear resonant rings of barred galaxies; this ring might shrink
with time
and the starburst drifts towards the center, as seems to be the case in
M82 : a fossil region M82B NE
(de Grijs et al 2001),
has been studied 1kpc from the central nuclear starburst.
M82 is a good opportunity to study the evolution of
starburst location:
in the M82B fossil region (see figure 1), stars
formed 100 Myr ago, with a comparable amplitude than the present starburst
in the center.
De Grijs et al. (2001)
find there an important (113) number of
evolved super star clusters (SSC). Their detailed age study conclude
that the
starburst begun 2 Gyr ago, with a peak 600 Myr ago, and stopped about
30Myr from now. This episode could coincide to a previous
passage/interaction of the companion M81. The evolution of the SSCs
is compatible with them being progenitors of globular clusters.
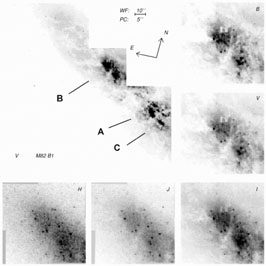
|
Figure 1. HST-WFPC2 image (V-band) of M82
(in the center), and
PC-field images in B, V, I and NICMOS in J & H, from
de Grijs et al. (2001).
The PC and NICMOS images are centered on the fossil starburst
(region B), while regions A and C indicate the present on-going
nuclear starburst. In M82B, a large system of evolved super star clusters
has been found.
|
This evolution of the starburst location could correspond
to ring concentration and ring evolution. Indeed, in
barred galaxies star formation is frequently in nuclear rings (cf
Buta et al 2000,
NGC 1326;
Maoz et al 2000,
NGC 1512, NGC 5248), and in particular bright knots in the rings.
Sometimes star formation can occur even farther
from the center: in tidal dwarfs (e.g.
Duc et al. 2000),
shells, garlands, large HII complexes in the outer regions, as in M101
or NGC 628
(Lelièvre & Roy
2000).
Or the nucleus does not concentrate the star formation activity,
which is more randomly distributed, as in dwarf irregulars.
A recently studied example is NGC 4214
(Beck et al. 2000;
MacKenty et al. 2000),
where interferometric CO observations
(Walter et al 2001)
reveal that the star formation is not always coinciding with the
gaseous concentrations. If one CO complex is indeed the site
of a starburst, a comparable one, at the same distance from the
center, is completely quiecent.
An interesting question is to estimate the relative importance
of starburst, and more quiescent or "steady-state" star formation
in the global rate of star formation of the Universe.
If a starburst is defined as having a rate larger than 50
M /yr,
an estimation from NICMOS images in the Hubble Deep Field
conclude that both processus appear similar in importance
(Thompson 2000).
/yr,
an estimation from NICMOS images in the Hubble Deep Field
conclude that both processus appear similar in importance
(Thompson 2000).
2. DYNAMICAL MECHANISMS
Since the fuel for star formation is the interstellar gas, it is
straightforward to assume that the star formation rate should
be proportional to some power of the volumic gas density in galaxies,
as done by
Schmidt (1959).
Following this assumption, Schmidt
derived that this power should be around
n = 2 (1) in the solar
neighborhood.
However, this local hypothesis has revealed very difficult to confirm,
although
there is of course some correlations between global gas density
and star formation rate in a Galaxy. The difficulty is certainly
related to the time delays and time-scales for star formation processes
and subsequent feedback, and also to the fact that the gas can be
stabilised by dynamical mechanisms, instead of forming stars.
2.1. Global statistical studies
So far, only global quantities have been correlated
with success, when the gas surface density is averaged
out over the whole galaxy, and the same for the star formation rate.
The star formation tracer can vary, from the
H flux
for normal galaxies, to the Far Infrared luminosity L(FIR) for
starbursts, which are highly obscured
(Kennicutt 1998).
flux
for normal galaxies, to the Far Infrared luminosity L(FIR) for
starbursts, which are highly obscured
(Kennicutt 1998).
While the starbursts explore a wider range and dynamics
of parameters, the relation between
the global gas surface density and star formation rate (SFR)
is the same for extreme and normal galaxies: it is possible
to derive a "global" Schmidt law, with a power n = 1.4
(Kennicutt 1998).
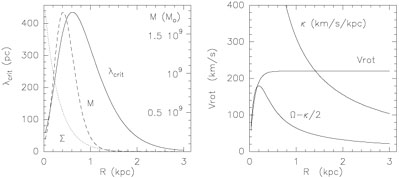
(cf figure 2). Another formulation works as well
where  is the angular
frequency in the galaxy, which is
inversely proportional to the dynamical time-scale tdyn.
is the angular
frequency in the galaxy, which is
inversely proportional to the dynamical time-scale tdyn.
Several justifications can be found a posteriori: if the star formation
is locally due to the gravitational instability of the gas, this occurs on
a free-fall time-scale, and the star-formation rate is:
very close to the power n = 1.4; but the correlation is not observed
locally. Globally, this applies also, if the star formation is due to
the global gravitational instability of the gas disk, that occurs in a
dynamical time-scale:
which accounts for the second formulation. Alternatively, star formation
could be triggered in marginally stable clouds, by the crossing of
spiral arms, and the frequency of arm crossing is
proportional to  -
-
 p
(Wyse & Silk 1989),
or roughly to
p
(Wyse & Silk 1989),
or roughly to  far from
corotation (where the clouds never cross the arms).
far from
corotation (where the clouds never cross the arms).
This second formulation might also explain the Tully Fisher relation
(Silk, 1997;
Tan 2000),
since if  SFR
SFR

 gas
gas
 , then
, then
with vcirc2

 R from the virial, and
provided that
R from the virial, and
provided that  gas
gas

 * is
verified over the main spiral classes
(Roberts & Haynes
1994),
it can be deduced that Lb
* is
verified over the main spiral classes
(Roberts & Haynes
1994),
it can be deduced that Lb
 vcirc3.
vcirc3.
The numerical values found for the global Schmidt law correspond
to an SFR of 10% of gas per orbit transformed into stars,
at the outer edge typically for normal galaxies.
The much higher SFR in starbursts could be only a consequence of their much
higher surface density: indeed
 gas is observed
to be 100 to 10 000 higher, and the star formation efficiencies (SFE)
about 6-40 times higher.
This higher efficiency can also be attributed to
smaller dynamical time-scales, since starbursts usually happen in
nuclear regions.
gas is observed
to be 100 to 10 000 higher, and the star formation efficiencies (SFE)
about 6-40 times higher.
This higher efficiency can also be attributed to
smaller dynamical time-scales, since starbursts usually happen in
nuclear regions.
A starburst is obtained as soon as dynamical mechanisms have brought
gas to the center; this can occur through gravity torques on dynamical
time-scales. The gas infall must be sufficiently rapid to overcome the
feedback processes, that will blow the gas out. These processes, such
as supernovae explosions and violent stellar winds, occur on time-scales
of 107 yr, the life-time of O-B stars. The latter is
unchanged at any galactic
radius, being intrinsic to stellar physics. Only in nuclei dynamical
torques can bring the gas faster than these feedback mechanisms.
The global statistical studies appear to be slightly different for extreme
starbursts
(Taniguchi & Ohyama
1998).
The exponent of the global Schmidt law is more near n = 1, and
 SFR
SFR

 gas (cf also
Young et al 1986).
As for radial distribution, there is no correlation between
gas (cf also
Young et al 1986).
As for radial distribution, there is no correlation between
 FIR and
FIR and
 gas.
It is the total gas amount of a galaxy that governs the infrared
luminosity L(FIR).
gas.
It is the total gas amount of a galaxy that governs the infrared
luminosity L(FIR).
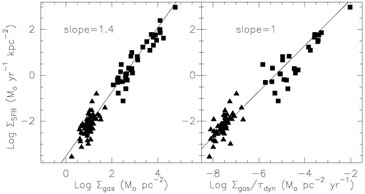
|
Figure 2. Relations between Star Formation
Rate (SFR) and gas surface densities, from
Kennicutt (1998).
Left: a global "Schmidt" law,
with a slope of n = 1.4 as the best fit. Right: linear relation
between SFR and gas over dynamical time (
 dyn) ratio. Normal
galaxies are the
triangles, while starburst galaxies are the squares. dyn) ratio. Normal
galaxies are the
triangles, while starburst galaxies are the squares.
|
2.2. Parameters governing the SFR
The difficulty is that there are many physical parameters determining
the SFR and SFE in galaxy disks. Along the Hubble sequence, the star
formation rate increases towards late-type, wich could be due
to dynamical instability increasing with decreasing bulge-to-disk ratio.
The SFE has been found to decrease with size
(Young 1999).
However, this could be due to a metallicity effect, since SFE is
computed from the infrared to H2 ratio, SFE = L(FIR) /
M(H2), itself derived
from L(FIR) / L(CO), and L(CO) could lead to an underestimation
of H2 in low-mass under-abundant galaxies.
The SFR also depends on environment, since galaxy interactions
are one of the most widely recognized trigger of starbursts.
Gravity torques are also essential for radial gas flows, and
thus the bar phase or chronology might play a role, as well as the gas
content.
The most essential physical parameters are :
- Gravitational instability, the main trigger of star formation;
this might explain the existence of a threshold of gas density for star
formation, the critical surface density
 c
(Quirk 1972,
Kennicutt 1989);
c
(Quirk 1972,
Kennicutt 1989);
- Cloud-cloud collisions, a process also
proportional to a power of local volumic density,

 2,
that could imply a local Schmidt law. It is possible to account for
observations of SFR and SFE, by considering only collisions
(Scoville 2000,
Tan 2000);
2,
that could imply a local Schmidt law. It is possible to account for
observations of SFR and SFE, by considering only collisions
(Scoville 2000,
Tan 2000);
- Tidal forces;
interaction and mergers are the main trigger of starbursts (e.g.
Kennicutt et al. 1987,
Sanders & Mirabel
1996).
Also, after the interaction, the binary black hole thus formed
can trigger a starburst by its dynamical perturbations
(Taniguchi & Wada
1996);
- Gas density
(Schmidt 1959,
Kennicutt 1998),
and radial gas flows due to gravity torques (bars);
- Supernovae/winds can also drive star formation
(Wada & Norman, 1999,
2001);
clouds marginally stable could be
driven into gravitational instability by an
excess of pressure, a blast wave
(Koo & McKee 1992,
Heckman et al 1996,
Taniguchi et al 1998).
Star formation can be contagious, since
it propagates local instabilities.
Since all these phenomena play a role in the star formation, a
global Schmidt law, averaged over the whole galaxy, is not sufficient to
disentangle the relative importance of each process.
In particular, local studies reveal that the
gas density alone is not a sufficient parameter to predict SFR and SFE
(cf gas concentrations without starbursts,
Jogee & Kenney 2000).
It is tempting to test the stability of gaseous disks, with the Toomre
criterium Q (and its equivalent formulation as a critical gas density
 c),
in order to explain the occurence of star formation in special regions
or galaxies. However in a dynamical time, gravitational instabilities
are able to heat a disk until the stability criterium is verified in
almost all disks, and external parameters are not included in the
criterium.
c),
in order to explain the occurence of star formation in special regions
or galaxies. However in a dynamical time, gravitational instabilities
are able to heat a disk until the stability criterium is verified in
almost all disks, and external parameters are not included in the
criterium.
2.3. Why are Q and
 cactually not
very useful to predict star formation trigger and starburst
activity?
cactually not
very useful to predict star formation trigger and starburst
activity?
The main problem is that the criterium for gravitational instabilities
is often undissociated from the criterium of star formation.
But in reality, if gravitational instabilities are necessary for
star formation, they are not sufficient. There are still some
other parameters that are essential, controlling the onset of
star formation in a gas medium that has formed self-gravitating
structures, and those parameters are still to be sorted out and
quantified to build a criterium for star formation:
1) Self-regulation
Gravitational instabilities are so important that disks are
self-regulated to have the Toomre Q parameter of the order of 1.
Indeed, as soon as Q falls below 1 because of gas dissipation,
the disk becomes gravitationnally unstable: these instabilities
have for immediate effect to increase the velocity dispersion,
and heat the disk so that Q ~ O(1) again (e.g.
Lin & Pringle 1987).
But this self-gravitating process occurs even in the absence of
star formation, so that Q ~ O(1) in any disk and cannot help
to predict star formation.
For instance, in the outer parts of spiral disks, where it is obvious
that there is no star formation at all, the HI gas is observed to be
gravitationally unstable and form structures at all scales: there are
spiral arms, giant clumps, and a mass spectrum of clouds
(structures down to the smallest structure possible to see with the present
21cm beams). It is therefore likely that Q is also there of the order
of 1, and the disk self-regulated.
This occurs also inside some irregular galaxies, possessing a lot of gas,
without star forming activity like N2915
(Bureau et al 1999).
The gas has developped gravitational instabilities, spiral arms, etc..
2) Multi-phase gas and multi-components stability
Let us emphasize that Q and
 c characterizing
the stability of disks, should be computed taking into account
all components, gas and stars, and in case of several gas components,
the total multi-phase medium. This is not possible analytically, since
the different components have not the same velocity dispersion, but an
empirical criterium has been proposed as:
c characterizing
the stability of disks, should be computed taking into account
all components, gas and stars, and in case of several gas components,
the total multi-phase medium. This is not possible analytically, since
the different components have not the same velocity dispersion, but an
empirical criterium has been proposed as:
(Jog 1992).
Therefore, each component has a weight

 /
/
 in the stability.
When there is a large surface density of gas, the Qgas term
dominates, and it is justified to compute Q and
in the stability.
When there is a large surface density of gas, the Qgas term
dominates, and it is justified to compute Q and
 c taking
gas only into consideration. But as soon as the gas surface density
is depleted for some reason (for instance inside circum-nuclear rings),
or the gas is heated
(
c taking
gas only into consideration. But as soon as the gas surface density
is depleted for some reason (for instance inside circum-nuclear rings),
or the gas is heated
( gas increases),
then the Qstar
term has to be taken into account, ensuring that the total Q is always
of the order of 1, over the whole disk (e.g.
Bottema 1993).
As for the gas velocity dispersion, when there exist
non-axisymmetric features, like spiral arms, bars, etc .. the corresponding
streaming motions have to be included in
gas increases),
then the Qstar
term has to be taken into account, ensuring that the total Q is always
of the order of 1, over the whole disk (e.g.
Bottema 1993).
As for the gas velocity dispersion, when there exist
non-axisymmetric features, like spiral arms, bars, etc .. the corresponding
streaming motions have to be included in
 gas (which does
not reduce to the local sound speed velocity of the order of 10km/s),
since it is precisely these streaming motions that are the consequences
of disk heating by spiral waves and gravitational instabilities.
gas (which does
not reduce to the local sound speed velocity of the order of 10km/s),
since it is precisely these streaming motions that are the consequences
of disk heating by spiral waves and gravitational instabilities.
3) Spatial averaging scale
A problem in estimating Q and
 c is also the
scale at which they
are averaged, and the results can change completely according to the
spatial resolution of the observations.
We know that the interstellar medium is fractal and possess structures
at all scales,
from 100 pc to ~ 10 AU. The gas surface density increases towards
small scales, by about 1-2 orders of magnitude; the critical surface density
might be reached or not, according to the spatial scale of averaging
(Klessen 1997;
Wada & Norman 1999,
2001;
Semelin & Combes 2000;
Huber & Pfenniger
2001).
c is also the
scale at which they
are averaged, and the results can change completely according to the
spatial resolution of the observations.
We know that the interstellar medium is fractal and possess structures
at all scales,
from 100 pc to ~ 10 AU. The gas surface density increases towards
small scales, by about 1-2 orders of magnitude; the critical surface density
might be reached or not, according to the spatial scale of averaging
(Klessen 1997;
Wada & Norman 1999,
2001;
Semelin & Combes 2000;
Huber & Pfenniger
2001).
4) Uncertainty on the H2 gas density
The biggest uncertainty in computing the gas surface density is
the CO to N(H2) conversion ratio. This ratio can vary within
a factor 2 or 10, according to metallicity, CO excitation, temperature,
density, etc ..
(Rubio et al 1993,
Taylor et al 1998,
Combes 2000),
and since Q ~ O(1) in galaxy disks
anyway, it is quite impossible to ascertain that Q is larger or smaller
than 1 if such systematic uncertainties are
attributed to the gas density. Due to the latter,
it is likely that systematics will find
 gas <
gas <
 c
for non-star forming regions, where the CO is not excited (or the
metallicity not enough), and
c
for non-star forming regions, where the CO is not excited (or the
metallicity not enough), and
 gas >
gas >
 c for starbursts
(12C is a
primary element, and the abundance of CO is enhanced in starbursts).
c for starbursts
(12C is a
primary element, and the abundance of CO is enhanced in starbursts).
5) Intermittency
Star formation can be inhibited or triggered by other phenomena, such as
supernovae, stellar winds, external or internal wave triggers and this does
not enter the Q and
 c estimations. In
a nuclear disk, simulations by
Wada & Norman (2001),
the density undergoes phases of episodic
and recurrent star formation (of the order of ~ 10 Myr periodicity),
and the estimation of
c estimations. In
a nuclear disk, simulations by
Wada & Norman (2001),
the density undergoes phases of episodic
and recurrent star formation (of the order of ~ 10 Myr periodicity),
and the estimation of
 c are the same
for periods with and
without star formation. Here is introduced a hidden parameter, which
is the past history of star formation. A galactic disk region might be
quiescent, only in between two star formation phases for instance.
c are the same
for periods with and
without star formation. Here is introduced a hidden parameter, which
is the past history of star formation. A galactic disk region might be
quiescent, only in between two star formation phases for instance.
In conclusion, gravitational instabilities ensure that all spiral disks have
Q ~ O(1) at all radii: the gas component is structured in clouds that
are marginally stable. Only transiently the disk can be brought out of
equilibrium. Only a sudden trigger is necessary to start a
starburst, and these are difficult to recognize. This could be a sudden
radial gas flow due to a bar, or the tidal action of a companion, that
strengthens or creates a bar, that will bring gas to the nucleus,
when the dynamical time-scale is short.
To have a starburst, gas must be gathered in a very short time-scale,
smaller
than ~ 107 yr, shorter than the onset of feedback from the first
OB stars formed, through supernovae explosions and stellar winds, before
the starburst can blow the gas out.
In nuclei, the dynamical time-scale is shorter, while the feedback
time-scale is constant all over the disk (being intrinsic to the
life-time of OB stars).
That might explain why starbursts are always more conspicuous in nuclei.
The original Schmidt law is a local one, and involves the volumic density
 . At this stage,
one should consider that the surface density in inner and outer
parts of the galaxies have not the same weight for gravitational
instabilities, because of the flaring of gas and star densities towards
the outer parts.
. At this stage,
one should consider that the surface density in inner and outer
parts of the galaxies have not the same weight for gravitational
instabilities, because of the flaring of gas and star densities towards
the outer parts.
2.4. Influence of bars
It was found, with IRAS fluxes as a tracer of star formation, that
barred galaxies were more frequently starbursting
(Hawarden et al. 1986),
and had also
more radio-continuum central emission, attributed to star formation
(Puxley et al. 1988).
From a statistical sample of more than 200 starbursts and normal galaxies,
Arsenault (1989)
found a much larger frequency of barred and
ringed types among the starbursts, suggesting
that active formation of stars in the nuclei of spirals is
linked to the perturbation of bars and gravity torques.
But such a correlation is not without any controversy:
Pompea & Rieke (1990)
do not find that strong bars appear
an absolute requirement for high infrared luminosity in isolated galaxies.
Markarian starbursting galaxies are less barred than a sample of normal
galaxies
(Coziol et al. 2000).
At least the molecular gas appears much more concentrated in barred galaxies
(Sakamoto et al 1999),
which is expected form gravity torques.
This gas concentration should trigger nuclear starbursts, according
to the Schmidt law.
As for nuclear activity itself, the correlation between the presence
of bars and AGN activity is presently unclear, as described already in this
conference.
Peletier et al (1999)
and Knapen et al (2000)
have shown that Seyferts have more bars than normal galaxies
(results at 2.5 ).
Seyferts have curiously a lower fraction of strong bars
(Shlosman et al 2000),
perhaps pointing toward
the destruction of bars by massive black holes.
Besides, Seyferts have more outer rings, by a factor 3 or 4
(Hunt & Malkan 1999).
Since the outer rings are the vestiges of
the action of bars, this supports the scenario of bar destruction by
central gas accretion and massive black holes.
).
Seyferts have curiously a lower fraction of strong bars
(Shlosman et al 2000),
perhaps pointing toward
the destruction of bars by massive black holes.
Besides, Seyferts have more outer rings, by a factor 3 or 4
(Hunt & Malkan 1999).
Since the outer rings are the vestiges of
the action of bars, this supports the scenario of bar destruction by
central gas accretion and massive black holes.
An interesting feature recently discovered in stellar kinematics
of star-forming galaxies with an active nucleus, is the drop in velocity
dispersion in the central kpc. This was found thanks to ISAAC on the VLT
(Emsellem et al 2001,
and this conference). This drop is unexpected, especially since the
dispersion should increase towards the massive black hole. But the
phenomenon can be transient, and due to kinematically cold stars just
formed from the gas in the nuclear disk fueled by the bar torques.
As for numerical simulations, starbursts are easily reproduced,
in particular triggered by galaxy interactions and mergers. The
star-formation
is due to radial gas flows, driven by the bars formed in the interaction
(e.g.
Mihos & Hernquist
1994,
1996;
Bekki 1999).
The bar is thus central to
the starburst. The presence of a bulge, which has a
stabilising influence on disks against bar formation, is determinant
in the occurence of the starburst. In galaxies with a large bulge-to-disk
ratio, the intense starburst has to wait the merging, and the final
gas infall, while galaxies without large bulges undergo
repetitive starbursts.
Other dynamical perturbations, like lopsidedness and m = 1 waves
are also triggering starbursts: in this case, star formation is mainly
in the disk, and not boosted in the nucleus
(Rudnick et al 2000).
1 Schmidt compared the scale-height of
the galactic plane in gas and young stars to derive this power, and
found a high value because the molecular hydrogen distribution
was not known at that time
Back.
3. LARGE GAS COMPLEXES AND STELLAR CLUSTERS
Due to the large gas surface density in nuclear
starbursts, the critical length for self-gravity in the disk center
(the scale with the largest growth rate) is also very large:
where  ~
~
 gas, since the gas
is dominating there. The corresponding self-gravitating mass is
gas, since the gas
is dominating there. The corresponding self-gravitating mass is
 2
2
 , or
, or

 3.
Figure 3 gives orders of magnitude for these values,
typical sizes and masses 200 pc, 109
M
3.
Figure 3 gives orders of magnitude for these values,
typical sizes and masses 200 pc, 109
M .
.
These super complexes will collapse, and may form
super star clusters, if another factor is tuned,
the time-scale before feedback effects
come into play, and regulate the star formation.
The collapse of gas must be sudden enough
(in < 10 Myr), so that OB stars and SN cannot limit
the process. This means that the free-fall time is short
enough, and therefore that the volumic density is larger
than 2 M /
pc3. This is indeed verified for the
typical masses and sizes determined above, but not for usual giant
molecular clouds.
/
pc3. This is indeed verified for the
typical masses and sizes determined above, but not for usual giant
molecular clouds.
Another point of view to see the
formation of these large complexes, is to introduce the velocity dispersion
(Elmegreen et al. 1993).
In interacting and merging galaxies, one
characteristic is that the tidal perturbations have increased
velocity dispersion above that of a quiescent disk, and
the corresponding pressure stabilises locally the gas up to a larger
Jeans length. The complexes that form are then bigger.
The largest growth rate for instabilities in the disk occurs at
the scale  crit
considered above, which is also equal to the Jeans length:
crit
considered above, which is also equal to the Jeans length:
since the Toomre parameter Q
~ 
 /
/
 G
G
 ~ 1.
In fact, the kinetic pressure stabilises all scales below Jeans length,
and the galactic rotation stabilises all scales above
~ 1.
In fact, the kinetic pressure stabilises all scales below Jeans length,
and the galactic rotation stabilises all scales above
 crit,
the equality between the two ensuring the disk stability. If the disk
is slightly out of equilibrium, it is those common scales that are
unstable more quickly.
crit,
the equality between the two ensuring the disk stability. If the disk
is slightly out of equilibrium, it is those common scales that are
unstable more quickly.
With this second formulation, the mass of the complexes are
proportional to
 4 /
4 /
 , and grow at a rate
, and grow at a rate
 ff =
ff =
 /
/
 showing the large importance of velocity dispersion.
showing the large importance of velocity dispersion.
Super Star Clusters (SSC) are
young star clusters of extraordinary luminosity and compactness.
They are one of the dominant modes of star formation in starbursts, and they
are thought to be a formation mechanism for globular clusters.
A major breakthrough from HST has been to show that
globular clusters form still at the present time, through starbursts (e.g.
Schweizer 2001).
The question has been raised of the SSC contribution to the total
luminosity: it appears only moderate in ULIRGs
(Surace et al 1998).
In Arp 220 for example
(Shioya et al 2001),
there are three conspicuous nuclear SSC (galactic radius < 0.5kpc),
which correspond to about 0.2 Ltot (they are
heavily obscured > 10 mag). The
disk SSC (0.5 < radius < 2.5 kpc), of lower luminosity,
represent a negligible contribution.
SSC also form in starbursting dwarfs, with properties
quite similar to larger interacting/merging galaxies (e.g
Telles 2001).
In these systems, they could represent a significant part of the
luminosity. Their formation is thought to be triggered by the high pressure
experienced by the gas complexes in a starburst environment.
4. FEEDBACK, REGULATION, PROPAGATION
The study of stellar populations, through multiband photometry
and spectroscopy, together with HII regions
and molecular gas distribution, and assisted by starburst
evolutionary models, leads to the determination of the age
and history of the star formation in a galaxy disk.
It is possible to constrain the IMF, often found to be
biased towards high-masses in starbursts, and to follow the
propagation of the starburst radially.
In some cases, the star formation propagates
inside out, a good example being the ring of NGC 1614
(Alonso-Herrero et al
2001):
here a nuclear starburst is
identified within 45pc, surrounded by a ring of HII regions
of 600 pc in diameter, tracing a younger burst.
These HII regions, about 10 times the intensity of 30 Doradus,
lie inside a ring of molecular gas, as if the star formation
wave was propagating radially outwards.
In the LINER galaxy NGC 5005,
Sakamoto et al (2000)
identify a stream of molecular gas, linking the inner ring
of the bar to the nuclear disk, likely to correspond to the ILR.
This stream represents a high rate of bar-driven inflow and
they suggest that a major fueling event is in progress in
this galaxy. The gas flow could then be episodic rather than continuous.
Recurrent starbursts are then expected.
In other cases, the star formation appears to propagate
outside in: older star formation in a disk/ring of 200pc
in diameter surrounds a younger nuclear starburst in NGC 6764
(Schinnerer et al 2000):
two starbursts with decay times of 3 Myr occurred 3-5 Myr and 15 to 50
Myr ago. However, a constant star formation scenario over 1 Gyr
(at a rate of 0.3 M / yr) could also explain the data.
/ yr) could also explain the data.
The ringed barred galaxy NGC 4314 also supports the outside in scenario:
a ring of dense molecular gas is observed inside the radio-continuum ring
(Combes et al 1992;
Benedict et al 1996;
Kenney et al 1998).
The gas ring, inside the nuclear hot spots, evolves slowly, reducing
its radius due to friction exerted by the background stars on the
giant molecular clouds.
This shrinking ring of star formation
is expected from the dynamical evolution of the gaseous nuclear ring.
Alternatively, feedback processes from violent star formation,
such as supernovae, bipolar gas outflows, etc ... are expected to compress
the surrounding gas outwards, and to trigger star formation inside out.
5. STARBURSTS AS A FUNCTION OF REDSHIFT
5.1. More efficient star formation at high z
It is now widely recognized that starbursts were
more frequent in the past, and galaxy imaging at
high redshift with the Hubble Space Telescope has revealed
considerable evolution. Although there are still many
systematic biases in high-z studies, it appears that
galaxies were more numerous, and in particular
more perturbed and irregular. The Hubble classification is
difficult to pursue at high z. Galaxies are knotty, have
less organised structures, and much less bars
(van den Bergh et al
2001).
Their irregular appearance can be attributed to interactions, since
there are more pairs and more mergers at high redshift
(Lefevre et al 2000).
The higher star formation rate at high z is easy to explain :
- More gas at high redshift
- Higher interaction and merging rates
- Dynamical time shorter (to accrete gas)
In the frame of the hierarchical scenario, where large galaxies
today have been formed by succesive mergers of smaller entities,
the first haloes to form at high redshift have very small masses.
But they are also denser, because they virialise from a much denser
universe, due to expansion. The volumic density is going as
(1 + z)3, and the dynamical time-scale inside these haloes
is going as
 dyn ~ (1 +
z)-3/2. Therefore,
in addition to the larger fraction of mergers at z = 2,
the efficiency for a given merger to form stars is even higher.
The feedback mechanism, related to the life-time of OB stars,
has no reason to vary with redshift, and the time-scale to accrete
gas is shorter at high z.
dyn ~ (1 +
z)-3/2. Therefore,
in addition to the larger fraction of mergers at z = 2,
the efficiency for a given merger to form stars is even higher.
The feedback mechanism, related to the life-time of OB stars,
has no reason to vary with redshift, and the time-scale to accrete
gas is shorter at high z.
Also, it is easy to predict, since galaxies accumulate mass in
their bulge through secular evolution and galaxy interaction/merger,
that galaxies in the past were more unstable, having a smaller
bulge-to-disk ratio. Bar instability is then more violent,
with more gas accretion, and bars are destroyed also more
quickly. The fact that bars are transient might explain the
observed lower bar frequency, although the present observations
are still preliminary.
5.2. Relation between starburst and AGN
Starbursts and AGN compete for gas fuel. They relie on the
same dynamical mechanisms to be feeded and active.
The main consequence of radial gas flow due to bars and
gravity torques is not only a nuclear starburst and an AGN, but
also the bulge growth, and a massive black hole growth.
However, the amount of gas required to grow the BH over Gyrs is small,
ensuring that both can occur simultaneously, which is reflected in the
observed correlation between the final masses:
MBH = 0.1-0.2% Mbulge
(Magorrian et al 1998,
Ferrarese & Merritt
2000).
The relation between starbursts and AGN is not only circumstancial,
but there are effective regulation from one to the other and
reciprocally. For instance, the central BH mass can modify
the central dynamics, so as to favor gas accretion, or instead
to destroy a bar, and stop accretion and star formation.
Nuclear starbursts produce outflows (such as M82, N253)
that regulate the BH grow, while the compact stellar clusters formed can
provide fuel to the BH through stellar mass loss (e.g.
Norman & Scoville
1988).
Although there is a massive black hole in almost every galaxy today,
most of them are quiescent. According to quasars counts and
luminosity as a function of redshift (e.g.
Boyle et al 1991),
QSOs were more numerous and more powerful in the past.
This means that those black holes that were active were more massive,
while at low redshift, only more modest black holes are entering
their activity cycle
(Haehnelt & Rees
1993).
We can deduce that the AGN-starburst connection at high
redshift was a little different than today: composite objects
were more dominated by their AGN, due to their greater
black hole mass.
Another point comes from their lower bulge mass: the inner
Lindblad resonance was less frequent, and in this case
the gas can be accreted all the way down to the nucleus,
since it is not stalled at ILR. Of course, the time-scale
of gas accretion is longer when there is no resonance, but this
might be compensated by the shorter dynamical time-scale.
It is then likely that a black hole was easier to feed at high z.
Besides, the accretion being easier, the regulating mechanism
was operating faster, then destroying the bar after a shorter
time-scale. All these phenomena have to be tackled
in details, to determine their actual effect on evolution.
6. CONCLUSIONS
The detailed processes leading to star formation at large scales
in a galaxy disk or in the nucleus are still not well known.
Many physical mechanisms can explain observations:
gravitational instabilities, cloud-cloud collisions,
density-wave and radial flows, propagating
star-formation, galaxy interactions...
Empirical laws like the "global" Schmidt law do not help
in disentangling the role of all these physical phenomena.
Moreover, a "local" Schmidt law is still an unconfirmed
paradigm, since there is no tight correlation between local gas density
and SFR density.
The main factor towards giant starbursts is the quick flow
of gas in a concentrated region in a short enough time-scale (< 10 Myr),
to beat the stellar feedback processes.
This can only be provided by gravity torques in gaseous disks
(due for instance to galaxy interactions, that trigger bars, etc...)
This mechanism might be preponderant only at late Hubble times,
when galaxies are massive, with stabilising bulges.
At earlier times (z > 1), galaxies are less evolved and less
concentrated; they are not stabilised against gravitational instabilities;
those can be violent, triggering spontaneous bursts, with a chaotic
appearance,
accounting for the irregular and knotty images observed at high redshift.
Starbursts and AGN are often observed in symbiosis in galaxies,
they are not only fed by the same mechanisms, but sometimes
regulate each other.
The observations at high redshift help to get insight in the
time evolution of both, leading to parallel growth of bulges
and supermassive black holes. Dark haloes forming earlier are denser,
explaining why supermassive black holes
forming earlier are more massive
(Haehnelt & Kauffmann
2000).
Evolutionary cosmological models (N-body simulations + semi-analytical
experiments) succeed to some extent to reproduce observations:
they use a local Schmidt law for star formation
and introduce schematically the stellar feedback, by yielding
energy at each star formation to increase the bulk motion of the gas.
Simulations retrieve rather well the
slope of the Tully-Fischer relation, which appears to be
not very sensitive to SF prescriptions (e.g.
Steinmetz & Navarro
2000).
But there is a big problem to retrieve the zero point:
at a given rotational velocity, model galaxies are 2 magnitude dimmer
than observed galaxies. The problem is now well
identified, the dark matter is too much concentrated in the models,
and there is not enough baryons in the central regions of a galaxy disk.
This has also been remarked in fitting rotation
curves and in particular
of dwarf irregulars, that are dominated by dark matter.
This is independent of cosmological parameters (CDM, or
 CDM),
although the efficiency to transform baryons into stars is much higher
in CDM (~ 100%) than in
CDM),
although the efficiency to transform baryons into stars is much higher
in CDM (~ 100%) than in
 CDM (~ 40%)
(Navarro & Steinmetz
2000).
CDM (~ 40%)
(Navarro & Steinmetz
2000).
I am very grateful to Johan Knappen and collaborators for
the organisation of such a pleasant and fruitful conference, to their
sponsors and the CNRS for their financial help.
REFERENCES
Alonso-Herrero A., Engelbracht C.W., Rieke M.J.,
Rieke G.H., Quillen A.C.:
2001, ApJ 546, 952
Arsenault, R.:
1989, A&A 217, 66
Beck S., Turner J., Kovo O.:
2000, AJ 120, 244
Bekki K.:
1999, ApJ 510, L15
Benedict, F. G., Smith, B. J., Kenney, J. D. P.:
1996, AJ 111, 1861
Bottema, R.:
1993, A&A 275, 16
Boyle B.J., Jones L.R., Shanks T. et al.: 1991, in
"The Space Density of Quasars", ASP Vol 21, p. 191
Bureau, M., Freeman, K. C., Pfitzner, D. W., Meurer,
G. R.:
1999, AJ 118, 2158
Buta R., Treuthardt P., Byrd G., Crocker D.:
2000, AJ 120, 1289
Combes, F., Gerin, M., Nakai, N., Kawabe, R., Shaw,
M. A.:
1992, A&A 259, L27
Combes F.: 2000, in
"Molecular Hydrogen in Space",
eds. F. Combes & G. Pineau des Forêts, Cambridge Univ. Press,
p. 275
Coziol, R., Considère, S., Davoust, E., Contini, T.:
2000, A&A 356, 102
de Grijs R., O'Connell R., Gallagher J.:
2001, AJ 121, 768
Duc, P.-A., Brinks, E., Springel, V., Pichardo, B.,
Weilbacher, P., Mirabel, I. F.:
2000, AJ 120, 1238
Elmegreen B., Kaufman M., Thomasson M.:
1993, ApJ 412, 90
Emsellem E., Greusard, D., Combes F., Friedli D.,
Leon S., Pécontal E., Wozniak H.:
2001, A&A 368, 52
Ferrarese L., Merritt D.:
2000, ApJ 539, L9
Haehnelt M.G., Kauffmann G:
2000, MNRAS 318, L35
Haehnelt M.G., Rees M.J.:
1993, MNRAS 263, 168
Hawarden, T. G., Mountain, C. M., Leggett S.K.,
Puxley, P. J.:
1986, MNRAS 221, P41
Heckman, T. M., Dahlem, M., Eales, S. A., Fabbiano,
G., Weaver, K.:
1996, ApJ 457, 616
Huber D., Pfenniger D.: 2001, A&A preprint
(astro-ph/0105501)
Hunt L.K., Malkan M.A.:
1999 ApJ 516, 660
Jog, C.:
1992, ApJ 390, 378
Jogee S. & Kenney J.D.P.: 2000, in
"Dynamics of Galaxies: from the Early Universe to the
Present", eds
F. Combes, G. Mamon, V. Charmandaris, ASP Conf, Vol. 197, p. 193
Kenney, J. D. P., Benedict, G. F., Friedli, D.:
1998, BAAS, 193, 53.03
Kennicutt, R. C., Roettiger, K. A., Keel, W. C.,
van der Hulst, J. M., Hummel, E.:
1987, AJ 93, 1011
Kennicutt R.C.:
1989, ApJ 344, 685
Kennicutt R.C.:
1998, ApJ 498, 541
Klessen R.:
1997, MNRAS 292, 11
Knapen, J. H., Shlosman, I., Peletier R.F.:
2000, ApJ 529, 93
Koo B-C, McKee C.F.:
1992, ApJ 388, 93 &
103
Lefevre O., Abraham, R., Lilly, S. J., et al.:
2000, MNRAS 311, 565
Lelièvre M., Roy J-R.:
2000, AJ 120, 1306
Lin D.N.C., Pringle J.E.:
1987, MNRAS 225, 607
MacKenty J.W., Maiz-Apellaniz J., Pickens C., Norman
C., Walborn N.:
2000, AJ 120, 3007
Magorrian, J., Tremaine, S., Richstone, D., et al.:
1998, AJ 115, 2285
Maoz D., Barth A., Ho L.C., Sternberg A., Filipenko
A.:
2000, BAAS, 197, 78.02
Mihos J. C., Hernquist L.:
1994, ApJ 437, 611
Mihos, J.C., Hernquist, L.:
1996, ApJ, 464, 641
Navarro J., Steinmetz M.:
2000, ApJ 538, 477
Norman C., Scoville N.Z.:
1988, ApJ 332, 124
Peletier, R. F., Knapen, J. H., Shlosman, I., et
al.:
1999, ApJS 125, 363
Pompea S., Rieke G.:
1990, ApJ 356, 416
Puxley, P. J., Hawarden, T. G., Mountain, C. M.:
1988, MNRAS 231, 465
Quirk W.J.:
1972, ApJ 176, L9
Roberts M., Haynes M.:
1994, ARAA 32, 115
Rubio M., Lequeux J., Boulanger F.:
1993, A&A 271, 9
Rudnick G., Rix H-W., Kennicutt R.:
2000, ApJ 538, 569
Sakamoto, K., Okumura, S. K., Ishizuki, S.,
Scoville, N. Z.:
1999, ApJ 525, 691
Sakamoto, K., Baker, A.J., Scoville, N. Z.:
2000, ApJ 533, 149
Sanders D., Mirabel F.:
1996, ARAA 34, 749
Schinnerer E., Eckart A., Boller T.:
2000, ApJ 545, 205
Schmidt, M.:
1959, ApJ 129, 243
Schweizer F.: 2001, in
"Extragalactic Star Clusters", eds. E. Grebel,
D. Geisler, D. Minniti, IAU 207
(astro-ph/0106345)
Scoville N.Z.: 2000, in
"Dynamics of Galaxies: from the Early
Universe to the Present", eds F. Combes, G. Mamon, V. Charmandaris,
ASP Conf, Vol. 197, p. 301
Semelin B., Combes F.:
2000, A&A 360, 1096
Shioya Y., Taniguchi Y., Trentham N.:
2001, MNRAS 321, 11
Shlosman, I., Peletier, R. F., Knapen, J. H. :
2000, ApJ 535, L83
Silk J.:
1997, ApJ 481, 703
Steinmetz M. & Navarro J.: 2000, in
"Dynamics of Galaxies: from the Early
Universe to the Present", eds F. Combes, G. Mamon, V. Charmandaris,
ASP Conf, Vol. 197, p. 165
Surace, J. A., Sanders, D. B., Vacca, W, D.,
Veilleux, S., Mazzarella, J. M.:
1998, ApJ 492, 116
Tan J.:
2000, ApJ 536, 173
Taniguchi Y., Wada K.:
1996, ApJ 469, 581
Taniguchi Y., Ohyama Y.:
1998, ApJ 509, L89
Taniguchi Y., Trentham N., Shioya Y.:
1998, ApJ 504, L79
Taylor C.L., Kobulnicky H.A., Skillman E.D.:
1998, AJ 116, 2746
Telles E.: 2001, in
"Extragalactic Star Clusters", eds. E. Grebel,
D. Geisler, D. Minniti, IAU 207
(astro-ph/0106341)
Thompson R.:
2000, BAAS, 197, 117.03
van den Bergh S., Cohen J., Crabbe C.: 2001, ApJ,
preprint
(astro-ph/0104458)
Wada K., Norman C.:
1999, ApJ 516, L13
Wada K., Norman C.:
2001, ApJ 547, 172
Walter F., Taylor C., Hüttemeister S., Scoville
N., McIntyre V.:
2001, AJ 121, 727
Wyse R., Silk J.:
1989, ApJ 339, 700
Young J.S., Kenney, J. D., Tacconi, L., Claussen,
M. J., Huang, Y.-L., Tacconi-Garman, L., Xie, S., Schloerb, F. P.:
1986, ApJ 311, L17
Young J.S.:
1999, ApJ 514, L87
 OBSERVATIONS : WHERE ARE STARBURSTS LOCATED ?
OBSERVATIONS : WHERE ARE STARBURSTS LOCATED ?
 DYNAMICAL MECHANISMS
DYNAMICAL MECHANISMS
 Global statistical studies
Global statistical studies
 Parameters governing the SFR
Parameters governing the SFR
 Why are Q and
Why are Q and
 c
actually not
very useful to predict star formation trigger and starburst activity?
c
actually not
very useful to predict star formation trigger and starburst activity?
 Influence of bars
Influence of bars
 LARGE GAS COMPLEXES AND STELLAR CLUSTERS
LARGE GAS COMPLEXES AND STELLAR CLUSTERS
 FEEDBACK, REGULATION, PROPAGATION
FEEDBACK, REGULATION, PROPAGATION
 STARBURSTS AS A FUNCTION OF REDSHIFT
STARBURSTS AS A FUNCTION OF REDSHIFT
 More efficient star formation at high z
More efficient star formation at high z
 Relation between starburst and AGN
Relation between starburst and AGN
 CONCLUSIONS
CONCLUSIONS
 REFERENCES
REFERENCES

 /yr,
an estimation from NICMOS images in the Hubble Deep Field
conclude that both processus appear similar in importance
(
/yr,
an estimation from NICMOS images in the Hubble Deep Field
conclude that both processus appear similar in importance
( flux
for normal galaxies, to the Far Infrared luminosity L(FIR) for
starbursts, which are highly obscured
(
flux
for normal galaxies, to the Far Infrared luminosity L(FIR) for
starbursts, which are highly obscured
(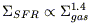
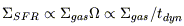
 is the angular
frequency in the galaxy, which is
inversely proportional to the dynamical time-scale tdyn.
is the angular
frequency in the galaxy, which is
inversely proportional to the dynamical time-scale tdyn.
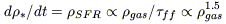
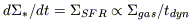

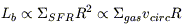

 dyn) ratio. Normal
galaxies are the
triangles, while starburst galaxies are the squares.
dyn) ratio. Normal
galaxies are the
triangles, while starburst galaxies are the squares.
 2,
that could imply a local Schmidt law. It is possible to account for
observations of SFR and SFE, by considering only collisions
(
2,
that could imply a local Schmidt law. It is possible to account for
observations of SFR and SFE, by considering only collisions
(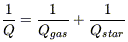
 in the stability.
When there is a large surface density of gas, the Qgas term
dominates, and it is justified to compute Q and
in the stability.
When there is a large surface density of gas, the Qgas term
dominates, and it is justified to compute Q and
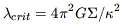
 2
2
 , and
, and
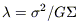
 G
G
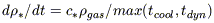
 CDM),
although the efficiency to transform baryons into stars is much higher
in CDM (~ 100%) than in
CDM),
although the efficiency to transform baryons into stars is much higher
in CDM (~ 100%) than in