


Dust is one of the most important components of the ISM, including roughly half of heavy elements synthesized by stars. The presence of dust is relevant in many astrophysical environments and has a crucial role in shaping the spectra of many cosmic bodies. However, its existence has been inferred from very indirect evidences up untill recently. The first evidence came from the discovery of a tenuous screen of small particles around the Earth producing the zodiacal light. Other evidences came from observations of dust trails of comets, circumstellar dust envelopes around evolved stars, diffuse dust in the MW producing the interstellar extinction, the discovery of IR emission by galaxies and ultra-luminous IR galaxies in the IRAS era, circumnuclear dust in AGNs (essential ingredient of the unified model for AGNs), the cosmological IR background (COBE, 1996-1998), and eventually the discovery of sites of extremely active star formation at high redshifts (SCUBA and ISO, 1998-2000).
Accounting for the effects of dust is essential not only to
understand the erosion of optical light, but, even more importantly,
to evaluate the energy re-emitted by dust at longer wavelengths,
typically at
![]()
![]() 5 to 1000 µ.
This is crucial for estimating all basic properties of distant galaxies:
the Star Formation Rate (SFR) from various optical and IR
indicators,
the ages of stellar populations, which, based as they are on
optical colours, have to
distinguish the reddening of the spectrum due to aging from that due to
dust extinction,
and finally to constrain the stellar initial mass function (IMF).
5 to 1000 µ.
This is crucial for estimating all basic properties of distant galaxies:
the Star Formation Rate (SFR) from various optical and IR
indicators,
the ages of stellar populations, which, based as they are on
optical colours, have to
distinguish the reddening of the spectrum due to aging from that due to
dust extinction,
and finally to constrain the stellar initial mass function (IMF).
Rather than by stars, the available volume in a galaxy is occupied by the
ISM, which in local late-type
systems amounts to ![]() 10% of the baryonic mass. The ISM includes gas mixed
with tiny solid particles, the dust, with sizes ranging from a few
Å (the PAH molecules) up to
10% of the baryonic mass. The ISM includes gas mixed
with tiny solid particles, the dust, with sizes ranging from a few
Å (the PAH molecules) up to
![]() 10 µm. The mass in dust is typically 0.5 to
1% of the ISM mass.
10 µm. The mass in dust is typically 0.5 to
1% of the ISM mass.
The mechanisms of birth, growth and destruction of grains are very complex and poorly understood. It is believed that condensation nuclei for dust grains mostly form in dense regions of the ISM, which are better shielded from UV photons. Main dust production sites are hereby listed.
Envelopes of protostars: during the process leading to the birth of a star a solar nebula is produced, where silicate grains can be formed and then blown away by a Pre-Main Sequence wind (T Tauri phase).
Cold evolved stars: in the cold atmospheres of evolved giants,
dust grains can form
and drive a strong stellar wind, in particular graphite grains
from carbon stars and silicate grains in OH-IR stars. Stars with
M < 8M![]() are important dust producers; higher-M stars, like Wolf-Rayets
with high mass-loss rates, are too rare.
are important dust producers; higher-M stars, like Wolf-Rayets
with high mass-loss rates, are too rare.
Type-II supernovae are probably the most important contributors, as revealed by a variety of tests, like those provided by the IR excesses in the light-curve and the extinction of background stars in SN ejecta. Direct evidences of dust production came from the case-study of SN 1987a (CO and SiO molecules found in the ejecta), the dark spots observed in the synchrotron nebula of Crab, the IR mapping by ISO of Cas-A which resolved clumpy emission associated with the fast moving knots (Lagage et al. 1996).
Type-I supernovae have an uncertain role, with no evidence yet for dust formation (which would be otherwise relevant to solve the problem of the Fe depletion).
The general interstellar medium is also the site of a slow growth around pre-existent condensation nuclei (refractory cores); it is in this way that dirty icy grains are produced.
Grain survival is another, uncertain, chapter of the complex story of dust enrichment of the ISM. Grain destruction is not likely a problem in stellar winds, the grain should survive the injection into the ISM, while it is more a problem for SN ejecta (which have typical velocities in excess of 1000 Km/s).
Even after the ejection phase, the ISM is in any case a difficult environment for grain survival: grains can be destroyed there by evaporation, thermal sublimation in intense radiation fields, evaporation in grain-grain collisions, and by radiative SN shocks.
2.2.3. The evolution of the dust content in a galaxy
Modelling the complex balance between grain production and destruction
is also guided by
observations of isotopic anomalies in meteorites and of the elemental
depletion pattern.
A detailed account of most plausible intervening processes in the dust
life cycle can be found in
Dwek (1998).
The author also discusses evolution paths of the elemental abundances
in the gas and dust phases in a typical spiral galaxy, based on standard
assumptions for the infall of primordial gas and chemical evolution.
Type-II SN are found to be the main producers of silicate dust in a
galaxy, while carbon
dust is due to lower mass (2-5 M![]() ) stars. The different lifetimes of
the two imply
likely anomalous abundance ratios between the various dust grain types
during the course of
galaxy evolution, naturally evolving from an excess of silicate to an
excess of carbon grains with galactic time.
) stars. The different lifetimes of
the two imply
likely anomalous abundance ratios between the various dust grain types
during the course of
galaxy evolution, naturally evolving from an excess of silicate to an
excess of carbon grains with galactic time.
Altogether, the dust mass is found to be linearly proportional to the gas metallicity and equal to 40% of the total mass in heavy elements in a present-day galaxy. Although the details can depend to some extent on the evolution of the SFR with time (e.g. in the case of elliptical galaxies this evolution could have been more rapid, see Mazzei, De Zotti & Xu 1994), these general results are not believed to be much affected.
2.3. Interactions between dust and radiation
Dust particles interact with photons emitted by astrophysical sources by
absorbing,
scattering, and polarizing the light (the combined effect of absorption and
scattering takes the name of extinction). They also emit photons at
wavelengths typically much greater than those of the absorbed photons.
The total intensity radiation field
I![]() (
(![]() , t) (defined as usual by
dE
, t) (defined as usual by
dE ![]() I
I![]() d
d![]() d
d![]() dAdt, dE being the differential amount of
radiant energy) is related to the field sources by the transfer
equation:
dAdt, dE being the differential amount of
radiant energy) is related to the field sources by the transfer
equation:
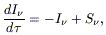
| (2.1) |
where
d![]()
![]()
![]() ds is the differential optical depth
corresponding to a spatial path ds,
S
ds is the differential optical depth
corresponding to a spatial path ds,
S![]()
![]() j
j![]() /
/![]() is the source function,
is the source function,
![]() and j
and j![]() being the extinction (true
absorption
+ scattering) and emission (true emission + scattering) coefficients.
A medium is said optically thin or thick if
being the extinction (true
absorption
+ scattering) and emission (true emission + scattering) coefficients.
A medium is said optically thin or thick if
![]() along a typical path trough the medium is
<< 1 or >> 1.
Absorption includes those processes in which the energy of photons
is turned into other forms (may be internal energy of matter or fields),
true emission is the opposite processe, whilst in scattering the energy
of photons is simply deviated into other directions.
Dust scattering is usually elastic. A formal solution to eq.(1) [e.g.
Rybicki & Lightman
1979] is given by:
along a typical path trough the medium is
<< 1 or >> 1.
Absorption includes those processes in which the energy of photons
is turned into other forms (may be internal energy of matter or fields),
true emission is the opposite processe, whilst in scattering the energy
of photons is simply deviated into other directions.
Dust scattering is usually elastic. A formal solution to eq.(1) [e.g.
Rybicki & Lightman
1979] is given by:
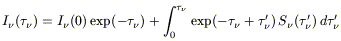
| (2.2) |
If each dust grain has a ![]() -dependent effective cross section
-dependent effective cross section
![]() and spatial density n, then
and spatial density n, then
![]() = n
= n ![]() or
or
![]() = N
= N ![]() , where N is
the column density. For dust grains it is common to write
, where N is
the column density. For dust grains it is common to write
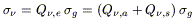
|
where ![]() is the geometrical cross section (
is the geometrical cross section (![]() a2 for spheres)
and Q
a2 for spheres)
and Q![]() , e is the extinction efficiency (true
absorption + scattering).
At short-
, e is the extinction efficiency (true
absorption + scattering).
At short-![]() (UV), diffraction effects in the photon-grain
interaction become
negligible, and the effective cross-section coincides with the geometric
one,
Q
(UV), diffraction effects in the photon-grain
interaction become
negligible, and the effective cross-section coincides with the geometric
one,
Q![]() , e
, e ![]() 1. Altogether:
1. Altogether:
![]() = Q
= Q![]() , e
, e![]() n.
n.
The albedo
a![]() = Q
= Q![]() , s/Q
, s/Q![]() , e is the fraction
of extinguished light being scattered by the grain rather than absorbed.
, e is the fraction
of extinguished light being scattered by the grain rather than absorbed.
The emission coefficient j![]() includes a true emission
j
includes a true emission
j![]() , e and an elastic scattering
component, j
, e and an elastic scattering
component, j![]() , s, given by:
, s, given by:
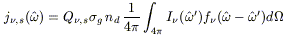
|
where f![]() is the phase function, depending
on the incidence-scattering angle.
is the phase function, depending
on the incidence-scattering angle.
The true emission of dust grains is thermal.
From Kirchoff's law [j![]() =
= ![]() B
B![]() (T)]:
(T)]:
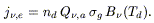
| (2.3) |
It is clear that both terms of the emission coefficient depend on
the radiation field I![]() . In particular j
. In particular j![]() , e depends on it trough the dust grain
temperature T: grain heating is almost always dominated by the
radiation field.
Thus a primary task is to compute T. Two situations apply.
, e depends on it trough the dust grain
temperature T: grain heating is almost always dominated by the
radiation field.
Thus a primary task is to compute T. Two situations apply.
(a) Grains sufficiently large and massive don't cool in the time interval between absorption of two photons: they are in thermal equilibrium with the radiation field. Their temperature can be determined by solving for T an energy conservation equation absorbed energy = emitted energy:
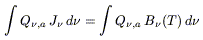
| (2.4) |
where
J![]() = 1/4
= 1/4![]()
![]() I(
I(![]() ,
,![]() )d
)d![]() is the angle-averaged I
is the angle-averaged I![]() .
.
(b) Small grains fluctuate in temperature at any acquired photon. They never reach thermodynamic equilibrium (the cooling time is shorter than that between two photons arrivals). A probability distribution P(T)dT to find a grain between T and T + dT can then be computed based on a statistical approach (Puget et al. 1985; Guhathakurta & Draine 1989, Siebenmorgen & Kruegel 1992). Basic ingredients for this computation are:
- the specific heat C(T, a) per C-atom of PAH's of size a and the number Nc of C atoms in the grain;
- the maximum T a PAH can attain after absorption of a photon h![]() , and
given by the relation:
, and
given by the relation:
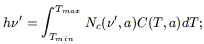
|
- the cooling rate of a PAH after being heated to Tmax is
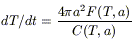
|
where
F(T, a) = ![]() Qabs(
Qabs(![]() , a)
, a)![]() B(
B(![]() , T)d
, T)d![]() is the power radiated per unit grain surface.
The total IR spectrum radiated during the cooling down is:
is the power radiated per unit grain surface.
The total IR spectrum radiated during the cooling down is:
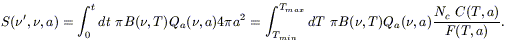
|
In any case, dust grains are destroyed by radiation-induced temperatures
above ![]() 1000 ÷ 2000 K (depending mainly on
composition). This is
the reason why their emission is relevant only longwards a few
µm.
1000 ÷ 2000 K (depending mainly on
composition). This is
the reason why their emission is relevant only longwards a few
µm.
For mixtures of different species of particles the equations must be summed over all the species. For spherical grains of different compositions and sizes a and density ni(a):
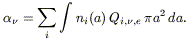
|
The interaction of a dusty medium with the radiation field then requires
the knowledge of the quantities Q![]() , a, Q
, a, Q![]() , s and f
, s and f![]() .
The Mie (1908)
theory provides analytic solutions for homogeneous spheres and infinite
cilinders. Otherwise, for irregularly shaped and inhomogeneous grains good
approximations can be obtained by simple generalizations of the exact
solutions for spheres and cylinders (e.g.
Hoyle & Wickramasinghe
1991;
Bohren and Huffman 1983).
.
The Mie (1908)
theory provides analytic solutions for homogeneous spheres and infinite
cilinders. Otherwise, for irregularly shaped and inhomogeneous grains good
approximations can be obtained by simple generalizations of the exact
solutions for spheres and cylinders (e.g.
Hoyle & Wickramasinghe
1991;
Bohren and Huffman 1983).
As a source of scattering (like the e-), another important effect of dust is to induce polarization in the emitted light. Two ways for dust to produce this are through (a) light transmission in a dusty medium including oriented bipolar components; or (b) dust reflection (e.g. in AGNs). Should we be interested in modelling these effects of dust on polarization, then solutions of the transfer equation (2.1) for all four Stokes parameters would be required.
2.4. Alternative heating mechanisms for dust
Two other heating mechanisms for dust grains can operate (Xu 1997).
(a) Collisional heating for dust mixed with thermal gases. In the HI component of the solar neighbourhood the ratio of collisional heating Gcoll to radiative heating Grad turns out to be
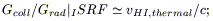
|
i.e. the collisional is 5 orders of magnitude less than radiative heating! Only in very hot plasmas (IC plasmas at T > 107) the two can get comparable.
(b) Chemical heating, a process occurring typically in the cold gas component of the ISM, e.g. when an H2 molecule is formed on the surface of a grain from the combination of 2 H atoms:
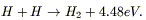
|
Most of this chemical energy is absorbed by the grain (the rest is taken by the molecule). The released energy turns out comparable with the collisional one (hence negligible).
2.5. The interstellar extinction curve
Before IRAS, the properties of interstellar dust were mainly inferred
from the dimming of optical light of stars inside the Galaxy.
If we observe the light from a source through a dust screen, dust
emission is negligible in the optical (dust emits significantly only in
the IR), offline scattering is unimportant, and the formal solution
(eq. 2.1) simplifies to
I![]() = I
= I![]() (0)e-
(0)e- ![]() . Given a source with
unextinguished flux
m
. Given a source with
unextinguished flux
m![]() (0), the extinction in magnitudes is:
(0), the extinction in magnitudes is:
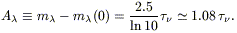
|
The knowledge of the intrinsic colors for a source population allows to
determine the wavelength dependence of the extinction curve.
The mean extinction curve along most line-of-sights in the Milky Way has
been studied by many authors (see references in
Hoyle & Wickramasinghe
1991;
and see Figure 1).
Its main properties are:
(a) a growth in the optical-near UV, more than linear with
frequency,
![]()
![]()
![]()
![]()
![]() (0.6 - 5 µm);
(b) a bump around 2175 Å;
(c) a steeper rise in the far-UV;
(d) two features in the mid-IR at 9.7 and 18µm.
(0.6 - 5 µm);
(b) a bump around 2175 Å;
(c) a steeper rise in the far-UV;
(d) two features in the mid-IR at 9.7 and 18µm.
The extinction curve is not universal: in the Milky Way it depends on the line of sight. Data on other stellar systems (LMC and SMC for example) suggest a variable behaviour, in particular in UV.
More recently it has been possible to evaluate indirectly the extinction curve is distant galaxies, by means of accurate photometric observations in narrow-band filters. Gordon et al. (1997) (see also Calzetti 1997) analyze colour-colour plots for 30 starburst galaxies, inferring starburst ages and extinction properties. The 2175 Å bump is absent and the rise in the far-UV slower than observed for the Milky Way. The authors suggest that the starburst has modified the grain distribution, in particular suppressing the 2175Å feature observed in the MW. Alternatively, Granato et al. (2000) reproduce the observed extinction law in starbursts as a purely geometrical effect, by using the same dust grain mixture than for the MW and accounting for differential extinction for young and old stars (see Sect. 4 below).
2.6. Models of the interstellar dust
The extinction curve, whose main features are reported in
Fig. 1,
can be explained by a mixture of grains with different sizes and
compositions. The curve in the optical is reproduced by grains with
a ![]() 0.1µm,
while the fast growth of the extinction curve in UV requires smaller
particles with
a
0.1µm,
while the fast growth of the extinction curve in UV requires smaller
particles with
a ![]() 0.01µm. Silicate grains explain the 9.7
µm
and 18 µm emission features, whose large widths
suggest the presence of many impurities (dirty or
astronomical silicates).
0.01µm. Silicate grains explain the 9.7
µm
and 18 µm emission features, whose large widths
suggest the presence of many impurities (dirty or
astronomical silicates).
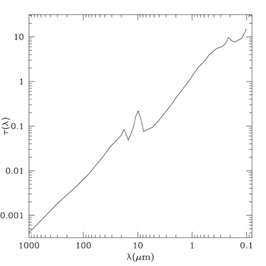
|
Figure 1. The galactic extinction curve, in optical depth per unit value of E(B - V). The two silicate features at 10 and 18 µm and that of carbonaceous grains at 2175 Å can be recognised. |
On the contrary, silicates cannot explain the optical extinction, because of their excessive albedo. Here carbonaceous grains (graphite or amorphous carbon) are proposed as main absorbers, their resonance at 2175 Å nicely fitting the observed UV bump. The non-linear growth in the FUV is probably due to very small grains and PAH molecules (required also to explain the interstellar IR emission bands, e.g. Puget & Leger 1989).
Unfortunately, the extinction curve does not constrain enough the properties of interstellar dust. For this reason, a variety of models, all with the above basic ingredients, have been proposed to reproduce it.
Draine and Lee (1984)
adopt a power law size distribution of silicate and graphite grains
dn/da ![]() nHa-3.5 for 0.005
µm < a < 0.25µm.
A quite more complex model by
Siebenmorgen & Krugel
(1992)
includes five classes of
grains (amorphous carbon, silicates, very small grains, small PAH
and clusters PAH), providing an impressive fit to the extinction
curve. The one by
Rowan-Robinson (1992)
with a discrete set of nine kinds of grain (amorphous carbon size
a = 30µm and
a = 0.1µm; graphites with a = 0.03,
0.01, 0.002 and 0.0005 µm; amorphous silicate
a = 0.1µm and silicates with a = 0.03
and 0.01 µm)
explains also the FIR emission from circumstellar envelopes.
The population of very big grains is assumed here to explain the
sub-mm emission of carbon stars.
nHa-3.5 for 0.005
µm < a < 0.25µm.
A quite more complex model by
Siebenmorgen & Krugel
(1992)
includes five classes of
grains (amorphous carbon, silicates, very small grains, small PAH
and clusters PAH), providing an impressive fit to the extinction
curve. The one by
Rowan-Robinson (1992)
with a discrete set of nine kinds of grain (amorphous carbon size
a = 30µm and
a = 0.1µm; graphites with a = 0.03,
0.01, 0.002 and 0.0005 µm; amorphous silicate
a = 0.1µm and silicates with a = 0.03
and 0.01 µm)
explains also the FIR emission from circumstellar envelopes.
The population of very big grains is assumed here to explain the
sub-mm emission of carbon stars.
The most relevant recent improvement with respect to the classical models by Drain & Lee is the addition to the grain mixture of very small particles and macro-molecules reaching temperatures higher than equilibrium because of their small size, as described above. Two regions of the extinction curve are particularly sensitive to the presence of these small particles: the mid-IR spectrum (including the emission bands at 3.28, 6.2, 7.7, 8.6 and 11.3 µm, and appreciable continuum), and the fast far-UV rise.
The mid-IR emission bands, in particular, are most commonly interpreted as due to a family of very stable planar molecules, the PAH's (polyciclyc aromatic hydrocarbons), whose vibrational spectra closely resemble, according to laboratory tests, those of emission bands. PAH emission features originate mainly in the so-called photo-dissociation regions, i.e. in the interfaces between molecular clouds and the HII regions, where the cloud surfaces are illuminated by the high energy field of the young stars. There are evidences that in denser environments and stronger UV field intensities the PAHs (and the associated mid-IR bands) could be depleted. In the circum-nuclear dusty regions around AGNs PAH emission is not observed.
PAH emission features have been observed by ISO to display Lorentian profiles, whose broad overlapping wings may mimic a kind of continuum (Boulanger et al. 1998). This may possibly explain the observed underlying mid-IR continuum in many astrophysical objects.