


Knowing, or guessing, the optical properties of dust, one can predict the spectra of dusty systems. From a computational point of view, we have to distinguish two cases.
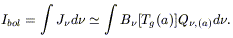
| (3.5) |
Since ![]() B
B![]() [Tg(a)]d
[Tg(a)]d![]() = aTg4 and because of the
additional dependence implied by Q
= aTg4 and because of the
additional dependence implied by Q![]() ,(a)
,(a) ![]()
![]()
![]() T1.5 - 2, the grain
equilibrium temperature Tg is found to depend very
weakly on the intensity of the local radiation field:
T1.5 - 2, the grain
equilibrium temperature Tg is found to depend very
weakly on the intensity of the local radiation field:
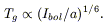
| (3.6) |
This implies that dust emission spectra in a variety of galactic
environments
(from quiescent to actively starbursting galaxies and AGNs)
are quite stable and robust, with peak emission mostly confined to the
wavelength interval ![]()
![]() 100 to 30
100 to 30 ![]() m.
Longward of
m.
Longward of ![]() and after eq. (2.3), dust spectra converge
according to the RJ law as
and after eq. (2.3), dust spectra converge
according to the RJ law as
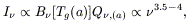
|
in agreement with mm observations of local IRAS galaxies by Andreani & Franceschini (1996) and Chini et al. (1995).
3.1. Radiative transfer in thick dusty media
In most practical cases, the radiative transfer equation can be solved only with numerical techniques. We mention in this Section a couple of such approaches quite often used.
3.1.1. Numerical solutions based on iterative schemes
A first class of solutions adopt an iterative numerical scheme based on applications of the formal solution of the transfer equation (eq.[2]). This was originally developed for interpreting AGN spectra (Granato & Danese 1994; Pier & Krolick 1992; Granato, Danese & Franceschini 1997), but is useful to treat more generally radiative transfer in thick media. Although the source function can be any kind in principle, we discuss here an application by Granato & Danese for a central point-source and for a planar and azimuthal symmetry of the dust distribution within a minimum rm and maximum rM radii. A condition is set on rm because of dust sublimation: it cannot be lower than rm = L460.5 T1500-2.8 (pc) to avoid exceeding an equilibrium grain temperature of Tgr = 1500 for graphite and Ts = 1000 for silicates.
The two fields to solve for are the radiation field intensity
I![]() (r,
(r,![]() ,
,![]() ,
,![]() )
and the grain temperature distribution
T(r,
)
and the grain temperature distribution
T(r,![]() ).
The solution is found by representing the field intensity as the
contribution of two terms
).
The solution is found by representing the field intensity as the
contribution of two terms
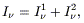
| (3.7) |
the first term being the radiation field emitted by the central source and estinguished by the dust, with trivial solution from eq. (2.1):
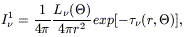
| (3.8) |
L![]() (
(![]() ) becoming dependent on direction because of differential
extinction,
) becoming dependent on direction because of differential
extinction, ![]() being the optical depth to the point (r,
being the optical depth to the point (r, ![]() ,
, ![]() ).
The second term originates from thermal emission by dust, and may be
expressed at the
zero-th order as the formal solution (eq. 2.2) of the transfer equation:
).
The second term originates from thermal emission by dust, and may be
expressed at the
zero-th order as the formal solution (eq. 2.2) of the transfer equation:
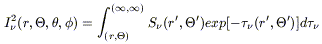
| (3.9) |
The quantity S![]() is the source function
j
is the source function
j![]() /
/![]() which,
if the scattering is isotropic, can be expressed as a weigthed average
of the scattering and absorption
(Rybicki and Lightman 1979)
summed over all grain species:
which,
if the scattering is isotropic, can be expressed as a weigthed average
of the scattering and absorption
(Rybicki and Lightman 1979)
summed over all grain species:
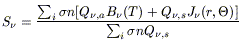
| (3.10) |
The function J![]() is the direction-averaged radiation
field intensity
is the direction-averaged radiation
field intensity
![]() I
I![]() d
d![]() : this integral obviously includes both contributions
to the total intensity in eq. (3.7).
Finally, assuming radiative equilibrium for the dust grains, the grain
temperature
distribution is found from eq. (2.4). The following iterative scheme is
used to obtain a solution for I
: this integral obviously includes both contributions
to the total intensity in eq. (3.7).
Finally, assuming radiative equilibrium for the dust grains, the grain
temperature
distribution is found from eq. (2.4). The following iterative scheme is
used to obtain a solution for I![]() :
:
(1) the zero-th order approximation for I![]() 1 in eq. (3.7) is obtained from
eq. (3.8) given L
1 in eq. (3.7) is obtained from
eq. (3.8) given L![]() and the adopted dust distribution;
and the adopted dust distribution;
(2) then a zero-th value for the T-field is found from eq. (2.4);
(3) the source function S![]() is then computed from eq. (3.10)
including the contribution from thermal dust emission;
is then computed from eq. (3.10)
including the contribution from thermal dust emission;
(4) after eq. (3.9) the second term I![]() 2 of the radiation field is
computed
and the total field intensity in eq. (3.7) is updated;
2 of the radiation field is
computed
and the total field intensity in eq. (3.7) is updated;
(5) convergence is achieved when e.g. dT from one step to the other is less than a small fixed amount. Suitable scaling rules are usually adopted to accelerate the convergence.
The advantage of brute-force solutions like a Monte Carlo simulation is that it is better suited to treat complex situations for the geometries of the source function and of the spatial distribution of the absorber. Also velocity fields can be naturally considered in the code to map the kinematical structure of the emission lines (e.g. Jimenez et al. 2000).
The usual approach is to assume a given geometrical distribution for the absorber, possibly including a velocity field, and to generate inside (or outside) it photons according to a given source function (plus a background photon distribution). All these fields are usually discretized into appropriate spatial grids. Each photons are then followed through the distribution of the absorber, their interaction being ruled by the optical depth, albedo and scattering phase functions at that point. The simplest geometrical distributions adopted are (e.g. Disney et al. 1989; Gordon et al. 1997): the mixed, in which the source and absorber are homogeneously distributed; the shell, where the source and absorber are separated, typically the former inside and the latter outside acting as a screen. However, much more complex situations can be described this way, up to fully 3D distributions without any symmetries (Jimenez et al. 2000).