


To understand the selection effects in 21 cm HI astronomy, we will examine the observing procedures in detail. The spectral survey has some basic differences from optical surveys and some unique problems. For the most part, I will refer to single-dish observations in which a single spectrum in a single direction is observed at one time. This is changing somewhat as the field moves in the direction of synthesis array systems and multiple receivers, but the individual radio spectrum is still the basis of most 21 cm detections.
Radio observations are usually made with what is known as the "total power" or "on-off" method. In this method, illustrated in Figure 8, the position of a suspected HI source (the on position) is observed along with an identical observation in an empty (off) region. The total power detected at each frequency in the off scan is subtracted from the on scan to remove background emission, persistent interference, and instrumental response characteristics. The result, as shown in the figure, is a spectrum relatively free of features in which the HI signal of the galaxy stands out.
The sample spectrum in Figure 8 shows a few of the features frequently encountered. The galaxy appears to have a few mJy of radio continuum emission, which shows up as a broadband difference between the on and off spectra. In addition, there is a small amount of curvature in the baseline regions of the difference spectrum. This might be real, but it is more likely due to slight frequency response differences in the receivers between the two times and for the two total powers of the on and off positions. Baselines are commonly removed by subtracting a polynomial fit to regions outside of the frequency range where line emission is believed to be present. It is important to note that this baselining procedure can hide wide HI features or generate false signals when high-order polynomials are needed to match the spectrum's shape.
There are also small residual features where man-made interference and local Galactic emission have been imperfectly subtracted. Galactic emission makes searches for sources with redshifts smaller than a few hundred km s-1 difficult. Interference is not always easily identified, and it can enter at a variety of frequencies. As illustrated by the frequency scales at the top of Figure 8, the heterodyning procedures used in 21 cm observations allow interference to enter at several different frequencies besides the 21 cm range. It may be introduced in one or more intermediate frequency ranges (where most of the amplification is done) or in the baseband frequency range (where the autocorrelation spectrometer operates). This interference usually appears as a nearly self-subtracted feature swinging positive and negative within a narrow span of frequencies. This identifying sign-reversal reflects small changes in frequency between the times of the on and off scans or by a changing redshift Doppler correction in that time span.
Interference is sometimes less easily identified, as when it occurs only or mostly during the on scan. This can become very difficult to disentangle from real extragalactic emission. A 21 cm "nightmare" of interference is illustrated in Figure 9. This is one of the most confusing spectra I have encountered, but it illustrates how a real signal can be identified despite rampant interference. The spectrum shown is split up into the left and right circular polarizations that were simultaneously observed. Since HI emission is normally unpolarized, the polarizations are usually combined to improve the signal-to-noise. However, interfering sources are often highly polarized, so by studying the polarizations separately these sources can be identified. Since the system is relatively well-shielded at the intermediate frequencies, I suspect most of the interference entered at the sky frequency, even within the 21 cm "protected band" at frequencies higher than 1400 MHz.
There is also some broad interference that was probably introduced around 16 MHz in the baseband. This can be identified as baseband interference because two ranges of sky frequency were observed simultaneously (in order to span a wider range of redshifts). Since similar (though polarized) interference is seen at the same relative position in both of the right circularly polarized spectra, this signal is likely entering at a single baseband frequency. Given the frequency involved and the fact that a shielded door to the computer room was accidentally left open, it appears likely that this interference was generated within the observatory itself.
Even the galaxy detected in this spectrum is difficult to recognize because there is some interference overlapping it. However, it is the only signal with a consistent strength in both polarizations and without a parallel feature seen entering through the baseband in the other redshift range. This spectrum was so problematic that the observation was repeated (with the shielded door closed!), and the source was confirmed, but in principle the redundancy in the data allows one to identify sources despite widespread interference.
An implicit aspect of identifying these HI features in 21 cm spectra is the expected shape of the feature. In Figures 8 and 9 I've illustrated the two common classes of HI profiles, the so-called two-horn and one-horn profiles. Two-horned profiles are produced by rotating disks seen at an inclination larger than ~ 20°. The gas on opposite sides of the center is Doppler shifted to higher or lower frequencies than the systemic redshift of the galaxy, and combined with the flat rotation curves this results in strong emission at two frequencies. Single-horn profiles are produced by face-on disk galaxies, dwarfs, and irregulars, where random motions and/or the lack of a flat rotation curve generate a roughly Gaussian shape. See Skillman (chapter 8) for a more complete discussion.
In general, it is assumed that a
5- signal would be identified,
where
signal would be identified,
where  is based on the
line-width of the signal. For example, a
wide signal like that in Figure 8 has
uncorrelated noise
entering in each of the Nch = 45 channels over which
the signal is seen. Since each channel is
is based on the
line-width of the signal. For example, a
wide signal like that in Figure 8 has
uncorrelated noise
entering in each of the Nch = 45 channels over which
the signal is seen. Since each channel is
 v = 8
km s-1 wide, and has an
rms uncertainty of
v = 8
km s-1 wide, and has an
rms uncertainty of  ch
= 4 mJy, the total noise is:
ch
= 4 mJy, the total noise is:
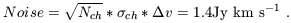
| (6) |
The signal is the sum of the fluxes detected in each channel. In this
case average signal strength is
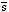 HI = 46 mJy above the
continuum + baseline, so that the total signal is:
HI = 46 mJy above the
continuum + baseline, so that the total signal is:
| (7) |
Thus a wide feature with the same mean flux density is in principle easier to detect than a narrow feature, although in objects with the same integrated signal the one that is narrower is easier to detect.
As with optical identifications, expectations about the shape of HI signals result in an additional selection effect that is difficult to quantify. Most observers will dismiss very narrow signals in a 21 cm spectrum if they are less than ~ 30 km s-1 wide, since such narrow lines are uncommon for galaxies but common for interference. On the other hand, wide profiles that do not have the expected steep sides may be assumed to be part of the baseline variations.
With these cautions in mind, we would like to survey the sky at 21 cm for HI sources in a way comparable to the great optical surveys. Given the integration times needed, and the point-by-point way in which 21 cm spectra are collected, observing the whole sky is impractical. Even a few square degrees require a significant amount of observing time, with little promise of any significant detections. As a result, large blind surveys have been made only rarely.
In some sense an enormous blind survey, consisting of all of the off scans ever collected, actually has been carried out already, but the data are not easily accessible. As discussed in the introduction to this chapter, a few objects have been discovered in off scans. However, the off scans tend to examine regions of the sky and redshifts that "shadow" the locations of cataloged galaxies, which introduces a potential bias into such a sample. Moreover, my impression is that the observers who have examined off scans for this purpose, myself included, have rarely devoted the sort of careful attention to possible weak signals in the off scan that they do to on scan positions where they expect to see a signal. After all, interference is so common that it hardly seems worth tracking down every small blip. Therefore the statistical results from these off-scan surveys are suspect.
A systematic blind survey has the advantage that interference can be monitored and persistent sources can be identified. Unlike a randomly placed off beam, a blind survey can map contiguous regions so that the survey is likely to get a "close hit" on a source as opposed to detecting it in the fringes of the beam. This sort of systematic mapping also allows for a much more efficient use of observing time, since the spectra can act as off scans for each other. By combining many scans into a single off, the noise introduced by the off scan can be almost entirely eliminated, resulting in an almost four-fold improvement over targeted on-off observations.
When observing a region of sky in a blind survey, the strategy is to maximize the effective search volume for the HI mass of the objects being sought. A fundamental choice that must be made in carrying out such a survey is illustrated in Figure 10: One can observe a large volume of space by either taking relatively few spectra of a distant region of space, or by making many more observations of a nearby volume of space.
It is not immediately obvious which is the more practical approach, although it can be shown that shallower surveys are generally more efficient. Consider a galaxy of a particular HI mass as illustrated in Figure 10. If that mass could be detected to twice the distance, we would expect to see 23 = 8 times as many of these galaxies because of the increase in volume. However, at twice the distance, the signal is only 1/4 as strong, so the integration time to detect this mass is 16 times larger. Therefore it would take twice as long to survey the same volume of space as it would if we made 8 separate observations in different directions.
Taking this idea to its logical extreme the conclusion is that, given a fixed amount of observing time, it is optimal to observe as many positions as possible with the shortest possible integration time per position. This needs to be moderated slightly to recognize that very short integrations may not be useful (there aren't many galaxies within 1 kpc of us!), and the Doppler redshifts of HI in the Milky Way prevent us from detecting galaxies at redshifts smaller than ~ 300 km s-1. (Actually, massive galaxies can often be identified at low redshifts because of their distinct two-horn profile shape, but this is a minor point in terms of available search volume.) In addition, telescopic observations may become inefficient if integrations become so short that more time is spent moving the telescope than integrating on-source. A further limitation is that nearby galaxies usually have large angular diameters, so only a fraction of a galaxy will be detected within the telescope beam, and the integration times no longer improve at small distances. The ideal appears to be to integrate just long enough to detect the lowest-mass galaxies we are interested in several times further away than the distance at which their angular size matches the telescope beam size.
Having selected a survey strategy with a particular detection limit, the telescope detects the more massive galaxies out to higher redshifts. The detectable volume for these galaxies is larger in proportion to the cube of their detectable distance limit (equation 5) or MHI3/2. The bandwidth of the spectrum can introduce an upper limit on the volume for massive galaxies, and, depending on the set-up employed, there could be a limit at small redshifts as well.
The effective volumes surveyed in a number of the largest studies are shown in Figure 11. The effective volume for each survey is calculated from the velocity range and resolution, rms noise, beam size, and total number of points observed. The surveys by Krumm & Brosch (1984), Henning (1992), Shostak (1977), and Fisher & Tully (1981) were made at the Green Bank 300 ft telescope. The survey by Weinberg et al. (1991) was carried out at the VLA. The "Arecibo Slice" survey is a recent survey described later in this chapter.
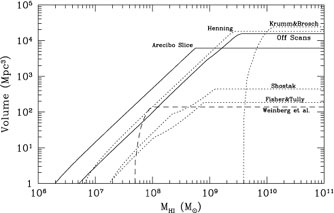
|
Figure 11. Volumes of space searched as a function of the detectable mass for a number of the largest HI surveys. |
One of the larger surveys illustrated in Figure 11 consists of off scans made in the course of studying cataloged galaxies as was discussed earlier. The "Off Scan" line represents an estimate of the volume covered in calibration scans by an assortment of Arecibo surveys primarily by myself and by Giovanelli & Haynes and collaborators. It is notable that only a few objects were picked up in these off scans, while Henning (1992) detected 37 objects in an almost identical search volume. Part of this difference is because these off scan surveys do not usually make note of previously cataloged galaxies that are accidentally detected, and they have also been quite unsuccessful at identifying low mass objects, probably because of the failure to distinguish narrow HI features from interference. It seems clear that despite their "serendipity potential," off scan surveys do not match the power of systematic surveys.
The diagram shows that the high mass end of the luminosity function has been probed fairly well, but the volumes studied at low masses are substantially smaller. The Henning survey is one of the best for a wide range of mass sensitivity, but unfortunately (for our purposes) it was mostly carried out at low Galactic latitudes where optical extinctions are large so that it is difficult to compare optical and 21 cm results. Another point not made by this graph is that the VLA survey by Weinberg et al. (1991) examines a realm of small angular sizes and separations that the other surveys are insensitive to because of confusion. Thus they are able to detect low mass companions to massive galaxies where the single dish surveys might simply assume the gas was part of the larger galaxy.
The recent surveys conducted by Henning (1992) and by Weinberg et al. (1991) do demonstrate the presence of a significant number of low mass HI sources. However, the relatively small number of new objects found by these surveys does not allow the HI luminosity function to be determined well for low masses. A deeper survey using the largest radio telescope available, the 305 m diameter Arecibo telescope, was the logical extension of their work. This survey is described in the next section, and its volume/mass function is illustrated in Figure 11.