A. MONTE CARLO ESTIMATES OF REDDENING AND UNDERLYING BALMER ABSORPTION

Here we would like to describe the Monte Carlo procedure we use for determining the corrections for reddening and underlying stellar absorption in the Hydrogen lines. Beginning with an observed line flux F(), and an equivalent width W(), we can parameterize the correction for underlying stellar absorption as

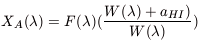
(A1)

The parameter a_HI is expected to be relatively insensitive to wavelength because all of the Balmer lines should be saturated in the stars which are producing the underlying continuum. As described in section 2, the reddening correction is applied to determine the intrinsic line intensity I() relative to H

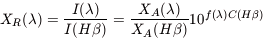
(A2)

We assume the intrinsic Balmer line ratios calculated by Hummer & Storey (1987), and we use the reddening function, f(), normalized at H, from the Galactic reddening law of Seaton (1979), as parameterized by Howarth (1983), assuming a value of R A_V / E_{B - V} = 3.2. By comparing X_R() to theoretical values, X_T(), we determine the parameters a_HI and C(H) self consistently, and run a Monte Carlo over the input data to test the robustness of the solution and to determine the systematic uncertainty associated with these corrections.

For definiteness, we list here the theoretical ratios we use:

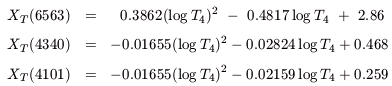
(A3)

where the temperature is T₄ = T/10⁴K. The values for f() we take are

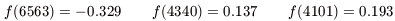
(A4)

We begin therefore with four input fluxes F() along with their associated observational (statistical) uncertainties and four equivalent widths (and their observational uncertainties). In addition, the theoretical ratios are temperature dependent, so we must add the temperature and its uncertainty as an additional observational input. From these, the ratios, X_R() for H, H, and H are obtained. The ² statistic is defined by

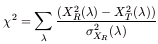
(A5)

where _XR() is the derived uncertainty in X_R. The minimization of ², allows us to determine the values of a_HI and C(H). The uncertainties in the two outputs are determined by varying the solution so that ²(a ± _a) - ²(a) = 1. _C(H) is similarly determined.

As we indicated above, we further test this solution and its robustness by running a Monte Carlo on the input data. This also allows us to better determine the systematic uncertainty in the output parameters a_HI and C(H). The data for the Monte Carlo are generated from the input data, F(), W() and temperature and the uncertainties in these quantities. A Gaussian distribution of input values centered on the observed values with a spread determined by their observational uncertainties. A new set of data is then randomly generated by picking input values from these Gaussian distributions. Consequently, after running the ² minimization procedure, new values for the output parameters a_HI and C(H) are found. Our Monte Carlo produces 1000 randomly generated data sets from which we can produce a distribution of solutions for a_HI and C(H). One would expect that the mean of the solutions for a_HI and C(H) tracks the original solution based on the actual observational data. The spread in these allows us to test the systematic uncertainty associated with these quantities.