


We have learned a great deal about the large-scale structure of the
Universe from the redshift surveys discussed in preceding chapters.
In these surveys we have generally taken the measured redshift cz as
a distance indicator, enabling us to construct three-dimensional maps
of the distribution of galaxies. We have also gone one step beyond
this, combining theory with observations to use the redshift maps as a
means of studying the origin of large scale structure, and the value
of the cosmological density parameter
 0. These analyses
have
been premised on the gravitational instability paradigm, according to
which structure grows due to gravitational amplification of initial
density perturbations (Section 2.2). But
redshift
measurements do not, by themselves, lead to a conclusive test of the
gravitational instability paradigm. Such a test requires the
additional information we gain from what we broadly refer to as
peculiar velocity surveys.
0. These analyses
have
been premised on the gravitational instability paradigm, according to
which structure grows due to gravitational amplification of initial
density perturbations (Section 2.2). But
redshift
measurements do not, by themselves, lead to a conclusive test of the
gravitational instability paradigm. Such a test requires the
additional information we gain from what we broadly refer to as
peculiar velocity surveys.
The limitations of redshift surveys stem from their inability to separate the two contributions to a galaxy's observed redshift: the cosmological component associated with the expansion of the Universe, and the peculiar component associated with the galaxy's proper motion with respect to the local rest frame (see Eq. 2). Such a separation is possible only if, in addition to the redshift cz, one has a redshift-independent distance measurement d. Peculiar velocity surveys are based on data sets consisting of redshifts and redshift-independent distance measurements, or "redshift-distance samples." From these two measurements one readily obtains the radial component of each galaxy's peculiar velocity,
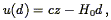
| (147) |
where we have used Eq. (2) and defined
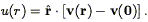
| (148) |
Note it is only the radial component of the peculiar velocity that we can measure. We discuss an indirect means of reconstructing the transverse components of the peculiar velocity field in Section 7.5 below.
The gravitational instability paradigm requires that the linear peculiar velocity and density fluctuation fields be related to one another according to the local expression Eq. (30), or the global expression Eq. (33). Those formulations of the velocity-density relation contain the Hubble constant H0. In actual peculiar velocity analyses, explicit dependence on the Hubble constant is avoided, by working in a system of units in which distances are expressed as velocities - i.e., in which the Hubble constant is defined to be unity. Eqs. (30) and (33) also involve actual mass density fluctuations, whereas redshift surveys provide galaxy density fluctuations only. We thus rewrite the two equations as they appear in an actual analysis:
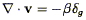
| (149) |
and
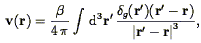
| (150) |
where  =
f(
=
f( 0,
0,
 ) / b (Eq. 51) and
b is the
biasing parameter. It is understood that the derivatives in
Eq. (149) and the integral in Eq. (150) are
with respect to spatial variables expressed in km s-1.
) / b (Eq. 51) and
b is the
biasing parameter. It is understood that the derivatives in
Eq. (149) and the integral in Eq. (150) are
with respect to spatial variables expressed in km s-1.
A proper analysis of redshift-distance samples will yield
v(r), while we derive
 g(r) from
redshift survey
data. We can thus test the validity of the gravitational instability
paradigm by seeing whether these fields obey Eqs. (149)
and (150) (20) .
Furthermore, to the extent that
the data are consistent with the gravitational instability picture,
the ratio of the galaxy density and velocity divergence fields gives a
direct measure of
g(r) from
redshift survey
data. We can thus test the validity of the gravitational instability
paradigm by seeing whether these fields obey Eqs. (149)
and (150) (20) .
Furthermore, to the extent that
the data are consistent with the gravitational instability picture,
the ratio of the galaxy density and velocity divergence fields gives a
direct measure of  . Indeed,
with data of sufficient quality
and quantity, we might hope eventually to go beyond the linear
velocity-density relations, and thus break the degeneracy between
. Indeed,
with data of sufficient quality
and quantity, we might hope eventually to go beyond the linear
velocity-density relations, and thus break the degeneracy between
 0 and b.
0 and b.
While confirmation of the gravitational instability picture and
determination of
 0 are their most
important goals, peculiar
velocity surveys serve other purposes as well. One is to characterize
the mass distribution on very large scales. Because of shot noise,
existing wide-angle redshift surveys cannot accurately measure number
density fluctuations at distances much greater than ~ 15,000 km
s-1. However, large-amplitude
(
0 are their most
important goals, peculiar
velocity surveys serve other purposes as well. One is to characterize
the mass distribution on very large scales. Because of shot noise,
existing wide-angle redshift surveys cannot accurately measure number
density fluctuations at distances much greater than ~ 15,000 km
s-1. However, large-amplitude
( 500 km
s-1) coherent peculiar
velocities on very large scales can be detected at such distances with
relatively modest samples (e.g.,
Lauer & Postman
1994
;
Dekel 1994).
Velocity perturbations drop off more slowly with increasing scale than
do density perturbations, as we saw in
Fig. 1; mass
density fluctuations of a few percent on a 20,000 km s-1
scale - undetectable in present redshift surveys - can give rise to
detectable bulk motions if
500 km
s-1) coherent peculiar
velocities on very large scales can be detected at such distances with
relatively modest samples (e.g.,
Lauer & Postman
1994
;
Dekel 1994).
Velocity perturbations drop off more slowly with increasing scale than
do density perturbations, as we saw in
Fig. 1; mass
density fluctuations of a few percent on a 20,000 km s-1
scale - undetectable in present redshift surveys - can give rise to
detectable bulk motions if
 0 is not much
less than unity.
For this reason, peculiar velocity measurements constitute one of the
best methods of measuring mass density fluctuations on very large
scales; this quality makes them a powerful discriminant of rival
cosmogonic theories (Section 7.1).
0 is not much
less than unity.
For this reason, peculiar velocity measurements constitute one of the
best methods of measuring mass density fluctuations on very large
scales; this quality makes them a powerful discriminant of rival
cosmogonic theories (Section 7.1).
A related virtue of peculiar velocity surveys is their capacity to
reveal mass fluctuations independently of bias. Through redshift
surveys we can map the number density fluctuations
 g, and
derive the mass density field
g, and
derive the mass density field
 through an assumed
model of bias. But if the relationship between luminous and dark mass
is, in reality, far different from the linear model we usually
adopt - or worse, if that relationship has large variance
(Cen & Ostriker
1992b)
or is stochastic - redshift surveys may in fact tell
us little about mass fluctuations. If the gravitational instability
picture is valid, however, peculiar velocities uniquely reflect the
mass density field. This point has been emphasized in recent years by
Dekel, Bertschinger, and coworkers (e.g.,
Bertschinger & Dekel
1989
;
Dekel et al. 1990;
Dekel 1994),
who have developed a method to
reconstruct the mass density field from peculiar velocity measurements
(Section 7.5).
through an assumed
model of bias. But if the relationship between luminous and dark mass
is, in reality, far different from the linear model we usually
adopt - or worse, if that relationship has large variance
(Cen & Ostriker
1992b)
or is stochastic - redshift surveys may in fact tell
us little about mass fluctuations. If the gravitational instability
picture is valid, however, peculiar velocities uniquely reflect the
mass density field. This point has been emphasized in recent years by
Dekel, Bertschinger, and coworkers (e.g.,
Bertschinger & Dekel
1989
;
Dekel et al. 1990;
Dekel 1994),
who have developed a method to
reconstruct the mass density field from peculiar velocity measurements
(Section 7.5).
The use of redshift-distance samples as described above appears
straightforward in principle. In reality, redshift-independent
distances are far too inaccurate for Eq. (147) to be applied
as written to real data. Much of the complexity (and controversy)
surrounding peculiar velocity surveys arises from the steps needed to
account for the consequences of distance measurement errors. In what
follows we describe how workers in the field have attempted to deal
with this complexity, and discuss the issues that remain
unresolved. Still, it is worth emphasizing at the outset our optimism
about the program of comparing the peculiar velocity and galaxy
density fields in order to estimate
 . Much progress has been
made to date using existing large, fairly complete redshift-distance
samples, and still larger and improved redshift-distance samples will
soon become available. Redshift survey data yielding
. Much progress has been
made to date using existing large, fairly complete redshift-distance
samples, and still larger and improved redshift-distance samples will
soon become available. Redshift survey data yielding
 g(r)
for the local region are similarly improving. We consider it likely
that within a decade or so, peculiar velocity analyses will have
provided not only convincing substantiation of the gravitational
instability picture, but also a believable estimate of
g(r)
for the local region are similarly improving. We consider it likely
that within a decade or so, peculiar velocity analyses will have
provided not only convincing substantiation of the gravitational
instability picture, but also a believable estimate of
 , and
quite possibly, further insights into the subtle relationship between
luminous and dark mass.
, and
quite possibly, further insights into the subtle relationship between
luminous and dark mass.
We begin this chapter with a discussion of distance indicator
relations, with emphasis on the Tully-Fisher and
Dn- relations
for spiral and elliptical galaxies, respectively.
Section 6.2
briefly discusses the evidence we have that these distance indicator
relations are universal, and Section 6.3 covers other
distance indicator relations that are likely to become important in
coming years. The rest of the chapter is devoted to the types of
analyses one does with peculiar velocity data, emphasizing the
inherent pitfalls and biases. This is first done at a qualitative
level in Section 6.4, followed by a mathematical
treatment
in Section 6.5. The scientific results of peculiar
velocity work are discussed in Chapters 7
and 8.
relations
for spiral and elliptical galaxies, respectively.
Section 6.2
briefly discusses the evidence we have that these distance indicator
relations are universal, and Section 6.3 covers other
distance indicator relations that are likely to become important in
coming years. The rest of the chapter is devoted to the types of
analyses one does with peculiar velocity data, emphasizing the
inherent pitfalls and biases. This is first done at a qualitative
level in Section 6.4, followed by a mathematical
treatment
in Section 6.5. The scientific results of peculiar
velocity work are discussed in Chapters 7
and 8.
6.1. Galaxian Distance Indicator Relations
We obtain redshift-independent galaxy distances by means of distance-indicator relations, or DIs. The essence of a DI is an empirical correlation between two intrinsic properties of a galaxy, one of which is distance-dependent (e.g., diameter) and one of which is distance-independent (e.g., surface brightness). (21) Thus, for example, surface brightness might be known to correlate with absolute diameter; a comparison of the measured angular diameter with the inferred absolute diameter, obtained from this correlation, yields a distance estimate. In some cases the distance-independent property is simply the identification of an object as belonging to a particular class, such as Type 1a Supernovae (Section 6.3.3); in that case a DI may be called a "standard candle" or a "standard ruler," according to whether the distance-dependent property is luminosity or diameter.
Long before their use in peculiar velocity surveys, DIs were employed
in the quest to measure the Hubble constant H0 and the
acceleration parameter q0 (e.g.,
Weinberg 1972).
Determination of H0 requires
absolute calibration of a DI, which involves referencing DI
measurements to a set of fiducial galaxies whose distances in Mpc
are known. For peculiar velocity work, absolute calibration is
unnecessary; the DI measurements are instead referenced to a fiducial
set whose distances in km s-1 are known. (We discuss how this
is done
in practice in Section 7.2.) In this
review, we
specifically do not discuss efforts to absolutely calibrate DIs and
apply them toward determination of H0; this subject
has been recently reviewed by
Jacoby et
al. (1992) .
Estimation of q0 does
not require absolute calibration, but does entail observations of
galaxies at substantial (z
 0.2) redshifts. The
peculiar
velocity surveys we will discuss are strictly confined to
z
0.2) redshifts. The
peculiar
velocity surveys we will discuss are strictly confined to
z  0.06 and
thus have no bearing on the q0 problem.
0.06 and
thus have no bearing on the q0 problem.
While many empirical correlations between distance-independent and distance-dependent galaxian properties exist, not all are equally useful as DIs. In what follows, we describe in detail those DIs which have been most fruitfully applied to the study of peculiar velocities, as well as some likely to be so employed in the future.
Both elliptical and spiral galaxies show correlations between galaxian luminosity and a relevant measure of internal velocity dispersion. In Section 6.1.1, we discuss this correlation for spirals, the Tully-Fisher (TF) relation; Section 6.1.2 discusses the corresponding correlation for ellipticals.
6.1.1. The Tully-Fisher Relation for Spiral Galaxies
Ordinary spiral galaxies are, for practical purposes, the most suitable objects to use as tracers of the peculiar velocity field in the local Universe. They are more numerous and more uniformly distributed than their luminous counterparts, ordinary elliptical galaxies (which tend to congregate in the cores of dense clusters). They are also bright enough to be carefully studied at fairly large distances, unlike the still more numerous but faint dwarf galaxies. As a result, the TF relation, which is the main DI for spirals, has been the workhorse in peculiar velocity surveys to date.
Since spiral galaxies are flattened systems supported by rotation, the relevant measure of internal velocity for Tully-Fisher is rotation velocity. Because spiral galaxies have "flat" rotation curves, their rotation velocities are well-defined, as we discuss below. In practice, the luminosity-rotation velocity correlation is well modeled as a power law,
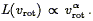
| (151) |
Using the conventional notation of astronomers, which we will follow here, this equation may be rewritten
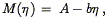
| (152) |
where M = const. - 2.5log L is the absolute magnitude, and
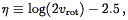
| (153) |
where vrot is measured in
km s-1, is a convenient logarithmic
measure of the rotation velocity. The normalization of
 is such
that its value lies roughly between ± 0.3 for most spirals. The
quantities A and b are known as the "zeropoint" and "slope" of
the TF relation; the slope is found to lie in the range b ~ 5-10,
depending on the details of how
vrot and M are
measured. Thus, the power-law exponent of the luminosity-rotation
velocity relation is
is such
that its value lies roughly between ± 0.3 for most spirals. The
quantities A and b are known as the "zeropoint" and "slope" of
the TF relation; the slope is found to lie in the range b ~ 5-10,
depending on the details of how
vrot and M are
measured. Thus, the power-law exponent of the luminosity-rotation
velocity relation is
 ~ 2-4. The apparent
magnitude
m of a galaxy is the observed quantity; it is related to the
absolute magnitude via the inverse-square law:
~ 2-4. The apparent
magnitude
m of a galaxy is the observed quantity; it is related to the
absolute magnitude via the inverse-square law:
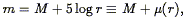
| (154) |
which defines the distance modulus µ(r).
The measurement of rotation velocities in TF studies has been carried
out mainly through analysis of HI 21 cm profiles,
especially prior
to 1990. These profiles are derived from spatially unresolved data,
and therefore do not give rotation velocity per se, but rather
total 21 cm intensity as a function of velocity. This has led to a
variety of efforts to define a 21 cm profile width which most
faithfully reflects rotation velocity (e.g.,
Tully & Fouqué
1985
;
Aaronson et al. 1986
;
Bicay & Giovanelli
1986a ,
b).
In recent years
some workers have employed optical measures of rotation
velocity, measured from the H emission line
(Dressler & Faber
1990b
;
Courteau 1992
;
Mathewson et al. 1992a,
b;
Mathewson & Ford
1994),
using a long slit oriented along the major
axis of the galaxy. Such measurements have become increasingly useful
as TF studies have been extended to the Southern Hemisphere, where
fewer radio telescopes exist, and to larger distances, where confusion
and sensitivity problems become severe in the radio. An alternative
is to employ imaging Fabry-Perot spectroscopy in the
H
emission line
(Dressler & Faber
1990b
;
Courteau 1992
;
Mathewson et al. 1992a,
b;
Mathewson & Ford
1994),
using a long slit oriented along the major
axis of the galaxy. Such measurements have become increasingly useful
as TF studies have been extended to the Southern Hemisphere, where
fewer radio telescopes exist, and to larger distances, where confusion
and sensitivity problems become severe in the radio. An alternative
is to employ imaging Fabry-Perot spectroscopy in the
H line
(Schommer et al. 1993),
which allows one to map out the rotation
velocity field in two-dimensional detail. The optical, unlike the
HI,
measurements are spatially resolved. Because 21 cm and optical
measures of rotation can differ systematically
(Tully &
Fouqué 1985
;
Pierce & Tully
1988),
it cannot be assumed that the slope or zeropoint of the
HI and optical TF relations will be the same;
recent work on combining the two types of data have addressed this issue
(Mathewson et
al. 1992b;
Willick et al. 1995b).
line
(Schommer et al. 1993),
which allows one to map out the rotation
velocity field in two-dimensional detail. The optical, unlike the
HI,
measurements are spatially resolved. Because 21 cm and optical
measures of rotation can differ systematically
(Tully &
Fouqué 1985
;
Pierce & Tully
1988),
it cannot be assumed that the slope or zeropoint of the
HI and optical TF relations will be the same;
recent work on combining the two types of data have addressed this issue
(Mathewson et
al. 1992b;
Willick et al. 1995b).
Regardless of how velocity width is measured, the raw measurement differs from the true width (which enters into the TF relation) because of projection on the sky. The true width is estimated by dividing the raw value by the sine of the estimated inclination angle of the galaxy, obtained from the ellipticity of its optical image.
The existence of a correlation between optical luminosity and HI velocity width had been recognized since at least the early 1970s (see, for example, Bottinelli et al. 1971 ; Balkowski et al. 1973 ; Sandage & Tammann 1976), but Tully & Fisher (1977) were the first to characterize this correlation by the linear relation (Eq. 152), finding a slope b ~ 6. Their work brought its potential for use as an important cosmological tool to the attention of the astronomical community. Early work with the TF relation used blue-bandpass (B) measurements of luminosity, which were by far the most readily available in the late 1970s. It was recognized early on, however, that such measurements were subject to extinction of starlight by dust in both the source galaxy and in our own Galaxy. These effects represented systematic uncertainties in early applications of the TF relation.
An important advance was made in the late 1970's and early 1980's
through the work of Aaronson and collaborators (e.g.,
Aaronson, Huchra, &
Mould 1979
;
Aaronson et al. 1982a,
b).
They recognized that
long-wavelength photometry would suffer less from internal and
Galactic extinction than B band photographic or photoelectric data.
The Aaronson group undertook a program of photoelectric H band
( = 1.6µm)
photometry of spiral galaxies in the Local
Supercluster. These measurements were made through apertures whose
size was dictated by instrumental constraints, and were subsequently
scaled to a fiducial aperture roughly one-third the optical size of
the galaxy. This awkward procedure was a drawback of the method, but
the Aaronson group nonetheless found that the new infrared TF relation
(IRTF) was tighter than the older short-wavelength version. They also
found that the IRTF required little or no correction for internal and
Galactic extinction, and that its slope b was almost exactly 10,
corresponding to a power-law exponent
= 1.6µm)
photometry of spiral galaxies in the Local
Supercluster. These measurements were made through apertures whose
size was dictated by instrumental constraints, and were subsequently
scaled to a fiducial aperture roughly one-third the optical size of
the galaxy. This awkward procedure was a drawback of the method, but
the Aaronson group nonetheless found that the new infrared TF relation
(IRTF) was tighter than the older short-wavelength version. They also
found that the IRTF required little or no correction for internal and
Galactic extinction, and that its slope b was almost exactly 10,
corresponding to a power-law exponent
 = 4.
= 4.
The v4rot dependence of the IRTF was seen as favorable for two reasons. First, as we discuss further below, it drops out naturally from a simple theoretical "derivation" of the TF relation based on considerations of centrifugal equilibrium. Second, a v4 power law also described the analogous Faber-Jackson relation for elliptical galaxies (Section 6.1.2). Since elliptical galaxies generally lack ongoing star formation, their radiant output in the blue is produced by an old stellar population. The blue-light luminosities of spiral galaxies, by contrast, may in some cases be dominated by the hot, massive stars which result from recent bursts of star formation. Aaronson et al. (1979) suggested that the H band photometry measured the light of the old stellar population, presumably the most faithful tracer of the mass, and therefore correlated better with the gravitational potential - and through it, the observed rotation velocity. The agreement in slope with that of the Faber-Jackson relation seemed to confirm this notion.
Attempts to explain the TF relation in terms of the composition and dynamics of spiral galaxies begin with the equation of centrifugal equilibrium,
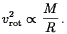
| (155) |
If one then assumes a universal mass-to-light ratio (M/L),
and a constant mean surface brightness
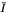 for spirals, so that
for spirals, so that
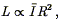
| (156) |
one obtains
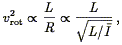
| (157) |
or
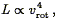
| (158) |
precisely the exponent characterizing the IRTF. Aaronson et al. (1979) cited this consistency as evidence that the near-infrared TF relation was more fundamental than shorter wavelength versions.
While this explanation of the TF slope is not unreasonable, plausible
"derivations" of quite different slopes have been presented. For
example,
Sandage & Tammann
(1976)
began with Eq. (155),
and also invoked the presumed constancy of (M/L). They
then supposed
that the characteristic radius R at which the equation is to be
interpreted is independent of luminosity, on average. This yields
L  vrot2, corresponding to a TF slope b
= 5, similar to the earliest estimates for the B bandpass
(Tully & Fisher
1977
;
Bottinelli et al. 1983).
Moreover,
Burstein (1982)
has argued on the
basis of the observed slope of the TF relation and the relation
between surface brightness and rotation velocity, that the assumption
of a uniform mass-to-light ratio cannot hold true. The notion that
one can straightforwardly derive the TF slope from first principles is
now, in fact, considered dubious. It has become clear that the TF
slope has more to do with technical issues of measurement than with
the constancy of mass-to-light ratios or surface brightnesses. In
particular, the size of the aperture and the photometric bandpass used
materially affect the observed slope
(Bottinelli et al. 1983
;
Pierce & Tully 1988
;
Willick 1991
;
Jacoby et al. 1992
;
cf. Fig. 12).
Bernstein et al. (1994)
,
for example, found
an H band TF slope of ~ 6, rather than the canonical 10, when they
used large apertures which encompassed essentially all of the light
from a galaxy. Moreover, the assumption that spirals possess constant
(M/L) in H band light, has been challenged.
Bothun (1986)
,
for example, has pointed out that small variations in heavy-element
abundances can greatly alter the infrared energy output of a stellar
population, in which case the age of a galaxy should affect
(M/L).
Pierce (1988,
1991)
has shown that, as measured in I band
light, (M/L) ratios show strong variations with
luminosity. In
short, it appears that poorly understood issues pertaining to the
nature and spatial distribution of stellar populations will be central
to an eventual understanding of the TF relation.
vrot2, corresponding to a TF slope b
= 5, similar to the earliest estimates for the B bandpass
(Tully & Fisher
1977
;
Bottinelli et al. 1983).
Moreover,
Burstein (1982)
has argued on the
basis of the observed slope of the TF relation and the relation
between surface brightness and rotation velocity, that the assumption
of a uniform mass-to-light ratio cannot hold true. The notion that
one can straightforwardly derive the TF slope from first principles is
now, in fact, considered dubious. It has become clear that the TF
slope has more to do with technical issues of measurement than with
the constancy of mass-to-light ratios or surface brightnesses. In
particular, the size of the aperture and the photometric bandpass used
materially affect the observed slope
(Bottinelli et al. 1983
;
Pierce & Tully 1988
;
Willick 1991
;
Jacoby et al. 1992
;
cf. Fig. 12).
Bernstein et al. (1994)
,
for example, found
an H band TF slope of ~ 6, rather than the canonical 10, when they
used large apertures which encompassed essentially all of the light
from a galaxy. Moreover, the assumption that spirals possess constant
(M/L) in H band light, has been challenged.
Bothun (1986)
,
for example, has pointed out that small variations in heavy-element
abundances can greatly alter the infrared energy output of a stellar
population, in which case the age of a galaxy should affect
(M/L).
Pierce (1988,
1991)
has shown that, as measured in I band
light, (M/L) ratios show strong variations with
luminosity. In
short, it appears that poorly understood issues pertaining to the
nature and spatial distribution of stellar populations will be central
to an eventual understanding of the TF relation.
Beyond this, there is a fatal flaw in any simple model of the TF relation based on the equation of centrifugal support. Spiral galaxies possess roughly exponential light profiles (Freeman 1970) with a characteristic scale length. However, they have rotation curves which rise quickly from zero to a characteristic rotation speed that is observed to be remarkably constant out to many exponential scale lengths (e.g., Rubin et al. 1980, 1982, 1985). This constancy of the rotation speed is one of the main pieces of evidence for the existence of dark halos in spiral galaxies (Faber & Gallagher 1979). Indeed, it is only because of such flat rotation curves that a well-defined rotation velocity of spiral galaxies exists. Thus the characteristic scale of the mass distribution in spiral galaxies is appreciably larger than is that of the light, although the two were equated in Eqs. (155)-(157). Moreover, the TF relation applies equally well to all galaxies of a given rotation speed, although their exponential scale lengths, as well as their bulge-to-disk ratios and morphologies, may vary considerably (Han 1991 ; Willick 1991). Evidently, there is a complex interplay between luminous and dark mass which determines the final state of spiral galaxies. While some progress has been made toward understanding these effects (e.g., Blumenthal et al. 1986), our understanding of the physical basis of the TF relation remains schematic at best. The origin of the TF relation is shrouded in the mysteries of spiral galaxy formation.
With the advent of CCD detectors in the 1980s, highly accurate galaxy
photometry has become routine. Two-dimensional digital detectors such
as CCDs permit one to tailor the photometric aperture to the galaxy
image in a natural way, in contrast to the somewhat arbitrary scalings
required in fixed-aperture photoelectric photometry. CCDs are very
sensitive in the R ( ~
0.7µm) and I (
~
0.7µm) and I ( ~ 0.8µm) bandpasses, and most recent TF studies have been
carried out in one of these bands
(Bothun & Mould 1987
;
Pierce & Tully 1988
;
Willick 1991
;
Han 1991
;
Courteau 1992
;
Mathewson et al. 1992a,
b;
Roth 1993
;
Mould et al. 1993
;
Mathewson & Ford
1994
;
Haynes et al. 1995).
Dust extinction is less of a problem in R or I
than in B, though not negligible as it is at 1.6µm (a detailed
discussion of models of internal extinction is given by
Giovanelli et
al. 1994).
With the advent of imaging detectors sensitive at ~ 2µm, a
few workers are returning to the near infrared for TF work
(Peletier & Willner
1993
;
Bernstein et al. 1994).
~ 0.8µm) bandpasses, and most recent TF studies have been
carried out in one of these bands
(Bothun & Mould 1987
;
Pierce & Tully 1988
;
Willick 1991
;
Han 1991
;
Courteau 1992
;
Mathewson et al. 1992a,
b;
Roth 1993
;
Mould et al. 1993
;
Mathewson & Ford
1994
;
Haynes et al. 1995).
Dust extinction is less of a problem in R or I
than in B, though not negligible as it is at 1.6µm (a detailed
discussion of models of internal extinction is given by
Giovanelli et
al. 1994).
With the advent of imaging detectors sensitive at ~ 2µm, a
few workers are returning to the near infrared for TF work
(Peletier & Willner
1993
;
Bernstein et al. 1994).
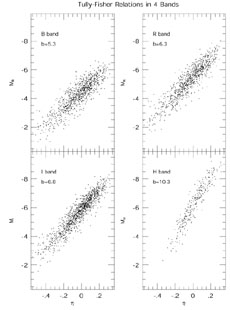
In Fig. 12 we plot B, R, and I TF relations obtained from the large data set of Mathewson et al. (1992b), and an H band TF relation from the Aaronson et al. (1982b) data set, as updated by Tormen & Burstein (1994, 1995). In each case a Hubble flow model of distances has been used; thus, the diagrams contain extra scatter due to the inaccuracy of the distance assignments, as discussed below. Nonetheless, the relation is well defined in all of the bandpasses, although the scatter in the R, I and H bandpasses is noticeably smaller than in the B bandpass. The B and R band data are photoelectric measurements taken from the RC3 and Lauberts & Valentijn (1989) catalogs, respectively, as compiled by D. Burstein (private communication). The slopes of the fitted TF relations are indicated in the figure; these TF fits are corrected for sample selection bias as described in Section 6.5. As can be seen, the slope increases with increasing wavelength. The very large change from I to H is due only partially to wavelength increase; it stems mainly from the small apertures within which the H band magnitudes are measured (the I band magnitudes are "total" magnitudes) and the different definitions of velocity width used by Mathewson et al. vs. Aaronson et al.In all cases, the absolute magnitudes are expressed in the units suitable to peculiar velocity work, in which distances are measured in km s-1.
|
Figure 12. TF relations in the B, R, I, and H bandpasses. The B, R, and I TF relations are obtained from the data set of Mathewson et al. (1992b). The B and R magnitudes for the Mathewson galaxies are photoelectric measurements obtained from the RC3 and Lauberts-Valentijn (1989) catalogs respectively; the I band magnitudes are from the CCD photometry, and the velocity widths from a combination of HI and optical measurements, carried out by the Mathewson group. The H band magnitudes are from the local sample of Aaronson et al. (1982b) , as updated by Tormen & Burstein (1994, 1995). In each case the plotted absolute magnitudes are computed as M = m - 5log(cz), where cz is the observed redshift, and are thus expressed in the units appropriate to peculiar velocity studies. Further details are given in the text. |
An important and unresolved issue is the rms scatter of galaxies
around the mean TF relation, usually quoted in magnitude units and
denoted  . The earliest
estimates of the TF scatter were
. The earliest
estimates of the TF scatter were
 ~ 0.5-0.6 mag in B
(Tully & Fisher
1977).
The Aaronson group later found a somewhat tighter correlation,
~ 0.5-0.6 mag in B
(Tully & Fisher
1977).
The Aaronson group later found a somewhat tighter correlation,

 0.45-0.50 mag, in the near
infrared (e.g.,
Aaronson et al. 1986).
However, Sandage, Tammann, and coworkers were critical of these
relatively low estimates, arguing that sample selection effects
(Section 6.4) were introducing gross biases into
estimates
of the scatter. By enlarging the data sets studied by the Aaronson
group in the Virgo cluster,
Sandage (1988)
and
Kraan-Korteweg,
Cameron, & Tammann (1988)
derived values ranging from ~ 0.7-1.0 mag, although
Fukugita, Okamura,
& Yasuda (1993)
explain much of this
increased scatter as due to appreciable depth effects in the
cluster. More recently,
Federspiel, Sandage,
& Tammann (1994)
have claimed that while the most luminous galaxies may have
0.45-0.50 mag, in the near
infrared (e.g.,
Aaronson et al. 1986).
However, Sandage, Tammann, and coworkers were critical of these
relatively low estimates, arguing that sample selection effects
(Section 6.4) were introducing gross biases into
estimates
of the scatter. By enlarging the data sets studied by the Aaronson
group in the Virgo cluster,
Sandage (1988)
and
Kraan-Korteweg,
Cameron, & Tammann (1988)
derived values ranging from ~ 0.7-1.0 mag, although
Fukugita, Okamura,
& Yasuda (1993)
explain much of this
increased scatter as due to appreciable depth effects in the
cluster. More recently,
Federspiel, Sandage,
& Tammann (1994)
have claimed that while the most luminous galaxies may have
 = 0.4
mag, the TF scatter for a typical galaxy is ~ 0.6-0.7 mag.
= 0.4
mag, the TF scatter for a typical galaxy is ~ 0.6-0.7 mag.
On the other hand, recent years have seen ever-decreasing estimates of the TF scatter by groups employing CCD photometry. Bothun & Mould (1987) suggested that an appropriate adjustment of the photometric aperture with rotation velocity width could reduce the scatter of the I band TF relation to ~ 0.20-0.25 mag. Pierce & Tully (1988) observed a scatter in the nearby Ursa Major cluster of ~ 0.30 mag, and calculated that the contribution of true cluster depth was such that the true scatter was 0.25 mag. Willick (1990, 1991) studied a sample of relatively distant clusters and found an R band scatter of ~ 0.30 mag. Courteau (1992) identified a region of "quiet Hubble flow" within a larger field sample in which the R band TF scatter was 0.32 mag. Schommer et al. (1993) found a scatter of 0.25-0.3 mag for their I band Fabry-Perot sample (see above). Very recently, Bernstein et al. (1994) have studied a carefully selected I band CCD sample in the Coma Supercluster region which exhibits an apparent TF scatter of ~ 0.10 mag.
The observed TF scatter comes from three sources: intrinsic or
"cosmic" scatter, photometric and velocity width measurement errors,
and incorrect distance assignments. Cosmic scatter is the quantity of
greatest interest astrophysically; because of uncertainties in the
other two sources of scatter, however, it is not well-constrained at
present. Photometric errors per se are very small
( 0.05 mag) when CCDs
are used. However, the extinction corrections
made to the apparent magnitudes, while accurate in the mean, may be
incorrect by ~ 0.1 mag in individual cases due to variations in the
dust content of spiral galaxies. Raw velocity width measurements
contain ~ 5% errors, and comparable errors are incurred in making
the inclination correction; resulting errors in the width parameter
0.05 mag) when CCDs
are used. However, the extinction corrections
made to the apparent magnitudes, while accurate in the mean, may be
incorrect by ~ 0.1 mag in individual cases due to variations in the
dust content of spiral galaxies. Raw velocity width measurements
contain ~ 5% errors, and comparable errors are incurred in making
the inclination correction; resulting errors in the width parameter
 must then be
multiplied by the TF slope. Overall, measurement
errors can account for ~ 0.15-0.30 mag, depending on bandpass,
inclination, and quality of the HI or optical width
determination. Cosmic scatter and measurement errors, added in
quadrature, are what the quantity
must then be
multiplied by the TF slope. Overall, measurement
errors can account for ~ 0.15-0.30 mag, depending on bandpass,
inclination, and quality of the HI or optical width
determination. Cosmic scatter and measurement errors, added in
quadrature, are what the quantity
 is meant to
signify. However, when a TF sample is used to estimate scatter,
galaxies must be assigned distances; errors in these assignments
contribute to the observed scatter. Minimizing this last
contribution, and subtracting it from the observed scatter, is a
tricky but necessary part of estimating the true TF scatter.
is meant to
signify. However, when a TF sample is used to estimate scatter,
galaxies must be assigned distances; errors in these assignments
contribute to the observed scatter. Minimizing this last
contribution, and subtracting it from the observed scatter, is a
tricky but necessary part of estimating the true TF scatter.
The observed value of the TF scatter is important not only in determining the size of random errors, but also of systematic errors due to statistical bias effects (Section 6.4). The discrepancy among estimates of the TF scatter discussed above probably arises from a combination of two factors: small number statistics, and different approaches to the problem of distance assignment errors. Large TF residuals that one author attributes to an erroneous distance model, such as the misassignment of a galaxy to a cluster, another might attribute to true scatter. In the first case the galaxy in question would be eliminated from the analysis and a relatively small scatter obtained, while in the second it is included and a higher value results. In many cases such a decision is subjective, and may depend on the worker's own biases with regard to the true scatter. As larger and more complete samples are studied, the importance of such subjective factors will diminish, and it is likely that scatter estimates will converge. A recent study using a data set consisting of over 3000 galaxies culled from five samples (Willick et al. 1995a , b, c; cf. Section 7.2) finds the CCD R and I band scatters to be in the range 0.35-0.40 mag, and the H band scatter to be ~ 0.45 mag. A partly overlapping sample of ~ 2500 spirals analyzed by Mathewson & Ford (1994) estimated the I band scatter at 0.42 mag. Still, the issue is far from closed; claims of very small (~ 0.25 mag) scatter, large TF data sets continue to appear in the literature (e.g., Haynes et al. 1995).
6.1.2. The Faber-Jackson and Dn -
 for Elliptical
Galaxies
for Elliptical
Galaxies
The elliptical galaxy DI first used in peculiar velocity studies was
the Faber-Jackson (FJ) relation
(Faber & Jackson
1976).
Like the TF
relation, FJ expresses a power-law relationship between luminosity and
internal velocity. Unlike spirals, luminous ellipticals do not rotate
(Kormendy &
Djorgovski 1989),
and the relevant measure of internal
velocity is the rms dispersion of radial stellar velocities in the
central regions of the galaxy,
 e. Thus the FJ
relation is expressed as
e. Thus the FJ
relation is expressed as
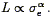
| (159) |
Unlike the case with TF, early work with FJ
(Faber & Jackson
1976
;
Schechter 1980
;
Tonry & Davis 1981)
produced reasonable agreement that the exponent of the power law was

 4, corresponding
to the infrared TF slope found by Aaronson and collaborators (see
above). However, while early estimates of the TF scatter were ~ 0.45
mag, the scatter of the FJ relation was found to be roughly twice
that. For this reason, although FJ was used with some success in
studies of the Virgocentric motion of nearby galaxies
(Schechter 1980
;
Tonry & Davis
1981),
it did not seem to hold great promise as a DI.
4, corresponding
to the infrared TF slope found by Aaronson and collaborators (see
above). However, while early estimates of the TF scatter were ~ 0.45
mag, the scatter of the FJ relation was found to be roughly twice
that. For this reason, although FJ was used with some success in
studies of the Virgocentric motion of nearby galaxies
(Schechter 1980
;
Tonry & Davis
1981),
it did not seem to hold great promise as a DI.
The situation changed dramatically when two independent groups discovered that the addition of a third parameter significantly improved the accuracy of the FJ relation (Djorgovski & Davis 1987 ; Dressler et al. 1987b (22) ). Working with newly acquired photometric and kinematic data for large samples of ellipticals, each group found that elliptical galaxies populate a planar region in a three dimensional parameter space. One expression of this fundamental plane describes the connection between the effective radius Re and the average stellar velocity dispersion and surface brightness interior to that radius:
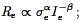
| (160) |
the dual power law maps to a plane when logarithmic quantities are
considered. The two groups both found that

 1.4,
1.4,

 0.9
(Faber et al. 1987).
When using the fundamental plane as
a DI, the 7S group preferred to incorporate the surface brightness and
radius terms into a single photometric diameter they called
Dn, the
diameter interior to which the average surface brightness attained a
fiducial value. In a subsequent study
(Lynden-Bell et
al. 1988a),
the group provided a final calibration of the new DI:
0.9
(Faber et al. 1987).
When using the fundamental plane as
a DI, the 7S group preferred to incorporate the surface brightness and
radius terms into a single photometric diameter they called
Dn, the
diameter interior to which the average surface brightness attained a
fiducial value. In a subsequent study
(Lynden-Bell et
al. 1988a),
the group provided a final calibration of the new DI:
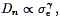
| (161) |
where the exponent

 1.20± 0.1. In this
form the modified FJ relation is known as the
Dn-
1.20± 0.1. In this
form the modified FJ relation is known as the
Dn- relation.
Dressler (1987a)
has shown that the
Dn-
relation.
Dressler (1987a)
has shown that the
Dn- relation also holds for the
bulges of early-type spirals, although this has not been exploited
beyond his initial paper.
relation also holds for the
bulges of early-type spirals, although this has not been exploited
beyond his initial paper.
Lynden-Bell et
al. (1988a)
found that the scatter in the
Dn- relation was
relation was
 0.10 dex in
logDn, corresponding to about
23% accuracy as a distance predictor. Thus,
Dn-
0.10 dex in
logDn, corresponding to about
23% accuracy as a distance predictor. Thus,
Dn- was
found to be
about twice as accurate as FJ, and compared favorably with TF. Indeed,
the 7S group used the
Dn-
was
found to be
about twice as accurate as FJ, and compared favorably with TF. Indeed,
the 7S group used the
Dn- distances to make one of the earliest
inferences of very large-scale deviation from Hubble flow
(Dressler et
al. 1987a),
as we discuss in greater detail in
Section 7.1. It is interesting to note,
however, that while
a fundamental plane led to a tighter DI, it also implied less insight
into elliptical galaxy formation. For, while a one-dimensional
relationship (such as TF) requires special conditions to be imposed at
galaxy formation, a fundamental plane is simply a reflection of
gravitational equilibrium, with the additional (albeit ill-understood;
cf. Renzini &
Ciotti 1993)
assumption that (M/L) be a function only
of the other parameters in the relation
(Faber et al. 1987
;
Gunn 1988).
Thus the fundamental plane relations tell us little more than
that elliptical galaxies are gravitationally bound structures, which
is hardly surprising.
distances to make one of the earliest
inferences of very large-scale deviation from Hubble flow
(Dressler et
al. 1987a),
as we discuss in greater detail in
Section 7.1. It is interesting to note,
however, that while
a fundamental plane led to a tighter DI, it also implied less insight
into elliptical galaxy formation. For, while a one-dimensional
relationship (such as TF) requires special conditions to be imposed at
galaxy formation, a fundamental plane is simply a reflection of
gravitational equilibrium, with the additional (albeit ill-understood;
cf. Renzini &
Ciotti 1993)
assumption that (M/L) be a function only
of the other parameters in the relation
(Faber et al. 1987
;
Gunn 1988).
Thus the fundamental plane relations tell us little more than
that elliptical galaxies are gravitationally bound structures, which
is hardly surprising.
6.2. Universality of the Distance Indicator Relations
The measurement of redshift-independent distances by
means of DIs such as TF and
Dn- assumes that
the galaxian properties they embody are universal,
i.e., independent of spatial location or local environment.
If, say, the zeropoint of the TF relation varied systematically from
one place to another, then the distances inferred from it would carry
a position-dependent error, giving rise to spurious peculiar velocity
measurements. Recognizing this, some astronomers have questioned the
reality of detections of large-scale departures from Hubble flow
(Section 7.1) - or as one
theorist asked in the provocative
title to a paper on the subject, "Is Cosmic Drift a Cosmic Myth?"
(Silk 1989).
assumes that
the galaxian properties they embody are universal,
i.e., independent of spatial location or local environment.
If, say, the zeropoint of the TF relation varied systematically from
one place to another, then the distances inferred from it would carry
a position-dependent error, giving rise to spurious peculiar velocity
measurements. Recognizing this, some astronomers have questioned the
reality of detections of large-scale departures from Hubble flow
(Section 7.1) - or as one
theorist asked in the provocative
title to a paper on the subject, "Is Cosmic Drift a Cosmic Myth?"
(Silk 1989).
Silk (1989)
suggested, on the basis of plausible (but speculative)
scenarios of galaxy formation, that both the TF and
Dn- relations would show a systematic cluster vs. field offset. Because
the DIs are typically calibrated using cluster observations, the
measured peculiar velocities of field galaxies (which dominate most
analyses of large-scale motions) might then be invalid.
de Carvalho &
Djorgovski (1992)
carried out a comparison of the properties of
field and cluster ellipticals. They argued that as measured by the
relationship between several distance-independent indices (surface
brightness, color, metallicity, and velocity dispersion) the field and
cluster galaxies differed systematically. The sense of these
differences was that field galaxies were bluer, had higher surface
brightness, and were more metal-poor than their field counterparts of
similar velocity dispersion. They proposed that these differences
would follow logically from star-formation histories if the field
ellipticals were typically younger than cluster ellipticals. A
related study was carried out by Guzmàn and coworkers
(Guzmàn 1994
;
Guzmàn & Lucey
1993
;
Guzmàn, Lucey,
& Bower 1993
;
cf.,
Gregg 1992),
who also concluded that metallicity influences the
fundamental plane relations (Section 6.1.2).
Guzmàn (1994)
explicitly argued that this "age effect" induces a significant
difference between
Dn-
relations would show a systematic cluster vs. field offset. Because
the DIs are typically calibrated using cluster observations, the
measured peculiar velocities of field galaxies (which dominate most
analyses of large-scale motions) might then be invalid.
de Carvalho &
Djorgovski (1992)
carried out a comparison of the properties of
field and cluster ellipticals. They argued that as measured by the
relationship between several distance-independent indices (surface
brightness, color, metallicity, and velocity dispersion) the field and
cluster galaxies differed systematically. The sense of these
differences was that field galaxies were bluer, had higher surface
brightness, and were more metal-poor than their field counterparts of
similar velocity dispersion. They proposed that these differences
would follow logically from star-formation histories if the field
ellipticals were typically younger than cluster ellipticals. A
related study was carried out by Guzmàn and coworkers
(Guzmàn 1994
;
Guzmàn & Lucey
1993
;
Guzmàn, Lucey,
& Bower 1993
;
cf.,
Gregg 1992),
who also concluded that metallicity influences the
fundamental plane relations (Section 6.1.2).
Guzmàn (1994)
explicitly argued that this "age effect" induces a significant
difference between
Dn- distances for cluster and field galaxies,
and that with appropriate corrections, the large peculiar velocities
obtained from
Dn-
distances for cluster and field galaxies,
and that with appropriate corrections, the large peculiar velocities
obtained from
Dn- data
(Section 7.1) vanish.
data
(Section 7.1) vanish.
There are, however, good reasons to view the results of the previous
paragraph with considerable caution. The study by
de Carvalho &
Djorgovski (1992)
mixed two data sets, those of
Djorgovski & Davis
(1987)
and of the 7S group
(Faber et al. 1989),
which might well
differ systematically from one another. Indeed, it is primarily the
Djorgovski & Davis
(1987)
data set which manifests a clear
cluster/field offset as measured by the distance-independent indices;
no significant effect is found in the 7S data set. The work of
Guzmàn and coworkers has been questioned on a variety of grounds
(D. Burstein, private communication), in particular the use of an
erroneous metallicity-velocity dispersion correlation and outdated
stellar population models. Finally, it should be noted that the 7S
group tested for metallicity and color dependences of the
Dn- relations and found them to be statistically insignificant
(Lynden-Bell et
al. 1988b).
The 7S group recognized the existence of
a fraction (~ 10-20%) of the total elliptical population in which
stellar population anomalies might be present, but showed that these
objects did not strongly affect their conclusions about the
systematics of the flows
(Burstein et al. 1990).
relations and found them to be statistically insignificant
(Lynden-Bell et
al. 1988b).
The 7S group recognized the existence of
a fraction (~ 10-20%) of the total elliptical population in which
stellar population anomalies might be present, but showed that these
objects did not strongly affect their conclusions about the
systematics of the flows
(Burstein et al. 1990).
Another means of assessing whether measured peculiar velocities could
be due to DI non-universality is to compare the velocity field in a
given region of space obtained from different DIs.
Kolatt & Dekel
(1994)
compared the peculiar velocity fields reconstructed by the
POTENT technique (Section 7.5) from
spiral (TF) and elliptical
(Dn- ) data
separately, and found no statistically meaningful
differences between the two. It is unlikely that zeropoint gradients
would affect TF and
Dn-
) data
separately, and found no statistically meaningful
differences between the two. It is unlikely that zeropoint gradients
would affect TF and
Dn- in
precisely the same way. Another
consistency test derives from a comparison of
Dn-
in
precisely the same way. Another
consistency test derives from a comparison of
Dn- distances with
distances obtained for the same galaxies using the Surface Brightness
Fluctuation (SBF) technique
(Dressler 1994
;
see Section 6.3.1).
This comparison has validated
Dn-
distances with
distances obtained for the same galaxies using the Surface Brightness
Fluctuation (SBF) technique
(Dressler 1994
;
see Section 6.3.1).
This comparison has validated
Dn- peculiar velocity estimates
for ~ 15 ellipticals in the Southern sky. Since the SBF technique is
thought to be highly accurate, and involves measurements entirely
unrelated to
Dn-
peculiar velocity estimates
for ~ 15 ellipticals in the Southern sky. Since the SBF technique is
thought to be highly accurate, and involves measurements entirely
unrelated to
Dn- , these
results represent another encouraging
(albeit preliminary) indication of
Dn-
, these
results represent another encouraging
(albeit preliminary) indication of
Dn- universality.
universality.
In summary, then, there is no compelling evidence at present for
substantial spatial or environmental variations in the TF or
Dn- relations. While there exist some indications that metallicity and/or
age effects enter into the fundamental plane relations for a fraction
of elliptical galaxies, these effects apparently do not influence the
distance estimates obtained from
Dn-
relations. While there exist some indications that metallicity and/or
age effects enter into the fundamental plane relations for a fraction
of elliptical galaxies, these effects apparently do not influence the
distance estimates obtained from
Dn- in a
systematic way. As
more data are acquired in the coming years, using a multiplicity of
DIs, intercomparisons will permit more sensitive tests of DI
universality.
in a
systematic way. As
more data are acquired in the coming years, using a multiplicity of
DIs, intercomparisons will permit more sensitive tests of DI
universality.
6.3. Beyond TF and Dn -
 : A Look to the
Future?
: A Look to the
Future?
While the TF and
Dn- methods have been the workhorses in
peculiar velocity surveys, there a number of other promising distance
indicators likely to play a role in coming years.
methods have been the workhorses in
peculiar velocity surveys, there a number of other promising distance
indicators likely to play a role in coming years.
6.3.1. Surface Brightness Fluctuations
Over the last several years Tonry and collaborators (Tonry & Schneider 1988 ; Tonry, Ahjar, & Luppino 1989, 1990; Tonry & Schechter 1990 ; Tonry 1991) have begun to exploit an old idea first discussed in detail by Baum (1955) : a sufficiently high resolution image of an elliptical galaxy will reveal the discrete nature of the ultimate sources of luminosity - billions of individual stars. A finite number of stars are included in a single pixel of an image; this number is subject to Poisson fluctuations, and therefore so is the pixel intensity. The farther away the galaxy is, the greater is the number of stars per pixel, and the smaller the Poisson fluctuations; thus the fluctuations are a measure of the distance of the galaxy. Tonry measures the surface brightness fluctuation (SBF) which characterizes an image. The mean SBF can in turn be related to the luminosity of the giant branch stars which dominate the light, which depends weakly on metallicity. The technique is applied to ellipticals rather than spirals because the latter are multicomponent, often dusty systems in which the purely Poisson fluctuations cannot easily be isolated.
The uncertainty in SBF distance estimates varies in inverse proportion
with the resolution of the images obtained. For galaxies within ~
3000
km s-1, SBF distances are estimated to have ~ 5% accuracy under
the best observing conditions. Ground-based resolution is limited by
microturbulence in the atmosphere ("seeing"). In collaboration with
Tonry, Dressler (1994)
has undertaken a program to obtain SBF
distances for ellipticals studied with the
Dn- method
using CCD
images acquired at the du Pont Telescope in Chile, where the seeing is
often
method
using CCD
images acquired at the du Pont Telescope in Chile, where the seeing is
often
 1". This program
promises to yield accurate distances
for nearby ellipticals, and may significantly improve our knowledge of
the local peculiar velocity field. Extension of the SBF technique to
distances of ~ 5000 km s-1 and beyond will require either a
dedicated program of space-based imaging, or the use of adaptive
optics technology for enhancing ground-based resolution.
1". This program
promises to yield accurate distances
for nearby ellipticals, and may significantly improve our knowledge of
the local peculiar velocity field. Extension of the SBF technique to
distances of ~ 5000 km s-1 and beyond will require either a
dedicated program of space-based imaging, or the use of adaptive
optics technology for enhancing ground-based resolution.
The DIs discussed thus far apply to ordinary spiral or elliptical
galaxies. There is also a class of extraordinary galaxies, the most
luminous objects in the centers of rich clusters (called "brightest
cluster galaxies" or BCGs), which can be used as DIs. BCGs were
originally of interest because they are easily identified out to
fairly large (z  0.2)
redshifts. As a result, they were
thought to be ideal tools for studying problems such as the linearity
of the Hubble expansion
(Sandage 1972
;
Sandage & Hardy
1973
;
Gunn & Oke 1975
)
(23)
In addition, because they are highly
luminous objects and are unique in their environment, their study is
not subject to the statistical biases associated with sample
incompleteness we discuss in Section 6.4.
0.2)
redshifts. As a result, they were
thought to be ideal tools for studying problems such as the linearity
of the Hubble expansion
(Sandage 1972
;
Sandage & Hardy
1973
;
Gunn & Oke 1975
)
(23)
In addition, because they are highly
luminous objects and are unique in their environment, their study is
not subject to the statistical biases associated with sample
incompleteness we discuss in Section 6.4.
The studies just mentioned considered BCGs as standard candles, i.e., they assumed their luminosities were independent of any other galaxian property. Later, Hoessel (1980) showed that BCG luminosity correlates with the shape of the luminosity profile. Specifically, Hoessel defined a metric luminosity Lm as the total light interior to the metric radius rm = 10 h-1 kpc, and a luminosity shape parameter
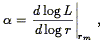
| (162) |
and found a linear correlation between Lm and
 . Recently,
the L-
. Recently,
the L- relation has
been exploited by Lauer & Postman
(1994;
LP), and
Postman & Lauer
(1995)
,
who studied the BCGs in the 119
Abell (1958)
and
Abell, Corwin, &
Olowin (1989)
clusters with redshifts less than 15,000 km s-1. LP found a
quadratic L-
relation has
been exploited by Lauer & Postman
(1994;
LP), and
Postman & Lauer
(1995)
,
who studied the BCGs in the 119
Abell (1958)
and
Abell, Corwin, &
Olowin (1989)
clusters with redshifts less than 15,000 km s-1. LP found a
quadratic L- relation with an equivalent distance error of ~ 16%, comparable to
the TF scatter. The BCG
L-
relation with an equivalent distance error of ~ 16%, comparable to
the TF scatter. The BCG
L- relation is
perhaps the most
promising technique for extending peculiar velocity studies to much
larger scales (z
relation is
perhaps the most
promising technique for extending peculiar velocity studies to much
larger scales (z  0.1) than is currently possible, although it
requires further study to test its universality.
0.1) than is currently possible, although it
requires further study to test its universality.
6.3.3. Possible Methods of Future Peculiar Velocity Work
Two other DIs have recently been the focus of intense observational
work, but thus far in the context of the distance scale (i.e.,
Hubble
constant determination) rather than the velocity field. The first of
these is fitting the planetary nebula luminosity function (PNLF;
Jacoby et al. 1989
;
Ciardullo et al. 1989a,
b;
Jacoby et al. 1990;
Ciardullo, Jacoby,
& Harris 1991).
"Planetary nebulae" are the
luminescent ejectae of dying stars soon to become white dwarfs.
Planetary nebulae may be detected and photometered in nearby (
cz  1500
km s-1) elliptical galaxies using narrow-band
imaging in the light of twice-ionized oxygen at
1500
km s-1) elliptical galaxies using narrow-band
imaging in the light of twice-ionized oxygen at
 = 5007 Å. The PNLF in
this emission line is observed to have a universal form, with a sharp
cutoff at the highest luminosities
(Jacoby 1989
;
Ciardullo et
al. 1989a).
Fitting the observed distribution of planetary nebula
brightnesses to the universal PNLF yields the distance to a galaxy
with ~ 5% accuracy. The PNLF and SBF methods yield consistent
distances for Virgo Cluster galaxies
(Ciardullo, Jacoby,
& Tonry 1993).
At distances much greater than that of Virgo it is quite
difficult to reliably identify even luminous planetary nebulae using
present techniques
(Jacoby et al. 1992).
As a result, the usefulness
of the PNLF method for peculiar velocity work is uncertain.
= 5007 Å. The PNLF in
this emission line is observed to have a universal form, with a sharp
cutoff at the highest luminosities
(Jacoby 1989
;
Ciardullo et
al. 1989a).
Fitting the observed distribution of planetary nebula
brightnesses to the universal PNLF yields the distance to a galaxy
with ~ 5% accuracy. The PNLF and SBF methods yield consistent
distances for Virgo Cluster galaxies
(Ciardullo, Jacoby,
& Tonry 1993).
At distances much greater than that of Virgo it is quite
difficult to reliably identify even luminous planetary nebulae using
present techniques
(Jacoby et al. 1992).
As a result, the usefulness
of the PNLF method for peculiar velocity work is uncertain.
A DI which has been around for some time, but which is currently
undergoing a kind of renaissance, is the mean absolute luminosity of
Type Ia Supernovae (Sne Ia). Of all the DIs discussed here, Sne Ia
have the best-understood physical basis. It is generally agreed that
Sne Ia result from thermonuclear disruption of a carbon-oxygen white
dwarf that has accreted enough mass from a companion star to approach
the Chandrasekhar mass of ~ 1.4
M (e.g.,
Wheeler & Harkness
1990
and references therein). The radioactive decay of
56Ni and
56Co following the explosion power the subsequent
observable light curve. Theoretical models suggest that the mass of
the nickel ejectae is in the range 0.6-0.8
M
(e.g.,
Wheeler & Harkness
1990
and references therein). The radioactive decay of
56Ni and
56Co following the explosion power the subsequent
observable light curve. Theoretical models suggest that the mass of
the nickel ejectae is in the range 0.6-0.8
M (Arnett et al. 1985);
when combined with the observed rise time to maximum light of
~ 17 days, an absolute luminosity of
MB
(Arnett et al. 1985);
when combined with the observed rise time to maximum light of
~ 17 days, an absolute luminosity of
MB  - 19.6
mag is predicted.
- 19.6
mag is predicted.
There has been some controversy over their intrinsic scatter as standard candles. The discovery that the peak luminosity of SN 1a correlates with their rate of decline (Pskovskii 1977 , 1984; Phillips 1993 ; Hamuy et al. 1995 , but see Tammann & Sandage 1995) may tighten up the scatter considerably, to as small as 0.1-0.2 mag (Hamuy et al. 1995 ; Reiss, Press, & Kirshner 1995).
Sne Ia have been used almost exclusively for Hubble constant determination (e.g., Saha et al. 1994 a, b). Indeed, their idiosyncratic nature as DIs - one must wait for a supernova to appear in a galaxy in order to estimate its distance, and their occurrence is both unpredictable and rare - limits their utility for peculiar velocity work. However, they can be used as DIs to extremely large distances with relatively little loss of accuracy (e.g., Perlmutter et al. 1993), and may thus prove useful in extensions of peculiar velocity analyses to large distances.
Type II supernovae, which mark the end-point of the life of a massive star, can also be used as a distance indicator (Schmidt, Kirshner, & Eastman 1992 ; 1994). Spectroscopic observations yield the velocity of the ejecta and the temperature of the outer layers, from which the absolute brightness can be inferred with the use of model atmospheres. Comparison with the apparent brightness yields a distance. This method requires extensive model calculations and detailed observations, and has thus far been applied only to a handful of objects.
6.4. Statistical Bias and Methods of Peculiar Velocity Analysis
With the possible exception of the SBF technique, the DIs used in
peculiar velocity surveys are not very accurate. The TF and
Dn- relations, for example, predict galaxy distances with only ~ 20%
accuracy. In the volume within which we hope to study the peculiar
velocity field in reasonable detail, typical galaxies may lie at
distances of ~ 3000
km s-1. The rms peculiar velocity error for such
a galaxy is thus on the order of 600 km s-1, which also
happens to be
the amplitude of typical peculiar velocities. At interesting
distances, then, we cannot measure with any precision the peculiar
velocity of a single galaxy. Meaningful analyses must use statistical
techniques applied to large samples.
relations, for example, predict galaxy distances with only ~ 20%
accuracy. In the volume within which we hope to study the peculiar
velocity field in reasonable detail, typical galaxies may lie at
distances of ~ 3000
km s-1. The rms peculiar velocity error for such
a galaxy is thus on the order of 600 km s-1, which also
happens to be
the amplitude of typical peculiar velocities. At interesting
distances, then, we cannot measure with any precision the peculiar
velocity of a single galaxy. Meaningful analyses must use statistical
techniques applied to large samples.
At first glance, this might not be considered a major problem. There
are, after all, thousands of galaxies in the local volume for which we
have obtained, or soon hope to obtain, distance indicator data. We
might expect that by virtue of
 N statistics alone the
signal-to-noise ratio of any statistical analysis could be made rather
high. However, this expectation is not realized in practice. The
analysis of DI data is instead subject to statistical bias effects;
these effects result in random errors dropping more slowly than
1/
N statistics alone the
signal-to-noise ratio of any statistical analysis could be made rather
high. However, this expectation is not realized in practice. The
analysis of DI data is instead subject to statistical bias effects;
these effects result in random errors dropping more slowly than
1/ N, and also in the
possibility of large systematic errors
if the biases are not properly corrected for. While there are a
number of bias effects, all originate in a coupling of the DI scatter
with external influences on the makeup and spatial distribution of the
redshift-distance sample. The goal of this section is to explore the
nature and consequences of this coupling in a variety of circumstances.
N, and also in the
possibility of large systematic errors
if the biases are not properly corrected for. While there are a
number of bias effects, all originate in a coupling of the DI scatter
with external influences on the makeup and spatial distribution of the
redshift-distance sample. The goal of this section is to explore the
nature and consequences of this coupling in a variety of circumstances.
A peculiar velocity analysis has, logically if not sequentially, two
steps. The first is calibration of the DI being used. If we
assume for definiteness that it is the TF relation, calibration means
determination of the zeropoint A, slope b, and scatter
 which quantify the
M-
which quantify the
M- relationship (Section 6.1.1).
The second step in the analysis is the inference
(24)
of distances and thus peculiar
velocities for sample objects. Each step is potentially subject to
biases. Those which enter into the calibration phase, if not
corrected for, can lead to erroneous determinations of any or all of
the parameters A, b, or
relationship (Section 6.1.1).
The second step in the analysis is the inference
(24)
of distances and thus peculiar
velocities for sample objects. Each step is potentially subject to
biases. Those which enter into the calibration phase, if not
corrected for, can lead to erroneous determinations of any or all of
the parameters A, b, or
 . This incorrect TF relation
will
produce incorrect distances and peculiar velocities. Even with a
properly calibrated TF relation, however, uncorrected biases in the
distance-inference phase have the same result.
. This incorrect TF relation
will
produce incorrect distances and peculiar velocities. Even with a
properly calibrated TF relation, however, uncorrected biases in the
distance-inference phase have the same result.
The separation of bias effects into "calibration" and "inferred-distance" problems (Willick 1994) is useful in emphasizing the different ways bias can affect peculiar velocity analyses. However, it does not distinguish the root causes of bias. These lie not in the goal but in the underlying assumptions of the analytic approach, as we will clarify in Section 6.4.1. With one set of assumptions, an analysis will be subject to selection bias, which is intimately related (as the name implies) to observational selection criteria such as a flux limit. With the second set of assumptions, Malmquist bias will result. As defined here (but see next paragraph), Malmquist bias is not fundamentally related to a flux limit or any other selection criteria. It occurs because the true distance of a galaxy cannot be estimated from DI information alone, but requires knowledge of the actual line of sight density distribution as well. Selection bias can affect either DI calibration or peculiar velocity measurement - or both, as they often are carried out simultaneously (Section 6.4.3). Malmquist bias typically enters only when a calibrated DI is used to infer peculiar velocities; approaches to DI calibration which are subject to Malmquist bias are rarely used in practice and will not concern us here.
We organize our discussion mainly around the selection/Malmquist dichotomy, but we note that this distinction has rarely been maintained in the existing literature, where much confusion reigns. One source of confusion is the ambiguity surrounding the term "Malmquist bias," which historically has meant several different things. The term originated with the work of Malmquist (1924) , who showed that flux limited samples were subject to a luminosity bias - one which in fact resembles our selection bias more closely than our Malmquist bias. Thus, early discussions of DI bias (Sandage, Tammann, & Yahil 1979 ; Teerikorpi 1984 , 1987; Aaronson et al. 1986) typically refer to bias effects associated with flux limits as "Malmquist biases." However, the distinct biases related to the line of sight galaxy density distribution were also referred to as "Malmquist" effects by Lynden-Bell et al. (1988a) , who were the first to discuss them quantitatively in the extragalactic context. The latter usage has gained widespread acceptance, and it is the one we adopt here. Even so the impression has persisted in some quarters that Malmquist bias thus defined relates to a flux limit. One goal of the discussion to follow is to dispel this and related misperceptions brought about by conflicting uses of this catch-all phrase.
6.4.1. Selection vs. Malmquist Bias - Method I vs. Method II
Because of DI errors, data from a large number of galaxies are needed if the estimated peculiar velocity at a given point r is to be of value. Thus, in devising a method of analysis we must ask the question, "for what particular set of objects should data be averaged (25) to estimate peculiar velocity at position r?". There are two methodologically orthogonal answers to this question:
A method based on the first answer will be subject to selection bias; one based on the second answer will experience Malmquist bias. This holds true whether our goals are DI calibration, peculiar velocity measurement, or both.
It will prove useful to have terms describing methods of peculiar
velocity analysis, in addition to terms describing the types of bias
to which they are subject. When redshift-space information is used as
the a priori indicator of true proximity, we will describe the
analysis as belonging to "Method II." When DI information is used as
the a priori indicator of true proximity, we will describe the
analysis as belonging to "Method I." This terminology was originally
introduced by
Faber & Burstein
(1988)
,
although their usage was
somewhat less general than ours. In Section 6.4.2 and
Section 6.4.3, we will show, using prototypical
examples, why
Method II is subject to selection bias and Method I to Malmquist bias,
and clarify how these biases affect the analysis. Later, in
Section 6.5 we will show how to quantify and correct
for these
biases. We will assume throughout that the DI in question is the TF
relation, but the concepts apply equally to DIs such as
Dn- .
.
6.4.2. Bias in a Cluster Sample
Suppose that a flux-limited Tully-Fisher sample consists of spiral
galaxies thought to belong to an isolated rich cluster. A reasonable
assumption to adopt in analyzing such a sample is that its members all
lie at the same distance. This is an example of a Method II analysis:
redshift-space information - from which we infer cluster
membership - is treated as the a priori indicator of distance;
the TF
information has not entered into the assumption in any way. Let us
further suppose that our goal is to calibrate the TF relation. Using
the common distance assumption we may write the expected apparent
magnitude of a cluster galaxy with velocity width parameter
 as
<m(
as
<m( )>
= A -
b
)>
= A -
b +
µ (see Eq. 152), where
µ = 5logrc is the cluster distance
modulus; for now suppose that
the cluster distance rc, in
km s-1, is independently known. We also
expect that the observed apparent magnitudes will scatter about
<m(
+
µ (see Eq. 152), where
µ = 5logrc is the cluster distance
modulus; for now suppose that
the cluster distance rc, in
km s-1, is independently known. We also
expect that the observed apparent magnitudes will scatter about
<m( )>
with rms dispersion
)>
with rms dispersion  . These
considerations seem to suggest that linear regression of m on
. These
considerations seem to suggest that linear regression of m on
 for the
cluster sample will correctly give the TF slope and zeropoint (after
subtracting the distance modulus), and that the scatter about that fit
will yield
for the
cluster sample will correctly give the TF slope and zeropoint (after
subtracting the distance modulus), and that the scatter about that fit
will yield  .
.
However, because we have made a priori distance assignments
based on
redshift-space information, the above exercise will be subject to
selection bias. How, specifically, does the bias enter in? Let
m denote the
magnitude equivalent of the flux limit.
Fig. 13 illustrates a Monte-Carlo simulation
of a Tully-Fisher sample at a common distance, with a scatter of 0.35
mag, and a magnitude selection at
m
denote the
magnitude equivalent of the flux limit.
Fig. 13 illustrates a Monte-Carlo simulation
of a Tully-Fisher sample at a common distance, with a scatter of 0.35
mag, and a magnitude selection at
m = 16. The
dashed line is the
input TF relation. Consider a subset of sample galaxies with similar
and relatively large velocity width parameters
= 16. The
dashed line is the
input TF relation. Consider a subset of sample galaxies with similar
and relatively large velocity width parameters

 1 = 0.2
such that they are typically much brighter than the flux limit,
i.e., <m(
1 = 0.2
such that they are typically much brighter than the flux limit,
i.e., <m( 1)> <<
m
1)> <<
m . Their
observed apparent magnitudes m will
be distributed uniformly about
<m(
. Their
observed apparent magnitudes m will
be distributed uniformly about
<m( 1)> with rms dispersion
1)> with rms dispersion
 . Now consider a second
subset with relatively small width parameters
. Now consider a second
subset with relatively small width parameters

 2 = -
0.2 such that
<m(
2 = -
0.2 such that
<m( 2)>
2)>
 m
m . They will
exhibit a range of apparent magnitudes
m
. They will
exhibit a range of apparent magnitudes
m  <m(
<m( 2)>. However, none will have
m > <m(
2)>. However, none will have
m > <m( 2)>. Such galaxies exist in the cluster, but are
"missing" from the sample because they are fainter than the
magnitude limit. The mean apparent magnitude of the second subset will
therefore be brighter than
<m(
2)>. Such galaxies exist in the cluster, but are
"missing" from the sample because they are fainter than the
magnitude limit. The mean apparent magnitude of the second subset will
therefore be brighter than
<m( 2)>, as the solid
line in the figure shows. This is one definition of bias: the mean
apparent magnitude does not conform to the TF prediction. A linear fit
to the points which does not take into account the magnitude limit
will be biased; as illustrated by the stars in
Fig. 13: the slope of the fitted line is
flatter (by
2 in this example), and the fitted zeropoint is brighter (by 0.3 mag
in this example) than the true TF relation (the dashed line).
2)>, as the solid
line in the figure shows. This is one definition of bias: the mean
apparent magnitude does not conform to the TF prediction. A linear fit
to the points which does not take into account the magnitude limit
will be biased; as illustrated by the stars in
Fig. 13: the slope of the fitted line is
flatter (by
2 in this example), and the fitted zeropoint is brighter (by 0.3 mag
in this example) than the true TF relation (the dashed line).
Finally, the scatter about the fit will not equal
 : because
the faint part of the magnitude distribution at
: because
the faint part of the magnitude distribution at
 2 is
cut off,
the points cluster more tightly around the mean value. The flat slope,
bright zeropoint, and reduced scatter of the fit are all
characteristic of how selection bias affects DI calibration.
2 is
cut off,
the points cluster more tightly around the mean value. The flat slope,
bright zeropoint, and reduced scatter of the fit are all
characteristic of how selection bias affects DI calibration.
The calibration procedure itself was not, however, responsible for
bias in the above example. Suppose that the TF parameters were known
at the outset, and that instead it was the cluster distance modulus
µ whose value was sought. We could still make the assumption
that the cluster galaxies lie at the same distance. We would then seek to
determine µ by fitting a line of known slope - b to
the TF data.
The intercept of that line would (apparently) be A +
µ. Yet even
though A and b are known, the fitted line would still be
displaced
from the correct (TF-predicted) one. Near the magnitude limit, the
observed apparent magnitudes are still brighter in the mean than
<m( )>.
The derived value of µ will thus be biased small;
when combined with the cluster redshift, this will result in a
too-positive radial peculiar velocity. These effects are,
independently of calibration issues, also characteristic of selection
bias.
)>.
The derived value of µ will thus be biased small;
when combined with the cluster redshift, this will result in a
too-positive radial peculiar velocity. These effects are,
independently of calibration issues, also characteristic of selection
bias.
Central to the Method II analyses just described was the assumption
that the cluster galaxies lie at the same distance. This assumption,
though plausible, is not self-evident; the galaxies might conceivably
be spread out over a range of distances. Following this line of
reasoning we might, if our TF relation were independently calibrated,
neglect redshift space data initially and assign distances directly
from the observables m and
 . These
inferred distances
d are derived by forming a distance modulus
µ(m,
. These
inferred distances
d are derived by forming a distance modulus
µ(m,
 ) = m -
M(
) = m -
M( )
and then taking d =
100.2µ(m,
)
and then taking d =
100.2µ(m, ). Because of DI errors, the
true distance r can differ appreciably from d. Still, a
Method I
analysis of the cluster would assume that only galaxies with similar
values of d - not all galaxies in the sample - may be treated as
equidistant. The redshifts of galaxies with similar values of d
would then be averaged together to obtain a mean value
<cz(d)>, and a corresponding inferred peculiar velocity
u(d )= <cz(d)> - d.
). Because of DI errors, the
true distance r can differ appreciably from d. Still, a
Method I
analysis of the cluster would assume that only galaxies with similar
values of d - not all galaxies in the sample - may be treated as
equidistant. The redshifts of galaxies with similar values of d
would then be averaged together to obtain a mean value
<cz(d)>, and a corresponding inferred peculiar velocity
u(d )= <cz(d)> - d.
Because we have now made a priori distance assignments based on the DI information, this analysis will be subject to Malmquist bias. The specific manifestations of this bias are that d, <cz(d)>, and and u(d ) are not equal to the average true distance, redshift, and radial peculiar velocity, respectively, of the set of objects with inferred distance d. The bias arises because objects with inferred distance d come, with varying probability, from a range of true distances r as a result of DI errors. They are constrained to lie within some vicinity of d, but their true distances are influenced by another factor wholly unrelated to the DI information: where along this line of sight galaxies are intrinsically likely to be found. This is quantified by the number of galaxies per unit distance r2n(r), where n(r) is the galaxy number density. If galaxies were in fact widely distributed along the line of sight (n(r) roughly constant), then because there is more volume at larger distances (the r2 factor), d would underestimate the true distance. If on the other hand the common-distance model had been accurate in the first place, then regardless of the value of d the true distance is the cluster distance rc. Inferred distances d < rc would then necessarily underestimate, and d > rc necessarily overestimate, true distance. None of these considerations relates in any way to the selection criteria which define the sample.
When galaxies scatter from r to d because of DI errors, they
"bring with them" the correct redshifts of their true
positions. That is, DI errors do not affect redshifts, but only the
distances at which they are evaluated and converted to peculiar
velocities. Thus, if
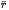 d (say) is the mean
true distance of
galaxies with inferred distance d, the mean redshift of these
galaxies will to first order be <cz(d)> =
d (say) is the mean
true distance of
galaxies with inferred distance d, the mean redshift of these
galaxies will to first order be <cz(d)> =
 d +
ut(
d +
ut( d), where the subscript t signifies
true as opposed to
inferred radial peculiar velocity
(26) .
From this redshift one would infer a peculiar velocity
u(d) =
ut(
d), where the subscript t signifies
true as opposed to
inferred radial peculiar velocity
(26) .
From this redshift one would infer a peculiar velocity
u(d) =
ut( d) +
(
d) +
( d -
d). Thus, the distance bias (d
d -
d). Thus, the distance bias (d

 d) translates
directly into a peculiar
velocity bias. In the case that the galaxies truly constitute a
cluster (i.e.,
d) translates
directly into a peculiar
velocity bias. In the case that the galaxies truly constitute a
cluster (i.e.,
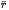 d =
rc for all d), we see that u >
ut when d < rc, and
u < ut when d >
rc. It follows that the inferred radial
peculiar velocity field u(d ) would exhibit a
compressional inflow
into the cluster center, even if there were no real peculiar
velocities. This last effect - spurious peculiar velocities
associated with strong line of sight density gradients, of which a
cluster is the most extreme case - is the most serious consequence of
Malmquist bias. As density gradients generally are not known with
great precision, Malmquist bias can be difficult to correct for
reliably (Section 6.5.2).
d =
rc for all d), we see that u >
ut when d < rc, and
u < ut when d >
rc. It follows that the inferred radial
peculiar velocity field u(d ) would exhibit a
compressional inflow
into the cluster center, even if there were no real peculiar
velocities. This last effect - spurious peculiar velocities
associated with strong line of sight density gradients, of which a
cluster is the most extreme case - is the most serious consequence of
Malmquist bias. As density gradients generally are not known with
great precision, Malmquist bias can be difficult to correct for
reliably (Section 6.5.2).
We used the example of a cluster to distinguish selection and Malmquist bias with maximum clarity. However, peculiar velocity analyses more often involve field galaxy samples. It is therefore important to realize that the two kinds of bias occur, for analogous reasons, in field sample analyses as well. In the cluster example, the Method II approach seemed "natural" in comparison with Method I. With a field sample, the choice of method is not clear cut. We illustrate these issues in what follows.
A Method II analysis of field galaxies usually entails the adoption of
a model of the peculiar velocity field,
v(r; a); the
quantity a is a vector of free parameters which specifies the
model. An important example is a velocity field obtained from
Eq. (150) using redshift survey data, with
 as
the only free parameter. Using the model, one obtains a distance r
for a galaxy of redshift cz as the solution of the equation
as
the only free parameter. Using the model, one obtains a distance r
for a galaxy of redshift cz as the solution of the equation
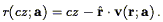
| (163) |
Such an expression of course assumes a unique redshift-distance
mapping, which may not obtain in the vicinity of large mass
concentrations (see Section 5.9), an
issue we will return
to later. From Eq. (163) one can predict the galaxy's
apparent magnitude, given the value of its velocity width parameter
 :
:
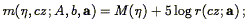
| (164) |
this predicted apparent magnitude depends, as indicated, not only on
the velocity field parameter vector a, but also on the TF
parameters A and b, whose determination might also be part
of the analysis. One can then form a
 2 statistic of
observed minus predicted apparent magnitudes:
2 statistic of
observed minus predicted apparent magnitudes:
| (165) |
(the individual object scatters are usually assumed equal in the simplest implementations of Method II). Minimization of this statistic might then be expected to yield the "best" values of the velocity field parameters a and (if necessary) the TF parameters A and b.
A bit of reflection shows, however, that such an exercise will be
subject to the same bias that affected the first TF analysis of
cluster galaxies discussed in Section 6.4.2. In
particular,
there is again the issue of "missing" galaxies, although in a more
abstract sense than earlier. There is in fact only one galaxy at
redshift czi, direction
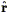 i, and width parameter
i, and width parameter
 i. However, the validity of the
i. However, the validity of the
 2-minimization procedure
requires that this object be representative of the ensemble of all
possible such objects. Because of the flux limit, however, it cannot
be: if the predicted apparent magnitude
m(
2-minimization procedure
requires that this object be representative of the ensemble of all
possible such objects. Because of the flux limit, however, it cannot
be: if the predicted apparent magnitude
m( i,czi; A, b,
a) is
close to or fainter than the flux limit, the fainter members of this
hypothetical ensemble cannot belong to the sample. As a result, the
observed apparent magnitude mi is likely to be
brighter than the predicted value; minimization of
i,czi; A, b,
a) is
close to or fainter than the flux limit, the fainter members of this
hypothetical ensemble cannot belong to the sample. As a result, the
observed apparent magnitude mi is likely to be
brighter than the predicted value; minimization of
 II2(A,
b, a)
consequently does not yield the correct values of the parameters on
which it depends. A Method II analysis of a field sample is thus
affected by selection bias, just as was the earlier one based on the
assumption of equidistant cluster members. We note that although we
have assumed the existence of a model peculiar velocity field, this is
not fundamental to a Method II field sample analysis. For example, if
pure Hubble flow were assumed (v(r;a) vanishes
identically), an exercise identical to that outlined above could be
used just to calibrate the TF relation; its results also would be
affected by selection bias.
II2(A,
b, a)
consequently does not yield the correct values of the parameters on
which it depends. A Method II analysis of a field sample is thus
affected by selection bias, just as was the earlier one based on the
assumption of equidistant cluster members. We note that although we
have assumed the existence of a model peculiar velocity field, this is
not fundamental to a Method II field sample analysis. For example, if
pure Hubble flow were assumed (v(r;a) vanishes
identically), an exercise identical to that outlined above could be
used just to calibrate the TF relation; its results also would be
affected by selection bias.
A Method I analysis of the same sample would proceed differently. To make the comparison as direct as possible, we again suppose that the purpose is to fit a model velocity field v(r; a). Now, however, there is no need to solve Eq. (163) to obtain a distance. Instead we use the inferred distance d as the best indicator of true distance, and thus as the position at which we evaluate the velocity model. Inferred distances are given as described in the Method I cluster analysis (Section 6.4.2), and the TF relation is again assumed to have been independently calibrated (27) . Using the model velocity field we write a predicted redshift for a galaxy with inferred distance d as
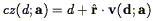
| (166) |
where
d = d  . This in turn motivates
a
. This in turn motivates
a  2 statistic of the form
2 statistic of the form
| (167) |
where  i is a
suitable measure of redshift and distance
errors. Again one might suppose that minimization of this statistic
leads to the best values of the velocity model parameters a.
i is a
suitable measure of redshift and distance
errors. Again one might suppose that minimization of this statistic
leads to the best values of the velocity model parameters a.
However, this naïve approach will lead to biased results. The
validity of the  2
minimization rests on the assumption that
cz(di; a) is an unbiased estimator of
czi when the velocity
model is correct. As discussed in Section 6.4.2,
the object
with inferred distance di can come from a range of
true distances
with varying probability. Let the expected true distance of this
object be
2
minimization rests on the assumption that
cz(di; a) is an unbiased estimator of
czi when the velocity
model is correct. As discussed in Section 6.4.2,
the object
with inferred distance di can come from a range of
true distances
with varying probability. Let the expected true distance of this
object be
 di. Its
observed
redshift then has a corresponding expected value
<czi> =
di. Its
observed
redshift then has a corresponding expected value
<czi> =
 di +
ut(
di +
ut( di),
where as in Section 6.4.2 ut
denotes the true
radial peculiar velocity field and we neglect second order
effects. From this it follows (compare with Eq. 166) that,
even if the velocity model is correct,
<czi>
di),
where as in Section 6.4.2 ut
denotes the true
radial peculiar velocity field and we neglect second order
effects. From this it follows (compare with Eq. 166) that,
even if the velocity model is correct,
<czi>
 cz(di,
a) unless
cz(di,
a) unless
 di =
di. But we know from our discussion of the
Method I cluster analysis (Section 6.4.2) that this
last condition does not hold in general; the relationship between
di =
di. But we know from our discussion of the
Method I cluster analysis (Section 6.4.2) that this
last condition does not hold in general; the relationship between
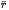 di and
di depends on the details of the underlying density
distribution n(r), which is the essence of Malmquist
bias. Thus
cz(di, a) is a biased measure of
czi, and as a result the
parameters which minimize
di and
di depends on the details of the underlying density
distribution n(r), which is the essence of Malmquist
bias. Thus
cz(di, a) is a biased measure of
czi, and as a result the
parameters which minimize
 I2 yield
an incorrect
velocity field. Again, while we have framed the problem in terms of a
velocity model, Method I includes any analysis in which galaxies with
similar inferred distances are assumed to be physically proximate and,
therefore, to share a peculiar velocity vector. In particular,
nonparametric methods, such as the POTENT reconstruction
(Bertschinger &
Dekel 1989
;
see Section 7.5), which smooth in
inferred-distance space, belong to Method I and suffer from Malmquist
bias.
I2 yield
an incorrect
velocity field. Again, while we have framed the problem in terms of a
velocity model, Method I includes any analysis in which galaxies with
similar inferred distances are assumed to be physically proximate and,
therefore, to share a peculiar velocity vector. In particular,
nonparametric methods, such as the POTENT reconstruction
(Bertschinger &
Dekel 1989
;
see Section 7.5), which smooth in
inferred-distance space, belong to Method I and suffer from Malmquist
bias.
6.4.4. "Inverse" Distance Indicator Relations
There is another basic division between methods of peculiar velocity
analysis, one which has sometimes been subsumed under the Method I/II
dichotomy but in fact is entirely distinct. Until now we have
considered only the "forward" form of DIs, in which the
distance-independent quantity
( in the case of
TF) is thought of
as predicting the distance-dependent quantity (M in the case of
TF). But we can just as easily "turn the relation on its side" and
consider the TF relation as a predictor of velocity width given
absolute magnitude
(28) .
We quantify this prediction as
in the case of
TF) is thought of
as predicting the distance-dependent quantity (M in the case of
TF). But we can just as easily "turn the relation on its side" and
consider the TF relation as a predictor of velocity width given
absolute magnitude
(28) .
We quantify this prediction as
 0(M) (strictly
speaking, the expectation value of
0(M) (strictly
speaking, the expectation value of
 given M),
and call it the "inverse" TF relation. Like its forward counterpart
given M),
and call it the "inverse" TF relation. Like its forward counterpart
 0(M) is
well-described by a linear relation
0(M) is
well-described by a linear relation
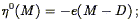
| (168) |
we denote its rms dispersion

 . Because of this
finite scatter
the forward and inverse forms are not mathematically inverse to one
another, i.e.,
e
. Because of this
finite scatter
the forward and inverse forms are not mathematically inverse to one
another, i.e.,
e  b-1
and D
b-1
and D  A. The
forward and inverse
forms of DIs are alternative representations of a single physical
phenomenon; nonetheless, their statistical properties differ markedly.
A. The
forward and inverse
forms of DIs are alternative representations of a single physical
phenomenon; nonetheless, their statistical properties differ markedly.
We illustrate with the following example both this difference in bias
properties, and why the forward/inverse and Method I/II distinctions
have been conflated. Suppose that we wish to carry out a Method II
analysis of the field galaxy sample of
Section 6.4.3 using the
inverse TF relation. In that case we use Eq. (163) to
predict the velocity width parameter
 of an object with
redshift cz and apparent magnitude m as
of an object with
redshift cz and apparent magnitude m as
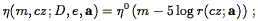
| (169) |
this equation motivates a new
 2 statistic
2 statistic
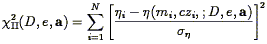
| (170) |
apparently a perfect analogue to its forward counterpart,
Eq. (165). The analogy breaks down, however, when one
considers the bias properties of this inverse statistic. In the
forward case bias arose because the sample galaxy with redshift cz
and velocity width parameter
 was not
representative of the
ensemble of all possible such objects; the presence of a flux limit
meant that the faint end was excluded. In the inverse case the
relevant question is whether the sample galaxy with redshift cz and
apparent magnitude m is representative of all such objects. If we
assume that sample selection is independent of the value of
was not
representative of the
ensemble of all possible such objects; the presence of a flux limit
meant that the faint end was excluded. In the inverse case the
relevant question is whether the sample galaxy with redshift cz and
apparent magnitude m is representative of all such objects. If we
assume that sample selection is independent of the value of
 for
a given m, then the answer to this question is evidently "yes,"
since m must be brighter than the flux limit. There now are no
"missing" galaxies, regardless of how close m is to the flux
limit, and
for
a given m, then the answer to this question is evidently "yes,"
since m must be brighter than the flux limit. There now are no
"missing" galaxies, regardless of how close m is to the flux
limit, and
 (m,
cz; D, e, a) is an unbiased estimator of
(m,
cz; D, e, a) is an unbiased estimator of
 i;
minimization of
i;
minimization of
 II2(D,
e, a) may thus be expected to
yield essentially unbiased values of the free parameters of the model.
II2(D,
e, a) may thus be expected to
yield essentially unbiased values of the free parameters of the model.
This felicitous property of inverse DIs was first noticed by
Schechter (1980)
in a study of the Virgocentric flow field, and was subsequently
exploited to great advantage by
Aaronson et al. (1982b)
and by
Faber & Burstein
(1988) .
These studies enshrined the notion that the
inverse relation was free of selection bias, and also cemented the
association between Method II and the inverse form of DIs. They also,
perhaps because of the catch-all nature of the term "Malmquist," led
to the assertion (e.g.,
Tully 1988)
that inverse DIs are free of
Malmquist bias. None of these conventional notions are accurate. The
above example shows only that an inverse Method II analysis is
unaffected by selection bias when sample selection is independent of
velocity width. The paradigmatic form of sample selection, a
photometric flux limit, which we have used here for illustrative
purposes, is
 -independent.
However, as we discuss below
(Section 6.5.4), in real TF samples selection
criteria are more
complex and may depend, usually weakly, on velocity width. In such
cases, even an inverse Method II analysis will be subject to mild
selection bias. Moreover, there is no inherent connection between
inverse DIs and Method II; the essence of Method II is its a
priori assignment of distances from redshift, after which either
form of the DI can be employed.
-independent.
However, as we discuss below
(Section 6.5.4), in real TF samples selection
criteria are more
complex and may depend, usually weakly, on velocity width. In such
cases, even an inverse Method II analysis will be subject to mild
selection bias. Moreover, there is no inherent connection between
inverse DIs and Method II; the essence of Method II is its a
priori assignment of distances from redshift, after which either
form of the DI can be employed.
Finally, because of the conventional association between Method II and
inverse DIs, it has not generally been recognized that inverse DIs can
be used in Method I analyses. We defer the details to
Section 6.5.5, and note here only that an
inverse inferred
distance is defined (in the case of TF) by the implicit relation
 0(m
- 5logd )=
0(m
- 5logd )=  .
A consequence of this definition, as will
be come clear, is the fact that inverse and forward inferred distances
differ, in general, for a given galaxy. Nonetheless, the fundamental
source of Malmquist bias in forward Method I analyses - that the
likelihood an object will scatter from true distance r to inferred
distance d depends on the density n(r) - is equally
present in an inverse Method I analysis. While the use of forward
vs. inverse affects its details, Malmquist bias inevitably accompanies a
Method I analysis.
.
A consequence of this definition, as will
be come clear, is the fact that inverse and forward inferred distances
differ, in general, for a given galaxy. Nonetheless, the fundamental
source of Malmquist bias in forward Method I analyses - that the
likelihood an object will scatter from true distance r to inferred
distance d depends on the density n(r) - is equally
present in an inverse Method I analysis. While the use of forward
vs. inverse affects its details, Malmquist bias inevitably accompanies a
Method I analysis.
6.4.5. The "Method Matrix" of Peculiar Velocity Analysis
We provide here a succinct summary of the multiple and to some degree overlapping methods of peculiar velocity analysis in the form of a "method matrix." The notion of a matrix derives from the two-dimensional character of the methodology discussed above: peculiar velocity analyses can belong to either Method I or II, and can employ either the forward or inverse form of the relevant DI. The statistical biases present are specific to each case. Table 2 summarizes these ideas; two terms in that table not yet defined, the "Gould effect" and the "Landy-Szalay correction," are discussed in Section 6.5.
| DI type/Method Type | Method I | Method II |
| DI-inferred distance best | Redshift-space data best | |
| indicator of true distance | indicator of true distance | |
| Forward | Malmquist bias | Strong selection bias |
| dist-dep (e.g.mag) predicted | (selection-independent | (depends on observational |
by dist-indep (e.g.
 ) quantity ) quantity
| unless
 "Gould effect") "Gould effect")
| selection criteria) |
| Inverse | Malmquist bias | Weak or no selection bias |
| dist-indep predicted | (selection-dependent, | (bias present if selection |
| by dist-dep quantity | Landy-Szalay possible) | related to dist-indep quantity) |
We have defined Methods I and II and discussed the biases inherent in each; we have not yet indicated why we might choose one over the other. Method I has the advantage of being unburdened by preconceived notions about the relation between redshift and distance. Method II, which requires that we invoke at least some form of redshift-distance relation, is necessarily subject to our theoretical prejudice. Ideally, we would like to know where the galaxies really are, and only later compare these real-space positions with the observed redshifts. The most compelling motivation for this is the possibility of triple-valued zones in dense regions (Fig. 11), where infall patterns along the line-of-sight can result in widely separated galaxies having the same observed redshift. Since Method I considers redshift only after it has placed the galaxies at their DI-inferred distances, this presents no special problem. By contrast, Method II is inherently incapable of dealing with multivaluedness in the redshift-distance mapping. It assumes that redshift uniquely specifies distance and thus presents an overly smooth picture of a velocity field which in reality is rapidly changing. (In Section 8.1.3 we will present a recent variant of Method II which circumvents this particular flaw.)
On the other hand, Method II has the advantage that its statistical aspects are comparatively well-constrained. If we suppose that the velocity field model v(r; a) is not unreasonable, then the dominant errors in the assignment of distances (Eq. 163) come from "noise" in the velocity field, whose rms value in the field appears to be at most ~ 200 km s-1 (Section 5.2.1). The dominant errors in Method I distance assignments come from DI scatter, and are therefore several times larger at interesting distances. Moreover, as we will see more clearly in the following section, we can correct for selection bias in terms of knowable information, namely, observational selection criteria. With inverse DIs we can realistically expect selection bias to be quite small. Correction for Malmquist bias, however, depends on density gradients along the line-of-sight, which are not knowable a priori. We can estimate such gradients from redshift data, but this involves additional assumptions concerning peculiar velocities (needed to map redshift- to real-space density) and smoothing methods. Working with inverse DIs gains us nothing in terms of Malmquist bias. In summary, both Method I and Method II have advantages and disadvantages. As we describe in Chapter 8, both are being used in contemporary peculiar velocity analyses. It should be pointed out, however, that many of the analyses we describe in Chapter 8 were done without proper attention to the biases we describe here, and of the differences between the different entries in the Method Matrix of Table 2. Indeed, there remains much work to be done in exploring all these methods; for example, there is no analysis beyond that of Landy & Szalay (1992) which exploits Method I with an inverse DI.
6.5. Quantifying Statistical Bias
In the last section we presented a qualitative outline of the main
statistical biases affecting distance indicator and peculiar velocity
analysis. In order to correct for these effects, the biases must be
quantified and correction formulae and methods developed. This task
has been the focus of a growing number of workers over the last decade
or so. Sandage and coworkers (e.g.,
Sandage, Tammann, &
Yahil 1979
;
Sandage 1988
;
Federspiel, Sandage,
& Tammann 1994)
have provided
useful, though mainly qualitative, suggestions for treating selection
bias. A quantitative approach to the subject was pioneered by
Teerikorpi, Bottinelli, and collaborators (e.g.,
Teerikorpi 1984
,
1987;
Bottinelli et al. 1986),
and extended by Willick
(1991,
1994).
Malmquist bias (in the DI context) was first treated in detail by
Lynden-Bell et
al. (1988a)
;
this work has been followed up and extended by Willick
(1991,
1995),
Landy & Szalay
(1992)
,
and Gould (1993) .
The bias properties of inverse DIs have been studied by
Schechter (1980)
,
Aaronson et al. (1982b)
,
Faber & Burstein
(1988)
,
Tully (1988)
,
Han (1991)
,
Roth (1993)
,
Willick (1994,
1995), and
Triay,
Lachièze-Rey, & Rauzy (1994) .
We will use the formalism developed by
Willick (1991,
1994,
1995)
who has advocated a
comprehensive approach to the problem. We assume in what follows that
the distance indicator in question is the TF relation, but the
discussion is readily modified to treat comparable DIs such as
Dn- .
.
The material discussed in this section remains controversial, and the formal mathematical approach we have adopted has not been accepted by all of the workers in the field. For example, Mathewson & Ford (1994) have argued that approaches like ours require idealized assumptions about sample selection that are invalid for realistic data sets. They instead separate their sample into "control" and "target" regions, using the former to calibrate the biases in the latter. We believe, however, that such qualitative or semiquantitative approaches are subject to their own caveats (are the control and target regions the same in their bias properties?), and run the risk of obscuring rather than illuminating the principal issues. Unlike much of the rest of the review, we have not attempted here to summarize all the analyses extant in the literature, but rather aim to give a comprehensive coverage of our own approach. This section can be skipped on a first reading.
6.5.1. Forward DIs: Selection Bias
We consider first the formalism appropriate to the forward relation;
the inverse relation is treated in Section 6.5.4. A
starting
point in the quantification of bias is the empirical fact that it is
the TF observables, and not the inferred distances, which
exhibit a roughly Gaussian distribution (e.g.,
Willick et al. 1995c).
Thus, the apparent magnitude of a galaxy with width parameter
 and true distance r is normally distributed about a mean value
M(
and true distance r is normally distributed about a mean value
M( ) + 5log
r with rms dispersion
) + 5log
r with rms dispersion
 , when selection
effects may be neglected. We combine this Gaussian distribution with
the a priori distributions of galaxy distances and width
parameters,
and with a function describing sample selection probability, to obtain
the joint probability distribution of the observables (m,
, when selection
effects may be neglected. We combine this Gaussian distribution with
the a priori distributions of galaxy distances and width
parameters,
and with a function describing sample selection probability, to obtain
the joint probability distribution of the observables (m,
 ) and
the true distance r for a galaxy:
) and
the true distance r for a galaxy:
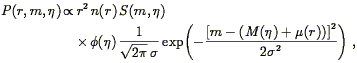
| (171) |
where µ(r) = 5log r,
 (
( ) is the
) is the
 -distribution
function (similar to the luminosity function), and n(r) is the
galaxy number density along the line of sight in question. The
quantity S(m,
-distribution
function (similar to the luminosity function), and n(r) is the
galaxy number density along the line of sight in question. The
quantity S(m,
 ) is the
sample selection function, defined
as the probability an object with observables (m,
) is the
sample selection function, defined
as the probability an object with observables (m,
 ) will be
included in the sample irrespective of other considerations. Note that
we express the selection function here in terms of the observables,
rather than in terms of distance as we did in redshift survey analyses
(Section 3.4). An idealized form of
S(m,
) will be
included in the sample irrespective of other considerations. Note that
we express the selection function here in terms of the observables,
rather than in terms of distance as we did in redshift survey analyses
(Section 3.4). An idealized form of
S(m,  )
describes a sample with a strict magnitude limit,
)
describes a sample with a strict magnitude limit,
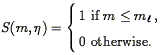
| (172) |
Selection and Malmquist bias effects are each implicit in Eq. (171). Which of the two comes into play depends, as already noted, on the assumptions underlying the method of data analysis; these assumptions determine which of several conditional probability distributions derivable from Eq. (171) are used. We first discuss selection bias; in Section 6.5.2 we discuss Malmquist bias.
We know from Section 6.4.1 that selection biases
arise in Method
II analyses, in which we take redshift-space information as the
a priori distance indicator, either through the assumption of a
common distance for cluster galaxies, or via a redshift-real space
mapping such as Eq. (163). To the extent this mapping is a
good one, we are in effect taking the true distance as
"known" - dependent, perhaps, on model free parameters, but entirely
independent of the TF observables.
(29)
In mathematical terms, this is equivalent to using
probability distributions which are conditioned on the value of the
true distance r. In the forward TF case, the relevant distribution
is
P(m| ,
r), which is readily derived from the joint probability
distribution Eq. 171:
,
r), which is readily derived from the joint probability
distribution Eq. 171:
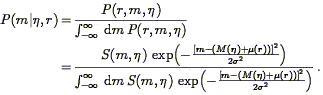
| (173) |
Eq. (173) is the mathematical basis of a forward Method II analysis. The distance r would be replaced by a redshift-space prediction, such as Eq. (163), in an actual implementation of Method II.
If sample selection were independent of apparent magnitude,
S(m,  )
would drop out and Eq. (173) would reduce
to the familiar normal distribution centered on the naïve expected
apparent magnitude
M(
)
would drop out and Eq. (173) would reduce
to the familiar normal distribution centered on the naïve expected
apparent magnitude
M( ) +
µ(r). This is the condition that a
simple
) +
µ(r). This is the condition that a
simple  2
minimization, such as that suggested by
Eq. (165), be valid for determining values of any unknown
model parameters. In a real study, however, sample selection almost
always depends on apparent magnitude, although the dependence is
generally indirect, as we explain below. For simplicity, we first
suppose that in fact a strict magnitude limit, Eq. (172),
applies. In that case Eq. (173) obviously does not
reduce to a normal distribution centered on
M(
2
minimization, such as that suggested by
Eq. (165), be valid for determining values of any unknown
model parameters. In a real study, however, sample selection almost
always depends on apparent magnitude, although the dependence is
generally indirect, as we explain below. For simplicity, we first
suppose that in fact a strict magnitude limit, Eq. (172),
applies. In that case Eq. (173) obviously does not
reduce to a normal distribution centered on
M( ) +
µ(r). It is,
rather, straightforward to show that the expected apparent magnitude
is given by
) +
µ(r). It is,
rather, straightforward to show that the expected apparent magnitude
is given by
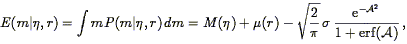
| (174) |
where
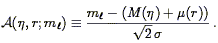
| (175) |
The last term on the right hand side of Eq. (174) is the
apparent magnitude bias, the difference between actual and
naïve expectation values. Its significance is determined by the
parameter
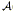 (
( ,
r;m
,
r;m ), a
dimensionless measure of how
"close" the object is expected to be to the magnitude limit. For
), a
dimensionless measure of how
"close" the object is expected to be to the magnitude limit. For
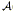
 1, the bias is small;
in that case few galaxies are
"missing" due to the magnitude limit. But for
1, the bias is small;
in that case few galaxies are
"missing" due to the magnitude limit. But for
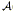
 0, the
hypothetical ensemble of galaxies of given
0, the
hypothetical ensemble of galaxies of given
 and r is
strongly
truncated by the magnitude limit, and the bias is comparable to or
greater than the TF scatter. Note that the sense of the bias is that
objects are typically brighter than the naïve TF prediction,
as we saw in Section 6.4.1.
In any magnitude-limited sample, a large fraction of the objects are
likely to be near the magnitude limit. Hence, the bias represented by
Eq. (174) is a problematic issue in most Method II
analyses (30) .
and r is
strongly
truncated by the magnitude limit, and the bias is comparable to or
greater than the TF scatter. Note that the sense of the bias is that
objects are typically brighter than the naïve TF prediction,
as we saw in Section 6.4.1.
In any magnitude-limited sample, a large fraction of the objects are
likely to be near the magnitude limit. Hence, the bias represented by
Eq. (174) is a problematic issue in most Method II
analyses (30) .
In real samples, the situation is more complicated. TF and
Dn- samples are drawn from catalogs culled from photographic plate
material. Such catalogs (see Section 3.1)
typically
list galaxy apparent magnitudes and/or angular diameters on a
measurement system different from that used by the DI. The catalog
might give, for example, blue-bandpass photographic magnitudes
(mB), while the TF study uses I band CCD magnitudes
(mI).
Candidates for the TF sample might be required to satisfy
mB
samples are drawn from catalogs culled from photographic plate
material. Such catalogs (see Section 3.1)
typically
list galaxy apparent magnitudes and/or angular diameters on a
measurement system different from that used by the DI. The catalog
might give, for example, blue-bandpass photographic magnitudes
(mB), while the TF study uses I band CCD magnitudes
(mI).
Candidates for the TF sample might be required to satisfy
mB  m
m , but once
thus selected, the allowed values of mI are
unrestricted (the CCD photometry is far deeper than the catalog).
Nonetheless, it is clear that the distribution of I band magnitudes
must affected by this selection procedure, as mI is
sure to be
correlated with mB. Analogous statements hold if the
sample is limited by catalog diameter rather than magnitude.
, but once
thus selected, the allowed values of mI are
unrestricted (the CCD photometry is far deeper than the catalog).
Nonetheless, it is clear that the distribution of I band magnitudes
must affected by this selection procedure, as mI is
sure to be
correlated with mB. Analogous statements hold if the
sample is limited by catalog diameter rather than magnitude.
Willick (1994)
has shown how this problem of an "indirect" magnitude
limit may be dealt with in several practical situations. Let us refer
to the quantity determining sample inclusion as
 , which might be
a photographic magnitude or logarithmic diameter, and assume it is
required to satisfy
, which might be
a photographic magnitude or logarithmic diameter, and assume it is
required to satisfy 


 . The selection probability for
an object with TF observables (m,
. The selection probability for
an object with TF observables (m,
 ) is then given by
) is then given by
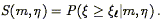
| (176) |
The quantity on the right hand side may be determined by first
assuming that
P( |
m,
|
m, ) is a
Gaussian centered on a mean relation
) is a
Gaussian centered on a mean relation
 (m,
(m,
 ) and with rms
dispersion
) and with rms
dispersion

 . Both may be
determined empirically from the data;
Willick et al. (1995a,
b) have
shown that
. Both may be
determined empirically from the data;
Willick et al. (1995a,
b) have
shown that  (m,
(m,
 ) is well modeled
as linear in m and
) is well modeled
as linear in m and
 when
when  is a
photographic apparent magnitude or logarithmic
diameter. The resulting Gaussian probability distribution is then
integrated over the allowed values of
is a
photographic apparent magnitude or logarithmic
diameter. The resulting Gaussian probability distribution is then
integrated over the allowed values of
 :
:
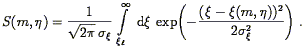
| (177) |
This selection function may be substituted into Eq. (173), and the expected apparent magnitude, and thus the bias, may then be obtained in the usual way. The results, given by Willick (1994) , are complicated and need not be reproduced here. We note only that, as in the case of a strict magnitude limit, the bias again depends on a "limit closeness parameter," given in the present case by
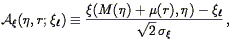
| (178) |
and is also proportional to a "coupling" parameter



 /
/

 , which measures
the tightness of the TF relation relative to that of the
, which measures
the tightness of the TF relation relative to that of the
 -(m,
-(m,
 ) correlation. In
particular, when the latter correlation is weak, the bias is small,
since selection criteria only weakly constrain the apparent magnitude
used in the TF analysis. In most real samples, however, the
) correlation. In
particular, when the latter correlation is weak, the bias is small,
since selection criteria only weakly constrain the apparent magnitude
used in the TF analysis. In most real samples, however, the
 -(m,
-(m,
 ) correlation is
strong enough that even the bias due
to "indirect" limits is significant. Another feature of an indirect
limit is that, if
) correlation is
strong enough that even the bias due
to "indirect" limits is significant. Another feature of an indirect
limit is that, if  is significantly correlated with
is significantly correlated with
 as
well as with m, sample selection probability is
as
well as with m, sample selection probability is
 -dependent;
the consequences of this are discussed in
Section 6.5.4.
-dependent;
the consequences of this are discussed in
Section 6.5.4.
The formulae given by
Willick (1994)
for the magnitude and dispersion
biases allow one to correct for selection bias. The basic idea is to
iterate least-squares fits of the underlying model, using the
parameter estimates from one iteration to correct the next for bias.
"Corrected" apparent magnitudes m(c), defined as the
observed
magnitudes plus the computed bias, are used in the iterated fits.
This procedure typically produces convergent parameter values in ~
10 iterations, and has been used by
Willick et al. (1995a,
b) to
calibrate TF relations for recent peculiar velocity analyses. An
alternative to iteration is direct likelihood maximization, using
individual object probability functions
P(m |
 , r) given by
Eq. (173).
, r) given by
Eq. (173).
In Fig. 14 we illustrate the effects of
selection bias
on both DI calibration and distance determination using numerically
simulated data. Each simulated data set consisted of two clusters
with 25 galaxies each. The distance to the first cluster was fixed at
r1 = 1500 km s-1, which was
assumed known to the "observer." The
second cluster was stepped out in distance, as shown on the horizontal
axis; its distance r2 was assumed unknown to the
"observer."
Determination of its distance modulus µ2 was
assumed to be one
goal of the analysis; the other was determination of the TF parameters
A and b. The simulated data obey a TF relation with slope
b = 7.5 and scatter
 = 0.35 mag; sample
selection was imposed by requiring galaxies to have photographic diameters
= 0.35 mag; sample
selection was imposed by requiring galaxies to have photographic diameters
 1'. These
diameters were generated from the TF observables (m,
1'. These
diameters were generated from the TF observables (m,
 ) using
empirical relations from real data sets
(Willick et al. 1995a
b).
) using
empirical relations from real data sets
(Willick et al. 1995a
b).
For each simulated data set the TF parameters A and b, and the
distance modulus of the second cluster µ2, were
solved for using
standard least-squares techniques. An rms scatter about the fit was
computed separately in each cluster. The results of these
least-squares fits are shown in the left-hand panels of
Fig. 14. As the second cluster moves farther
away, so
that an ever-larger fraction of its member galaxies are near the
diameter limit, the bias increases: the top and middle panels show
that the fitted slope and rms scatter (in the second cluster) become
progressively smaller as the second cluster moves farther away. (The
fitted slope levels out at large distances because it is strongly
constrained by data in the first cluster, which is close enough to be
nearly unbiased.) The bottom panel shows the error in the
least-squares determination of the distance modulus of the second
cluster,
 µ2 =
µ2 - 5logr2. This error is in
the sense
that the distance is underestimated, and grows fractionally
worse with increasing distance. The right hand panel of
Fig. 14 show the same quantities following
application
of the iterative bias correction scheme discussed above. As can be
seen, the iterative method yields unbiased final values of the slope,
scatter, and distance of the second cluster.
µ2 =
µ2 - 5logr2. This error is in
the sense
that the distance is underestimated, and grows fractionally
worse with increasing distance. The right hand panel of
Fig. 14 show the same quantities following
application
of the iterative bias correction scheme discussed above. As can be
seen, the iterative method yields unbiased final values of the slope,
scatter, and distance of the second cluster.
6.5.2. Forward DIs: Malmquist Bias
Malmquist bias arises in Method I analyses, in which we first assign
distances directly from the DI, and consider redshift information only
afterward. As discussed above, the large scatter of DIs such as TF or
Dn- guarantees that objects with inferred distance d come,
with varying probability, from a wide range of true distances. The
probability distribution of true distance r given inferred distance
d is thus the mathematical basis for treating Malmquist bias.
guarantees that objects with inferred distance d come,
with varying probability, from a wide range of true distances. The
probability distribution of true distance r given inferred distance
d is thus the mathematical basis for treating Malmquist bias.
The simplest way to arrive at P(r| d ) is first to consider P(r, µ(d)), which we obtain from Eq. (171) as follows:
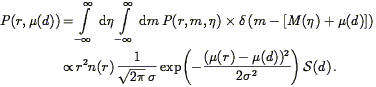
| (179) |
In Eq. (179)  is the
Dirac delta function, and we have defined
is the
Dirac delta function, and we have defined
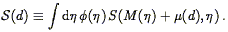
| (180) |
Converting to natural logarithms we derive
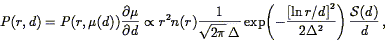
| (181) |
where 
 (ln 10 / 5)
(ln 10 / 5) 
 0.46
0.46
 is a measure of the
fractional distance uncertainty of the DI. The desired
conditional probability is then given by
is a measure of the
fractional distance uncertainty of the DI. The desired
conditional probability is then given by
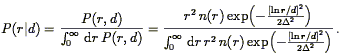
| (182) |
We see that S(m,
 ) has dropped out
entirely in Eq. (182);
selection bias does not play a role in forward Method I analyses. This
may appear odd at first glance; one would think that because selection
depletes the sample more at r > d than at r <
d, it must
affect the ratio of near and far objects at inferred distance d.
The reason it does not may be understood heuristically as
follows. Objects at r < d must be intrinsically fainter
than expected for their velocity width (M >
M(
) has dropped out
entirely in Eq. (182);
selection bias does not play a role in forward Method I analyses. This
may appear odd at first glance; one would think that because selection
depletes the sample more at r > d than at r <
d, it must
affect the ratio of near and far objects at inferred distance d.
The reason it does not may be understood heuristically as
follows. Objects at r < d must be intrinsically fainter
than expected for their velocity width (M >
M( )) in
order to scatter out to d; objects at r >
d must be brighter than expected (M <
M(
)) in
order to scatter out to d; objects at r >
d must be brighter than expected (M <
M( )) in
order to scatter in to d. Thus,
although the sample as a whole is progressively depleted with
distance, the set of objects with inferred distance d is atypical:
its closer members are unusually faint, and its more distant members
are unusually bright. This discrepancy exactly balances the overall
decrease in sampling density with distance. It is important to note,
however, that this argument is specific to the forward form of the DI
(we show how inverse DIs differ in this respect in
Section 6.5.5) and to the absence of an explicit
distance-dependence in the sample selection function (in
Section 6.5.3 we demonstrate how such a dependence
might arise).
)) in
order to scatter in to d. Thus,
although the sample as a whole is progressively depleted with
distance, the set of objects with inferred distance d is atypical:
its closer members are unusually faint, and its more distant members
are unusually bright. This discrepancy exactly balances the overall
decrease in sampling density with distance. It is important to note,
however, that this argument is specific to the forward form of the DI
(we show how inverse DIs differ in this respect in
Section 6.5.5) and to the absence of an explicit
distance-dependence in the sample selection function (in
Section 6.5.3 we demonstrate how such a dependence
might arise).
Although independent of observational selection, forward Malmquist bias is nonetheless a complicated effect. It is best illustrated by considering the expectation value of r given d :
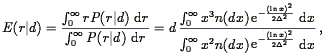
| (183) |
where x = r / d. Eq. (183) shows that, in general
E(r | d)
 d; that is, the inferred
distance is biased. It also
shows that Malmquist bias depends on the number density of galaxies
all along the line of sight, and thus is a nonlocal effect.
d; that is, the inferred
distance is biased. It also
shows that Malmquist bias depends on the number density of galaxies
all along the line of sight, and thus is a nonlocal effect.
The simplest (though usually unrealistic) example of Malmquist bias
occurs when density gradients are negligible on the scale of distance
errors (i.e., n' / n <<
(d )-1). In
that case, the density term drops out of Eq. (183). The integrals
are then easily evaluated with the result
)-1). In
that case, the density term drops out of Eq. (183). The integrals
are then easily evaluated with the result
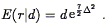
| (184) |
Thus even in the case of uniform density
E(r| d)  d. This effect,
uniform density Malmquist bias, is due to the increasing volume
element at larger distances: there are more galaxies at r >
d than at r < d, and thus
E(r| d ) > d; for a typical distance
indicator (
d. This effect,
uniform density Malmquist bias, is due to the increasing volume
element at larger distances: there are more galaxies at r >
d than at r < d, and thus
E(r| d ) > d; for a typical distance
indicator ( ~ 0.2) it is a ~
15% effect. More
generally, density gradients cannot be neglected, and can either
reinforce or work against the volume effect. This is most easily seen
in the approximation that n(r) is slowly varying on the
scale of DI
errors. Expanding n(r) to first order in Eq. (183)
then yields
~ 0.2) it is a ~
15% effect. More
generally, density gradients cannot be neglected, and can either
reinforce or work against the volume effect. This is most easily seen
in the approximation that n(r) is slowly varying on the
scale of DI
errors. Expanding n(r) to first order in Eq. (183)
then yields
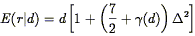
| (185) |
where
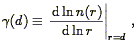
| (186) |
where we have further assumed
 2 << 1.
Eqs. (184) and (185) were first
derived in the extragalactic context by Lynden-Bell et al.
(1988a;
cf., Malmquist 1920).
2 << 1.
Eqs. (184) and (185) were first
derived in the extragalactic context by Lynden-Bell et al.
(1988a;
cf., Malmquist 1920).
The slowly-varying approximation Eq. (185) illustrates
in a general way the effect of density gradients on the statistical
properties of inferred distances. This effect is also known as
inhomogeneous Malmquist bias or IHM. When
 (d ) > 0, IHM
reinforces the uniform density bias; when
(d ) > 0, IHM
reinforces the uniform density bias; when
 (d ) < 0 it works
against it. While the essence of IHM is shown by the slowly-varying
density approximation, Eq. (185) is in fact a rather
poor approximation to the true IHM for the density fields seen in the
real universe (see below). A proper calculation of IHM requires the
full numerical integration indicated by Eq. (183).
(d ) < 0 it works
against it. While the essence of IHM is shown by the slowly-varying
density approximation, Eq. (185) is in fact a rather
poor approximation to the true IHM for the density fields seen in the
real universe (see below). A proper calculation of IHM requires the
full numerical integration indicated by Eq. (183).
These points are illustrated using simulated data in
Fig. 15, which shows the Malmquist bias
associated with
a very strong density perturbation. Galaxies were simulated along a
line of sight in which the density is given by
n0 + np(r), where
np(r) is a Gaussian perturbation centered at 5000
km s-1, with full width ~ 1200
km s-1 and maximum overdensity
 max = 25.
Galaxies were assumed to be moving with Hubble flow; there are no true
peculiar velocities in this simulation. The number of galaxies per
unit true distance along the line of sight is shown in the upper
panel; the effect of the density peak on the distribution is clear.
The simulated galaxies were required to have diameters
max = 25.
Galaxies were assumed to be moving with Hubble flow; there are no true
peculiar velocities in this simulation. The number of galaxies per
unit true distance along the line of sight is shown in the upper
panel; the effect of the density peak on the distribution is clear.
The simulated galaxies were required to have diameters
 1.2',
although this diameter limit does not affect the character of
Malmquist bias, for reasons described above. The simulated galaxies
obey a TF relation with scatter
1.2',
although this diameter limit does not affect the character of
Malmquist bias, for reasons described above. The simulated galaxies
obey a TF relation with scatter
 = 0.35 mag; the "observer" of
the simulation assigned inferred distances d with a properly
calibrated TF relation. In the lower panel the galaxies have been
binned according to the values of their inferred distances. The
average true distances of the galaxies in each bin are plotted as open
squares.
= 0.35 mag; the "observer" of
the simulation assigned inferred distances d with a properly
calibrated TF relation. In the lower panel the galaxies have been
binned according to the values of their inferred distances. The
average true distances of the galaxies in each bin are plotted as open
squares.
Nowhere do the simulated data follow the Hubble line. Very far from
the density peak (d
 2500 km
s-1 and
d
2500 km
s-1 and
d 7500
km s-1) the
simulated data follow the uniform density Malmquist bias prediction
Eq. (184). However, within ~ 2000
km s-1 of the peak, the
data depart strongly from the uniform density prediction; this is the
IHM effect. The sense is that in the foreground of the peak distances
are underestimated (the squares lie above the long dashed line) and in
the background they are overestimated. The amplitude of these effects
is 500-1000
km s-1. The short dashed line is the prediction of the
slowly varying approximation Eq. (185), using the exact
density gradient. It is apparent that this approximation is extremely
poor; this is because the density varies rapidly on the scale of
distance errors. The heavy solid line is obtained from the exact
formula Eq. (183) by numerical integration of the
true density field, and correctly predicts the bias at all distances.
7500
km s-1) the
simulated data follow the uniform density Malmquist bias prediction
Eq. (184). However, within ~ 2000
km s-1 of the peak, the
data depart strongly from the uniform density prediction; this is the
IHM effect. The sense is that in the foreground of the peak distances
are underestimated (the squares lie above the long dashed line) and in
the background they are overestimated. The amplitude of these effects
is 500-1000
km s-1. The short dashed line is the prediction of the
slowly varying approximation Eq. (185), using the exact
density gradient. It is apparent that this approximation is extremely
poor; this is because the density varies rapidly on the scale of
distance errors. The heavy solid line is obtained from the exact
formula Eq. (183) by numerical integration of the
true density field, and correctly predicts the bias at all distances.
Fig. 15 gives further insight into an issue
touched upon
in Section 6.4.2, namely, why IHM can lead to spurious
peculiar velocities. Suppose that the galaxies depicted in the figure
followed the Hubble flow. Their redshift vs. inferred distance
diagram would then closely resemble the lower panel. The "S-wave"
seen in the figure - measured with respect to the uniform density
prediction - would be interpreted as peculiar velocities if IHM were
neglected. In particular, motions of many hundreds of
km s-1 toward the
density peak would be seen in both the foreground and the
background. Such motions are what is expected from gravitational
instability, but in this example they are merely an artifact of
Malmquist bias. More generally, if gravitational instability is
correct, there are real motions but IHM will cause the observed
motions to be larger. This bias mimics the effect of having more
mass in the density enhancement than actually exists. It follows
that, if not properly accounted for, IHM will result in an
overestimate of  (e.g.,
Eq. 149).
(e.g.,
Eq. 149).
6.5.3. Distance-Dependent Selection Functions: The "Gould Effect"
An important feature of the Malmquist bias equations in
Section 6.5.2 was their independence of observational
selection. This greatly simplifies their application in peculiar
velocity analyses; in particular, it makes the uniform density
correction trivial. However, as was first pointed out by
Gould (1993)
, under certain circumstances this desirable attribute of
Malmquist bias might break down. The origin of this effect is best
understood in terms of the selection function, which we have assumed
to depend explicitly only on the observables (m,
 ), not on
distance. As a result, in the steps leading from Eq. (179)
to Eq. (182) S(m,
), not on
distance. As a result, in the steps leading from Eq. (179)
to Eq. (182) S(m,
 ) naturally
cancelled out. Had the
selection function actually been of the form
S(m,
) naturally
cancelled out. Had the
selection function actually been of the form
S(m, ,
r), it would
not have dropped out, and the result would have been a
selection-dependent equation for Malmquist bias.
,
r), it would
not have dropped out, and the result would have been a
selection-dependent equation for Malmquist bias.
To see how distance-dependent selection might arise, suppose that
selection is based on a blue apparent magnitude which must satisfy
mB  m
m , while the
TF analysis involves a distinct magnitude
m. Now, instead of empirically relating mB to
the TF observables and deriving S(m,
, while the
TF analysis involves a distinct magnitude
m. Now, instead of empirically relating mB to
the TF observables and deriving S(m,
 ) according to
Eq. (176), let us consider the TF relation
MB(
) according to
Eq. (176), let us consider the TF relation
MB( ) satisfied by the absolute
magnitude corresponding to mB. We can then relate the
probability that
mB
) satisfied by the absolute
magnitude corresponding to mB. We can then relate the
probability that
mB  m
m , for a
galaxy of width parameter
, for a
galaxy of width parameter
 and
distance r, to a probability involving the absolute magnitude
MB:
and
distance r, to a probability involving the absolute magnitude
MB:
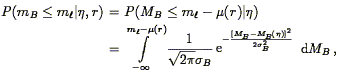
| (187) |
where we have assumed a normally distributed blue TF relation with
scatter  B.
Eq. (187) is apparently nothing but
the sample selection function as we have defined it. However, it is
independent of the TF magnitude m, and explicitly dependent on
r:
rather than writing it S(m,
B.
Eq. (187) is apparently nothing but
the sample selection function as we have defined it. However, it is
independent of the TF magnitude m, and explicitly dependent on
r:
rather than writing it S(m,
 ) we must write it
S(
) we must write it
S( , r).
, r).
How can this derivation be reconciled with
Eq. (176), whose premises appear equally valid but
which yields a qualitatively different result? The answer is quite
subtle, and we refer the reader to
Willick (1995)
for a detailed explanation. There it is shown that Eq. (176) is
valid to the extent that the residuals of the TF relations
MB( )
and M(
)
and M( ) are
strongly correlated, as is normally the case.
Eq. (187) is valid in the opposite limit of uncorrelated
residuals. A rigorous derivation of sample selection must take this
effect into account; the general result is a selection function
S(m,
) are
strongly correlated, as is normally the case.
Eq. (187) is valid in the opposite limit of uncorrelated
residuals. A rigorous derivation of sample selection must take this
effect into account; the general result is a selection function
S(m, ,
r), with the strength of the r-dependence inversely
related to the degree of correlation between the two TF relations.
,
r), with the strength of the r-dependence inversely
related to the degree of correlation between the two TF relations.
There are two methods to determine whether the Gould effect is present
is real samples. The first is to directly examine correlations
between the
MB( ) and
M(
) and
M( ) TF
residuals. The second is to
test whether mB is statistically best described as a
function of
m and
) TF
residuals. The second is to
test whether mB is statistically best described as a
function of
m and  , of
, of
 and r, or
of all three. In the first of
the three cases, there is no Gould effect; otherwise it is present at
some level.
Willick et al. (1995a,
b)
used the second test (with r
modeled by redshift) to show that the effect is significant for
samples selected on the ESO angular diameter (e.g.,
Mathewson et
al. 1992b).
Peculiar velocity analyses using such samples (e.g.,
Hudson et al. 1995)
rely heavily on redshift-space grouping to minimize the effect.
and r, or
of all three. In the first of
the three cases, there is no Gould effect; otherwise it is present at
some level.
Willick et al. (1995a,
b)
used the second test (with r
modeled by redshift) to show that the effect is significant for
samples selected on the ESO angular diameter (e.g.,
Mathewson et
al. 1992b).
Peculiar velocity analyses using such samples (e.g.,
Hudson et al. 1995)
rely heavily on redshift-space grouping to minimize the effect.
6.5.4. Inverse DIs: Selection Bias
A formalism quite analogous to that developed above may be presented
for inverse DIs; we assume, as usual, that the DI in question is TF.
The central element of this formalism is the Gaussian distribution of
observed width parameters about the expectation value
 0(m
- µ(r)) when selection effects are neglected. Adding in
the remaining elements we arrive at the joint distribution of m,
0(m
- µ(r)) when selection effects are neglected. Adding in
the remaining elements we arrive at the joint distribution of m,
 ,
and r written in terms of the inverse TF relation:
,
and r written in terms of the inverse TF relation:
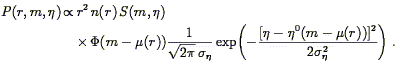
| (188) |
We note that, in contrast to its forward analogue
Eq. (171), this equation involves the luminosity
function  (M).
(M).
Both selection and Malmquist bias are implicit in
Eq. (188). As before the two are distinguished by the
assumptions of data analysis. In a Method II analysis we (implicitly)
condition on the true distance (see
Section 6.5.1). The
probability distribution which underlies such an analysis is thus
P( |
m, r), obtained from Eq. (188) according to
|
m, r), obtained from Eq. (188) according to
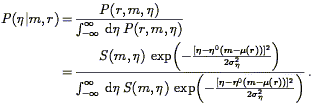
| (189) |
This equation is the inverse counterpart of Eq. (173).
In the forward case the condition for selection bias to vanish was
that S(m,
 ) be independent
of m, which is almost always
unrealistic. Now the condition is that S(m,
) be independent
of m, which is almost always
unrealistic. Now the condition is that S(m,
 ) be independent of
) be independent of
 . We can expect
that, to a good approximation, this condition
will frequently hold. To the extent that it does,
Eq. (189) reduces to a Gaussian distribution of
. We can expect
that, to a good approximation, this condition
will frequently hold. To the extent that it does,
Eq. (189) reduces to a Gaussian distribution of
 about
about
 0(m
- µ(r). It follows that a standard
0(m
- µ(r). It follows that a standard
 2
minimization procedure will yield unbiased values of model parameters,
as discussed in Section 6.4.4.
2
minimization procedure will yield unbiased values of model parameters,
as discussed in Section 6.4.4.
However, the assumption that inverse Method II analyses are free of selection bias is subject to several caveats which are often overlooked:
 -dependence of the
function S(m,
-dependence of the
function S(m,
 ).
Willick (1994)
has quantified and described correction techniques for this effect.
).
Willick (1994)
has quantified and described correction techniques for this effect.
 is measured from
the HI 21 cm line. Signal-to-noise ratio
considerations can mean
that large velocity widths more likely to be undetected at low 21 cm
flux levels
(Roth 1993).
Willick et al. (1995a)
have attempted to estimate this effect for the
Mould et al. (1991)
TF sample, and found it small but non-negligible.
is measured from
the HI 21 cm line. Signal-to-noise ratio
considerations can mean
that large velocity widths more likely to be undetected at low 21 cm
flux levels
(Roth 1993).
Willick et al. (1995a)
have attempted to estimate this effect for the
Mould et al. (1991)
TF sample, and found it small but non-negligible.
6.5.5. Inverse DIs: Malmquist Bias
An inverse Method I analysis is fully analogous to a forward Method I
analysis, except that the inferred distances are obtained by solving
the equation
 0(m
- 5logd )=
0(m
- 5logd )=  implicitly for d. For the
linear inverse TF relation Eq. (168), this gives
d = 100.2[m - (D -
implicitly for d. For the
linear inverse TF relation Eq. (168), this gives
d = 100.2[m - (D -
 /e)], which
may be compared with the forward inferred distance
d = 100.2[m - (A -
b
/e)], which
may be compared with the forward inferred distance
d = 100.2[m - (A -
b ]. Although
we have used
the symbol d for both the forward and inverse inferred distance, the
two are not equal in general; the non-equality of the forward and
inverse TF parameters (Section 6.4.4) guarantees
this. In fact,
inverse DIs are steeper than their forward counterparts when
plotted in the usual way (M vs.
]. Although
we have used
the symbol d for both the forward and inverse inferred distance, the
two are not equal in general; the non-equality of the forward and
inverse TF parameters (Section 6.4.4) guarantees
this. In fact,
inverse DIs are steeper than their forward counterparts when
plotted in the usual way (M vs.
 ). Inverse
inferred distances
are thus larger for luminous, and smaller for faint, galaxies. Since
luminous objects dominate a sample at large redshifts, it is clear
that a redshift vs. inferred distance diagram will look different
depending on whether the forward or inverse relation has been used,
with quite different biases in the two cases. Let us now quantify
these ideas.
). Inverse
inferred distances
are thus larger for luminous, and smaller for faint, galaxies. Since
luminous objects dominate a sample at large redshifts, it is clear
that a redshift vs. inferred distance diagram will look different
depending on whether the forward or inverse relation has been used,
with quite different biases in the two cases. Let us now quantify
these ideas.
If we begin with Eq. (188) and go through a series of steps analogous to those which took us from Eq. (171) through Eq. (182), we obtain the following for the probability distribution of the true distance of a galaxy with inverse inferred distance d:
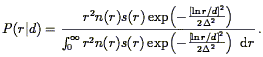
| (190) |
Here



 /e, the
effective fractional inverse
distance error, is roughly but not precisely equal to its forward
counterpart. Derivation of Eq. (190) required the
assumption of a linear inverse TF, and also of a selection function at
most weakly dependent upon
/e, the
effective fractional inverse
distance error, is roughly but not precisely equal to its forward
counterpart. Derivation of Eq. (190) required the
assumption of a linear inverse TF, and also of a selection function at
most weakly dependent upon
 (details are
given in
Willick 1995).
With these (realistic) assumptions Eq. (190)
resembles its forward analogue Eq. (182), but with a crucial
difference: the presence of the real space selection function
(details are
given in
Willick 1995).
With these (realistic) assumptions Eq. (190)
resembles its forward analogue Eq. (182), but with a crucial
difference: the presence of the real space selection function
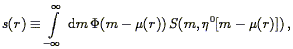
| (191) |
the probability that a
sample object lies at true distance r irrespective
of the observables (m,
 ).
).
Eq. (190) shows that the inverse Malmquist effect
quantitatively resembles the forward, with the exception that now the
product n(r)s(r) replaces n(r)
alone. The differences between
inverse and forward Malmquist bias are most clearly illustrated by
considering the uniform density case, with the further assumption that
s(r) varies slowly on scales
d . By analogy with
Eq. (185) it is then easy to derive the result
. By analogy with
Eq. (185) it is then easy to derive the result
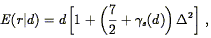
| (192) |
where
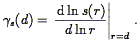
| (193) |
We see again that, like their forward counterparts, inverse inferred
distances are biased:
E(r| d)  d. However, in contrast with the
forward case, the effect is not independent of sample selection
or the luminosity function. Even in the case of uniform density, it
is not simple to obtain a Malmquist correction for an inverse
distance. One must not only accurately model the selection function
S(m,
d. However, in contrast with the
forward case, the effect is not independent of sample selection
or the luminosity function. Even in the case of uniform density, it
is not simple to obtain a Malmquist correction for an inverse
distance. One must not only accurately model the selection function
S(m,
 ), but integrate
it with respect to a believable luminosity
function
), but integrate
it with respect to a believable luminosity
function  (M). These
difficulties are only compounded by the
realistic requirement of estimating n(r) in order to
account for
IHM. The net effect of these considerations is that inverse DIs are
less suitable than forward DIs for Method I analyses. This point must
be kept in mind when one speaks of the "unbiased" character of
inverse DIs. The quantity s(r) might be modeled by the
observables
s(z) or s(d ), and thus perhaps be dealt
with easily. There is,
however, a method which, at least in principle, permits effective use
of inverse inferred distances, as we discuss in the next section.
(M). These
difficulties are only compounded by the
realistic requirement of estimating n(r) in order to
account for
IHM. The net effect of these considerations is that inverse DIs are
less suitable than forward DIs for Method I analyses. This point must
be kept in mind when one speaks of the "unbiased" character of
inverse DIs. The quantity s(r) might be modeled by the
observables
s(z) or s(d ), and thus perhaps be dealt
with easily. There is,
however, a method which, at least in principle, permits effective use
of inverse inferred distances, as we discuss in the next section.
6.5.6. The Method of Landy and Szalay
A severe obstacle to correcting for IHM is the requirement of knowing the number density n(r) along any given line of sight. One way around this obstacle is to estimate n(r) from redshift survey information. This has been done, for example, in comparisons of the IRAS density field with the POTENT mass reconstruction (Dekel et al. 1993 ; Hudson 1994a ; Hudson et al. 1995). Although reasonable, this procedure has unsatisfactory features, such as uncertainties introduced by smoothing and the need for an assumed peculiar velocity field to convert redshift- to real-space density. One would like, if possible, to derive the IHM correction self-consistently from the DI data themselves. Such a method was outlined by Landy & Szalay (1992; LS), and independently by Willick (1991) . The LS technique relies on the mathematical relationship between E(r| d) and a quantity which is in principle observable: the number of objects per unit inferred distance.
Let us define f (d) as the number of objects, per unit solid angle along a particular line of sight, per unit inferred distance. If the galaxy distribution is densely enough sampled, one can imagine measuring f (d) by binning objects in inferred distance. The resulting histogram representation of f (d) is proportional to the probability, P(d), that an object along the given line of sight has inferred distance d. This probability may in turn be calculated by integrating P(r, d ), given by Eq. (181) in the forward case and derivable from Eq. (188) in the inverse case, over the true distance r:
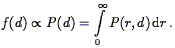
| (194) |
At this point, the expressions for the forward and cases diverge, and we present separately the result for each:
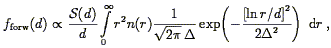
| (195) |
and
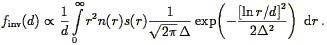
| (196) |
In the forward case, the quantity
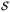 (d), which dropped out
of the
conditional expectation E(r| d), is present here in
the expression
for f (d). In the inverse case, however, f
(d) contains a dependence
on selection identical to that seen in E(r|
d). Thus, it is only for
the inverse case that the relationship between f (d) and
E(r| d) will be straightforward (cf.,
Teerikorpi 1993),
and we consider only
the inverse case (now without a subscript) in what follows.
(d), which dropped out
of the
conditional expectation E(r| d), is present here in
the expression
for f (d). In the inverse case, however, f
(d) contains a dependence
on selection identical to that seen in E(r|
d). Thus, it is only for
the inverse case that the relationship between f (d) and
E(r| d) will be straightforward (cf.,
Teerikorpi 1993),
and we consider only
the inverse case (now without a subscript) in what follows.
Taking as usual x = r/d we have
| (197) |
for inverse distances. To relate this to E(r| d) we rely on the mathematical identity (e.g., LS or Willick 1995) that
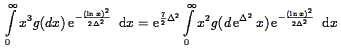
| (198) |
where g(r) is an arbitrary function. Combining Eqs. (183), (197), and (198) one readily obtains
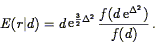
| (199) |
Eq. (199) is the basis of the Landy-Szalay method of Malmquist bias correction. It says that we can obtain an unbiased estimate of the true distance, given an inverse inferred distance d, from the observable distribution f (d).
The LS method is attractive for several reasons. First, as already
noted, it enables us to correct for IHM using the DI data alone.
Second, because LS involves inverse DI distances, it is based on a DI
relation whose calibration was very nearly free of selection
bias. In this sense, inverse DIs can be viewed as (nearly) bias-free,
but only when the LS method is used. Finally, while we have not made
this explicit in the above derivation, the LS method is applicable
even when the Gould effect is present. This is because even when the
selection function is of the form S(m,
 , r), one
arrives at the expression Eq. 190.
, r), one
arrives at the expression Eq. 190.
With this rosy view of LS must go several realistic caveats. Accurate determination of the quantity f (d) presents a number of technical problems (Willick 1995). Basically, the issue is one of resolution: one needs a sufficient number of objects per bin that the histogram representation of f (d) is not overwhelmed by shot noise; to obtain this number one must make bigger bins in both angle and distance. The larger the bin, of course, the less accurately one determines the actual IHM correction. For these reasons, LS has yet to be implemented for a real sample. An effort is presently underway (Dekel et al. 1995) to do so for the large TF samples currently available (Section 7.2). It remains unclear at this time whether implementation of the LS method will constitute a major advance in dealing with Malmquist bias.
20
Babul et al. (1994)
point out that in
certain scenarios of non-gravitational growth of structure,
Eqs. (149) and (150) might apparently be
satisfied, yielding an incorrect value of
 (Section 8.2).
Back.
(Section 8.2).
Back.
21 Often the "distance-independent" quantity is in fact weakly distance-dependent. An example is surface brightness, which falls off with increasing redshift as (1 + z)-4. However, as in that example, it is usually the case that the weak distance-dependence is either exactly or adequately modeled in terms of the redshift alone, and thus is easy to compensate for. Back.
22 The members of this second collaboration were D. Burstein, R. Davies, A. Dressler, S. Faber, D. Lynden-Bell, R. Terlevich, and G. Wegner. As a group they became widely known among astronomers as the "7 Samurai" (hereafter 7S). Back.
23 However, it was discovered that evolutionary effects are equally as important as those due to cosmology. See Sandage (1988) for a review. Back.
24 We use the term "inference," rather than the stronger "prediction" (as is used, for example, by Burstein [1990]), to underscore the fact that redshift-independent distances are merely statistical estimators, obtained from more basic measurements, of true distances--and not very accurate ones at that. Back.
25 Here we use "averaged" in its widest sense, including smoothing or modeling techniques. Back.
26 This last statement neglects second-order changes in the peculiar velocity field; cf. Willick 1991 for details. Back.
27 It is not fundamental to our definition of Method I that the TF relation be calibrated a priori. However, unnecessary complications arise if the TF parameters are considered "free." Back.
28 For pure standard candles, there is no distinction between forward and inverse methods; the material discussed in this section is only relevant for distance indicators which depend on a distance-independent observable such as line width. Back.
29 It is not, of course,
literally correct that the true distance is specified in a Method II
analysis. Errors in the velocity model being fit to the data, as well
as small-scale "noise" in the actual velocity field, mean that r
is only approximately specified by redshift information. However, to
first order this only increases the variance, but does not bias, a
Method II solution. The formalism presented above is correct in this
approximation, but the quantity
 should be regarded as the
quadrature sum of DI scatter and model errors. In
Section 8.1.3
we will describe a method which aims to go beyond this first order
approximation and include the effect of model errors and velocity
noise.
Back.
should be regarded as the
quadrature sum of DI scatter and model errors. In
Section 8.1.3
we will describe a method which aims to go beyond this first order
approximation and include the effect of model errors and velocity
noise.
Back.
30 A related complication is that not
only the
expected apparent magnitude, but also its variance is biased, in the
sense that the actual variance is strictly <
 2. The causes of
this effect, known as dispersion bias, were discussed in
Section 6.4.2. Quantitative expressions for
dispersion bias are given by
Willick (1994) .
Back.
2. The causes of
this effect, known as dispersion bias, were discussed in
Section 6.4.2. Quantitative expressions for
dispersion bias are given by
Willick (1994) .
Back.