3.1. Tremaine-Gunn bound

Before treating the phase space evolution, we discuss another important consequence of finite neutrino thermal speed: high-speed neutrinos cannot be tightly packed into galaxy halos. This fact can be used to place a lower bound on the neutrino mass if neutrinos make up the dark matter in galaxy halos (Tremaine & Gunn 1979).

The initial phase space density for massive neutrinos is a relativistic Fermi-Dirac distribution (preserved from the time when the neutrinos decoupled in the early universe):

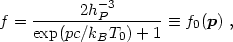(3.4)

where p is the comoving canonical momentum of eq. (1.13), h_P is Planck's constant (with a subscript to distinguish it from the scaled Hubble constant), and T₀ = aT is the present neutrino "temperature." The decrease of T with time is compensated for by the factor a relating proper momentum to comoving momentum. Ignoring perturbations, the present-day distribution for massive neutrinos is the relativistic Fermi-Dirac - not the equilibrium nonrelativistic distribution - because the phase space distribution was preserved after neutrino decoupling.

Tremaine & Gunn (1979) noted that because of phase mixing (discussed further below), the maximum coarse-grained phase space density of massive neutrinos today is less than the maximum of f₀(p), h_P^-3. If massive neutrinos dominate the mass in galactic halos, this must be no less than the phase space density needed for self-gravitating equilibrium. This bound can be used to set a lower limit on the neutrino mass if one assumes that the neutrinos constitute the halo dark matter.

Although the neutrino mass bound is somewhat model-dependent because the actual coarse-grained distribution in galactic halos is unknown, we can get a reasonable estimate by assuming an isothermal sphere: a Maxwell-Boltzmann distribution with constant velocity dispersion ² (at a = 1 so that there is no distinction between proper and comoving):

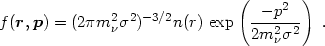(3.5)

In a self-gravitating system there are a family of spherical density profiles (r) = m n(r) obeying hydrostatic equilibrium:

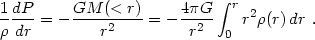(3.6)

The simplest case is the singular isothermal sphere with r^-2; the reader can easily check that = ² / (2 Gr²). Imposing the phase space bound at radius r then gives

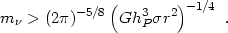(3.7)

Up to overall numerical factors, this is the Tremaine-Gunn bound.

The singular isothermal sphere is probably a good model where the rotation curve produced by the dark matter halo is flat, but certainly breaks down at small radius. Because the neutrino mass bound is stronger for smaller r², the uncertainty in the halo core radius (interior to which the mass density saturates) limits the reliability of the neutrino mass bound.

For the Local Group dwarf galaxies in Draco and Ursa Minor, measurements of stellar velocity dispersions suggest is a few to about 10 km s^-1 (Pryor & Kormendy 1990). If these galaxies have isothermal halos at r = 1 kpc, the crude bound of eq. (3.7) implies m is greater than a few eV.