


3.2. Vlasov equation
We now present a rigorous treatment of the evolution of perturbations
in a nonrelativistic collisionless gas, based on the evolution of the phase
space distribution. The single-particle phase space density
f(x, p,
 ) is defined so that
fd3 xd3 p is the number of
particles in
an infinitesimal phase space volume element. We shall use comoving spatial
coordinates x and the associated conjugate momentum
p = am
) is defined so that
fd3 xd3 p is the number of
particles in
an infinitesimal phase space volume element. We shall use comoving spatial
coordinates x and the associated conjugate momentum
p = am
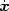 (eq. 1.13). Note that
d3 xd3 p =
m3 d3 rd3 v
is a proper quantity so that f is the proper (physical) phase
space density.
(eq. 1.13). Note that
d3 xd3 p =
m3 d3 rd3 v
is a proper quantity so that f is the proper (physical) phase
space density.
If the gas is perfectly collisionless, f obeys the Vlasov (or collisionless Boltzmann) equation of kinetic theory,
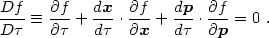 |
(3.8) |
This equation expresses conservation of particles along the phase space
trajectory
{x( ),
p(
),
p( )}. Using
Hamilton's equations
(1.16) for nonrelativistic particles, we obtain
)}. Using
Hamilton's equations
(1.16) for nonrelativistic particles, we obtain
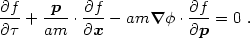 |
(3.9) |
The Vlasov equation is supposed to apply for the coarse-grained phase space density for a collisionless gas in the absence of two-body correlations (Ichimaru 1992). Often, however, the statistical assumptions underlying the use of the Vlasov equation are vague. To clarify its application we digress to present a derivation using the Klimontovich (1967) approach to kinetic theory.
Consider one realization of a universe filled with particles following
phase space trajectories
{xi( ),
pi(
),
pi( )}
(i labels
the particles). The exact single-particle phase space density
(called the Klimontovich density) is written by summing over Dirac
delta functions:
)}
(i labels
the particles). The exact single-particle phase space density
(called the Klimontovich density) is written by summing over Dirac
delta functions:
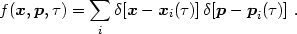 |
(3.10) |
No statistical averaging or coarse-graining has been applied; f is the fine-grained density for one universe. This phase space density obeys the Klimontovich (1967) equation, which is of exactly the same form as eq. (3.8). The proof follows straightforwardly from substituting eq. (3.10) into eq. (3.8).
The Klimontovich density retains all information about the microstate of a system because it specifies the trajectories of all particles. This is far too much information to be practical. We must reduce the information content by performing some averaging or coarse-graining. This averaging is taken over a statistical ensemble of microstates corresponding to a given macrostate - for example, microstates with the same phase space density averaged over small phase space volumes containing many particles on average. We denote the averages using angle brackets <>, without being very precise about the ensemble adopted for the coarse-graining.
The discreteness effects of individual particles are accounted for by the s-particle distribution functions (s = 1, 2, ...) fs, which are defined using a standard cluster expansion:
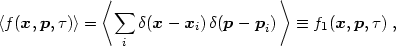 |
(3.11) |
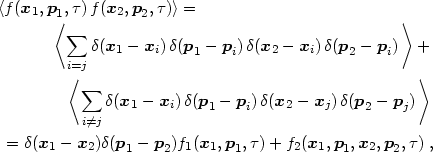 |
(3.12) |
and so on. We further write f2 as a sum of uncorrelated and correlated parts,
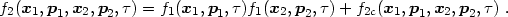 |
(3.13) |
This equation defines f2c, known in kinetic theory as the irreducible two-particle correlation function. If there are no pair correlations in phase space, f2c = 0.
We now ensemble-average the Klimontovich equation, recalling that it
is identical to eq. (3.9) provided we use the Klimontovich
density. If  is
a specified external potential, neglecting self-gravity,
we see that f1 obeys the Vlasov equation. However, if
is
a specified external potential, neglecting self-gravity,
we see that f1 obeys the Vlasov equation. However, if
 is computed
self-consistently from the particles, the
m
is computed
self-consistently from the particles, the
m
 .
(
.
( f /
f /
 p)
term is quadratic in the Klimontovich density, yielding an
additional correlation term from eqs. (3.12) and (3.13) after
coarse-graining. This term is not present in the Vlasov equation.
p)
term is quadratic in the Klimontovich density, yielding an
additional correlation term from eqs. (3.12) and (3.13) after
coarse-graining. This term is not present in the Vlasov equation.
The contribution to the gravity field from the particles is (cf. eq. 1.11)
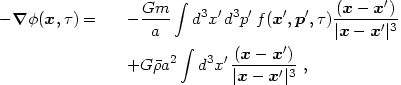 |
(3.14) |
where the second term, required in comoving coordinates, removes the contribution from the mean uniform background.
Combining our results now yields the exact kinetic equation for the one-particle phase space density f1:
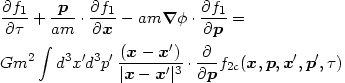 |
(3.15) |
where - 
 is given by
eq. (3.14) using
f1 for f, and adding any other contribution
from other sources.
Equation (3.15) is called the first BBGKY hierarchy equation
(Peebles 1980,
Ichimaru 1992).
It differs from the Vlasov equation by a correlation integral term.
is given by
eq. (3.14) using
f1 for f, and adding any other contribution
from other sources.
Equation (3.15) is called the first BBGKY hierarchy equation
(Peebles 1980,
Ichimaru 1992).
It differs from the Vlasov equation by a correlation integral term.
If there are no phase space correlations, as would occur if we had a
smooth collisionless fluid, then the one-particle or coarse-grained
distribution obeys the Vlasov equation of kinetic theory. Correlations
may be introduced by gravitational clustering, which couples
f2c
to f1. One may derive an evolution equation for
f2c - the second BBGKY hierarchy equation - by averaging
f f /
f /

 ,
but it involves f3c, and so on. The result is an
infinite hierarchy of coupled kinetic equations, the BBGKY hierarchy.
,
but it involves f3c, and so on. The result is an
infinite hierarchy of coupled kinetic equations, the BBGKY hierarchy.
For some cases, Boltzmann's hypothesis of molecular chaos may hold, implying f2c = 0 except at binary collisions, with the right-hand side of eq. (3.15) becoming a Boltzmann collision operator. Fortunately, for the particles of interest here - neutrinos - the gravitational (and non-gravitational, after neutrino decoupling) collision time is so long that the correlation integral is completely negligible. Thus, hot dark matter composed of massive neutrinos obeys the Vlasov equation after decoupling. From now on we shall drop the subscript 1 from f.
We now return to our main line of development to discuss phase mixing. The Vlasov equation implies conservation of phase space density, but a given initial volume d3xd3p evolves in a complicated way (i.e., the trajectories of particles initially inside this volume may be highly complicated). Consider the initial phase space element shown in Figure 2a, extracted from a one-dimensional N-body simulation. Figures 2b and 2c show the phase space distribution at a later time, with each particle's trajectory evolved according to Hamilton's equations without (Fig. 2b) and with (Fig. 2c) gravity, respectively. In both cases the area dxdp of the phase space element is identical to the initial area as a consequence of the Vlasov equation.
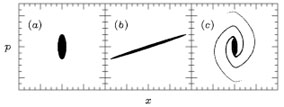 |
Figure 2. Phase space evolution. (a) Initial conditions. (b) Evolved state without gravity. (c) Evolved state with gravity. |
Figure 2c illustrates the process known as phase mixing: the phase space structure becomes highly convoluted as particles make multiple orbits. Regions of initially high phase space density can end up entwined with regions of initially low phase space density. Although the density is conserved along each phase space trajectory, if the distribution is coarse-grained (averaged over finite phase space volume), the resulting coarse-grained density is not conserved. The maximum coarse-grained density can only decrease, as we noted previously in the discussion of the Tremaine-Gunn bound.
The process of phase-mixing is complicated, and the only practical means of integrating the Vlasov equation for such an evolved collisionless system is by N-body simulation: the phase space is sampled with discrete particles at some initial time and the particle trajectories are computed, providing a sample of the evolved phase space. However, analytical methods can be used while the phase space distribution is only slightly perturbed from the homogeneous equilibrium distribution. These methods, presented in the next two subsections, will help us to understand free-streaming damping in detail.