


The projected luminosity profiles of elliptical galaxies are well approximated by de Vaucouleurs' r1/4 law,
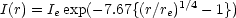 |
(2.1) |
(de Vaucouleurs, 1959). Here, Ie is the intensity at the effective radius re which encloses half the total light. A number of fitting functions have been proposed such as the Hubble law, I = I0 / (r + a)2 (Hubble, 1930), and the King (1966) models. The King and de Vaucouleurs profiles are compared in Figure 2.1. Note that the main differences between the curves are at small separations, where King profiles flatten off but the r1/4 profile continues to rise. At larger radii, the profiles are in close agreement. Equation (2.1) has been found to accurately represent the luminosity profiles of ellipticals over a wide range of radii (de Vaucouleurs and Capaccioli, 1979). It has the added advantage that the parameter re (for nearby galaxies) is usually much larger than 1 arcsec and is unaffected by the blurring of the galaxy image due to turbulence in the Earth's atmosphere. (This blurring is usually called "seeing".) In contrast, the parameter a of Hubble's law and the core radius of King's models are often comparable to the radius of the seeing disc and are, therefore, more difficult to determine accurately (Schweizer, 1979). Because of the effects of seeing, there is some controversy at present as to whether elliptical galaxy profiles flatten off at small radii as in the King models, or continue to rise as in the r1/4 law.
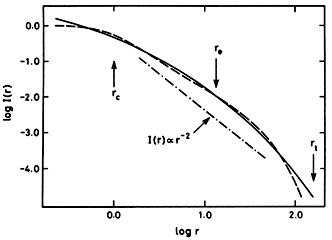 |
Figure 2.1. Comparison of two fitting functions commonly used to characterize the luminosity profiles of elliptical galaxies. The solid line shows a de Vaucouleurs profile with effective radius re and the dashed line shows a King (1966) model with core radius rc and tidal radius rt. The units of intensity are arbitrary (adapted from King, 1966). |
The effective radius has been found to correlate with the total luminosity (measured in the B-band)
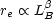 |
(2.2) |
but there is some uncertainty in the value of the exponent
 . From
Kormendy's (1977a)
sample of normal ellipticals, one finds
. From
Kormendy's (1977a)
sample of normal ellipticals, one finds

 0.8 and
Tonry and Davis
(1981a) and
Davies et
al. (1983) find
0.8 and
Tonry and Davis
(1981a) and
Davies et
al. (1983) find

 0.6
using data from the Second Reference Catalogue of Bright Galaxies
(de Vaucouleurs, de
Vaucouleurs and Corwin, 1976).
0.6
using data from the Second Reference Catalogue of Bright Galaxies
(de Vaucouleurs, de
Vaucouleurs and Corwin, 1976).
The three-dimensional space density profile for a spherical galaxy may be readily obtained from the two-dimensional profile I(s).
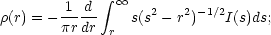 |
(2.3) |
hence, a projected profile that falls off as r-2
implies a space density profile
 (r)
(r)
 r-3.
r-3.
There are some ellipticals which do show deviations from the de Vaucouleurs profile (see Kormendy, 1977a). These are usually the brightest members of rich clusters of galaxies (the D type galaxies of Matthews, Morgan and Schmidt, 1964) which possess an extensive outer envelope.
The ellipticity profiles vary considerably. In most cases, the ellipticity increases with increasing radius, but there exist a number of galaxies in which the reverse occurs (Carter, 1978; King, 1978; Leach, 1981). In addition, there are several galaxies in which the position angle of the best fitting ellipse at any given isophote changes with radius (Evans, 1951; King, 1978; Carter, 1978; Leach, 1981). This effect may be understood if elliptical galaxies possess triaxial isodensity contours. The isophote twist may then result if the galaxy possesses an ellipticity gradient and is seen in projection along an axis that does not coincide with one of the principal axes. The question of whether ellipticals more nearly resemble prolate or oblate spheroids is still unanswered, though several tests have been proposed (Marchant and Olson, 1979; Richstone, 1979; Lake, 1980).