


2.1.2. Rotaional properties
It used to be widely believed that elliptical galaxies were oblate
spheroids and that their flattening was due to rotation, in analogy
with the rotating figures of equilibrium of incompressible fluids (e.g.,
Chandrasekhar, 1969).
The relationship between rotational
velocity and ellipticity of an oblate spheroid with constant
ellipticity
 is
(Binney (1978)),
is
(Binney (1978)),
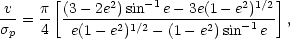 |
(2.4) |
where e2 = 1 - (1 -
 )2,
v is the rotational velocity assumed to be
constant and
)2,
v is the rotational velocity assumed to be
constant and  p
is the projected velocity dispersion also assumed to
be constant. (1)
The above relationship has been shown by Binney to apply
independently of the form of the density profile.
p
is the projected velocity dispersion also assumed to
be constant. (1)
The above relationship has been shown by Binney to apply
independently of the form of the density profile.
 |
Figure 2.2. The ratio of the maximum
rotational velocity vm to the mean
velocity dispersion in the central regions
|
In the last few years, rotation curves and velocity dispersion
profiles have been obtained for a large number of elliptical galaxies
(see e.g.
Illingworth, 1981
and references therein), and it is quite
clear that most giant ellipticals rotate much more slowly than
predicted by Eq. (2.4). The observational results are summarized in
Figure 2.2. There are two possible
explanations of the
results. Ellipticals may be prolate and rapidly rotating, or their
flattening may be due to velocity anisotropies rather than
rotation. For rapidly rotating prolate spheroids, projection effects
will lead to a large spread in
v /  at any given
ellipticity.
Binney (1978)
has calculated a median curve (shown as the dotted line in
Figure 2.2). If ellipticals are prolate and
rapidly rotating, about
half of the observed points should lie above the line and half should
lie below. The observations are inconsistent with this hypothesis,
therefore, the flattening of many ellipticals must be due to velocity
anisotropies. Recently, it has been found that it is the more luminous
elliptical galaxies which rotate slowly
(Davies et al., 1983).
In Figure 2.3 we show the ratio of the
observed value of v /
at any given
ellipticity.
Binney (1978)
has calculated a median curve (shown as the dotted line in
Figure 2.2). If ellipticals are prolate and
rapidly rotating, about
half of the observed points should lie above the line and half should
lie below. The observations are inconsistent with this hypothesis,
therefore, the flattening of many ellipticals must be due to velocity
anisotropies. Recently, it has been found that it is the more luminous
elliptical galaxies which rotate slowly
(Davies et al., 1983).
In Figure 2.3 we show the ratio of the
observed value of v /
 to that
predicted on the oblate model (Eq. 2.4) as a function of absolute
magnitude. There is a significant correlation, showing that the
rotational properties of ellipticals depend on luminosity. A rough
approximation to these results is the power-law relation,
to that
predicted on the oblate model (Eq. 2.4) as a function of absolute
magnitude. There is a significant correlation, showing that the
rotational properties of ellipticals depend on luminosity. A rough
approximation to these results is the power-law relation,
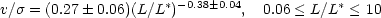 |
(2.5) |
where we have taken L* = 1.1 ×
1010h-2
L in the
B-band (2).
in the
B-band (2).
 |
Figure 2.3. The ratio of the observed value
of vm /
|
1 This equation may be approximated by
the simple formula
v /  p
= [
p
= [ / (1 -
/ (1 -
 )]1/2.
Back.
)]1/2.
Back.
2 Here and throughout this article h denotes Hubble's constant H0 in units of 100 km s-1 Mpc-1. Planck's constant is denoted by hp. Back.