


2.1.3. Correlations between luminosity, velocity dispersion and metallicity
Faber and Jackson (1976) found that the central velocity dispersions of elliptical galaxies are related to luminosity according to,
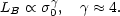 |
(2.6) |
Many more data have become available recently
(Tonry and Davis, 1981a,
Tonry and Davis, 1981b
and references therein), but the uncertainty in the exponent
 is quite large
is quite large 

 ± 1. This is
because the scatter in the relation is
much larger than that expected from the observational errors
alone. The errors in the velocity dispersions are usually small
(
± 1. This is
because the scatter in the relation is
much larger than that expected from the observational errors
alone. The errors in the velocity dispersions are usually small
(  10%). The
uncertainties in the calculation of luminosities are much
more difficult to estimate as there may be systematic errors tn
calculating distances to nearby galaxies due to the peculiar velocity
of the Local Group induced by the Virgo cluster. Using a simple model
for the infall velocity field, Tonry and Davis find that the scatter
is minimized if the Local Group has an infall velocity of 470 ± 70 km
sec-1. Because of possible systematic effects it is difficult
to judge the accuracy of the infall velocity deduced in this way. A recent
analysis, using the relation between HI width and infrared luminosity
for spiral galaxies yields a somewhat lower value of ~ 300 km
sec-1
(Aaronson et al.,
1982).
10%). The
uncertainties in the calculation of luminosities are much
more difficult to estimate as there may be systematic errors tn
calculating distances to nearby galaxies due to the peculiar velocity
of the Local Group induced by the Virgo cluster. Using a simple model
for the infall velocity field, Tonry and Davis find that the scatter
is minimized if the Local Group has an infall velocity of 470 ± 70 km
sec-1. Because of possible systematic effects it is difficult
to judge the accuracy of the infall velocity deduced in this way. A recent
analysis, using the relation between HI width and infrared luminosity
for spiral galaxies yields a somewhat lower value of ~ 300 km
sec-1
(Aaronson et al.,
1982).
The effects of magnitude errors may be reduced if one studies
galaxies which are known to be at the same distance.
Tonry (1981)
has recently obtained results from a complete sample of 20 elliptical
galaxies in the core of the Virgo cluster. He finds an extremely tight
correlation and derives a slope of
 = 3.2
± 0.2. This is not
inconsistent with previous results. As Tonry points out, the sample
contains a much larger fraction of low luminosity ellipticals than did
previous samples so this result may just indicate a general curvature
in the relation, the brighter galaxies following
L
= 3.2
± 0.2. This is not
inconsistent with previous results. As Tonry points out, the sample
contains a much larger fraction of low luminosity ellipticals than did
previous samples so this result may just indicate a general curvature
in the relation, the brighter galaxies following
L 
 04
and the low
luminosity galaxies following a steeper relation. Tonry's sample is
too small to make a convincing test of this hypothesis.
04
and the low
luminosity galaxies following a steeper relation. Tonry's sample is
too small to make a convincing test of this hypothesis.
What does Eq. (2.6) tell us about elliptical galaxies? We know from surface photometry that the luminosity profiles depend on only one length scale, re. If we make the assumption that the mass-to-light ratio is independent of radius, then the virial theorem requires,
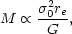 |
(2.7) |
where M is the total mass of the galaxy. Combining Eqs. (2.2), (2.6) and (2.7) we find,
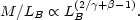 |
(2.8) |
Hence, we learn something about the relationship between
mass-to-light ratio and luminosity. Unfortunately the errors on the
indices  and
and  are
sufficiently large that the relation
cannot be tied down with any great accuracy, but it is consistent with
M/L = constant.
are
sufficiently large that the relation
cannot be tied down with any great accuracy, but it is consistent with
M/L = constant.
There also exists a correlation between central metallicity and luminosity (Faber, 1977),
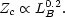 |
(2.9) |
Here Zc denotes the total abundance by mass of elements heavier than 4He.
The origin of this relation is not well understood, but it has been
suggested that chemical evolution may be dependent on the depths of
the potential wells of galaxies
(Larson, 1974a;
Tonry and Davis, 1981a).
As the gravitational binding energy may be measured using the
velocity dispersion  ,
which by Eq. (2.6) is correlated with total
luminosity, a metallicity-luminosity correlation might be
expected. Indeed, Tonry and? Davis find that the correlation between
metallicity and velocity dispersion is much better than that between
metallicity and luminosity. The relationship between metallicity,
velocity dispersion and luminosity is discussed further by
Terlevich et al. (1981)
though from a somewhat different point of view.
,
which by Eq. (2.6) is correlated with total
luminosity, a metallicity-luminosity correlation might be
expected. Indeed, Tonry and? Davis find that the correlation between
metallicity and velocity dispersion is much better than that between
metallicity and luminosity. The relationship between metallicity,
velocity dispersion and luminosity is discussed further by
Terlevich et al. (1981)
though from a somewhat different point of view.