


4.1. Damping of adiabatic fluctuations
To follow the evolution of radiation fluctuations one works with the radiation distribution function,
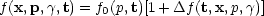 |
(4.1) |
where f0 is the blackbody distribution function,
p is the photon
momentum and
 is
the photon direction. The evolution of the radiation
distribution function is described by the Boltzmann equation, where
the dominant interaction between radiation find matter is assumed to
be Thomson scattering
(Peebles and Yu, 1970;
Peebles, 1980a).
Neglecting possible spectral distortions one may define the
frequency-averaged perturbation to the radiation brightness,
is
the photon direction. The evolution of the radiation
distribution function is described by the Boltzmann equation, where
the dominant interaction between radiation find matter is assumed to
be Thomson scattering
(Peebles and Yu, 1970;
Peebles, 1980a).
Neglecting possible spectral distortions one may define the
frequency-averaged perturbation to the radiation brightness,
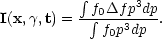 |
(4.2) |
The direction averaged perturbation to the radiation energy density is:
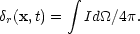 |
(4.3) |
As we discussed in Section 3, using the synchronous gauge (h00 = hi0 = 0) and decomposing the perturbation into Fourier components, the dominant mode for adiabatic perturbations on scales greater than the horizon grows as
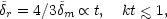 |
(4.4) |
in the radiation dominated era. Here
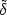 m
is the Fourier transform of
the fractional perturbation to the matter density
m
is the Fourier transform of
the fractional perturbation to the matter density
 m =
m =
 m(1 +
m(1 +
 m).
When the adiabatic perturbation enters
the horizon it begins to oscillate like an acoustic wave,
m).
When the adiabatic perturbation enters
the horizon it begins to oscillate like an acoustic wave,
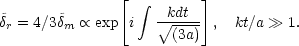 |
(4.5) |
This result is valid if the matter and radiation can be treated as an
ideal fluid. The mean free time for Thomson scattering is
tc = 1 /
( T
ne), where
T
ne), where
 T is the
Thomson cross-section and ne is the free
electron density. Equation (4.5) thus requires tc =
0. Whilst
perturbations are in the optically thick regime we can derive an
analytic estimate of the damping rate of adiabatic fluctuations as follows
(Silk, 1968;
Field, 1971;
Chibishov, 1972;
Kaiser, 1983a).
If kt/a >> 1, gravity can be neglected since the
scales of interest are
well within the Jeans length. Assuming isotropic scattering, the
equation for the radiation brightness can be written as,
T is the
Thomson cross-section and ne is the free
electron density. Equation (4.5) thus requires tc =
0. Whilst
perturbations are in the optically thick regime we can derive an
analytic estimate of the damping rate of adiabatic fluctuations as follows
(Silk, 1968;
Field, 1971;
Chibishov, 1972;
Kaiser, 1983a).
If kt/a >> 1, gravity can be neglected since the
scales of interest are
well within the Jeans length. Assuming isotropic scattering, the
equation for the radiation brightness can be written as,
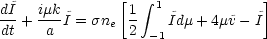 |
(4.6a) |
where µ = k .
 / |k| and
/ |k| and 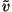 is
the Fourier transform of the matter velocity.
The force equation for the matter is,
is
the Fourier transform of the matter velocity.
The force equation for the matter is,
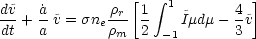 |
(4.6b) |
and the equation of continuity for the matter is
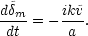 |
(4.6c) |
For a detailed derivation of these equations, including gravitational terms, see Peebles (1980a). The analysis can be further simplified if the expansion of the Universe is neglected. This is justified if the damping timescale is much shorter than the Hubble time. Equation (4.6a) may then be solved to second order in tc,
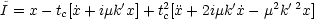 |
(4.7) |
where x =
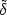 r
+ 4 µ
r
+ 4 µ 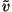 and
k' is the proper wavenumber k' = k/a. Next we
take the first moment of (4.7) and substitute into the force equation
(4.6b). The zeroth moment of (4.7) gives the fluctuation in the
energy density
and
k' is the proper wavenumber k' = k/a. Next we
take the first moment of (4.7) and substitute into the force equation
(4.6b). The zeroth moment of (4.7) gives the fluctuation in the
energy density
 r. Hence,
r. Hence,
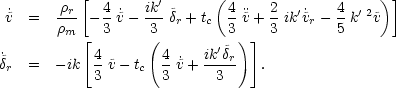 |
(4.8a) (4.8b) |
These equations have solutions
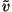 =
=
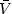 exp(
exp( i
t),
i
t),
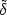 r
=
r
=  exp(
exp( i
t) where,
i
t) where,
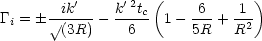 |
(4.9) |
where R = 1 +
3 m /
4
m /
4 r
(Peebles and Yu, 1970;
Weinberg, 1971).
If the polarizing property of Thomson scattering is included, one finds a
slightly larger damping rate;
r
(Peebles and Yu, 1970;
Weinberg, 1971).
If the polarizing property of Thomson scattering is included, one finds a
slightly larger damping rate;
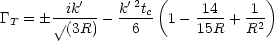 |
(4.10) |
which exceeds
 i by a
factor of 4/3 in the radiation dominated limit
(Kaiser, 1983a).
To improve on these analytical estimates, and in
particular to treat the important regime when
k'tc ~ 1,
one must resort to a detailed numerical solution of the Boltzmann equation
(Peebles and Yu, 1970;
Silk and Wilson, 1981;
Wilson and Silk, 1981;
Peebles, 1981a).
For example, Wilson and Silk expand the angular
dependence of the radiation brightness in Legendre polynomials,
i by a
factor of 4/3 in the radiation dominated limit
(Kaiser, 1983a).
To improve on these analytical estimates, and in
particular to treat the important regime when
k'tc ~ 1,
one must resort to a detailed numerical solution of the Boltzmann equation
(Peebles and Yu, 1970;
Silk and Wilson, 1981;
Wilson and Silk, 1981;
Peebles, 1981a).
For example, Wilson and Silk expand the angular
dependence of the radiation brightness in Legendre polynomials,
 |
(4.11) |
and integrate the equations for
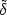 l(t) numerically until some
time tf when
the optical depth to the observer is small. For a given wavenumber
k' one requires N ~ k' tf
spherical harmonics for an accurate
description. Thus for large wavenumbers, Wilson and Silk took N =
99. Alternative numerical techniques have been presented by
Peebles and Yu (1970),
Peebles (1981a),
Kaiser (1983a) and
Wyse and Jones (1983).
l(t) numerically until some
time tf when
the optical depth to the observer is small. For a given wavenumber
k' one requires N ~ k' tf
spherical harmonics for an accurate
description. Thus for large wavenumbers, Wilson and Silk took N =
99. Alternative numerical techniques have been presented by
Peebles and Yu (1970),
Peebles (1981a),
Kaiser (1983a) and
Wyse and Jones (1983).
 |
Figure 4.1. Summary of results of numerical
computations of the damping of adiabatic fluctuations. The damping mass
is defined as MD =
4 |
The results from several numerical calculations are summarized in Figure 4.1. These calculations yield a characteristic damping mass,
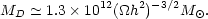 |
(4.12) |
The damping process therefore results in the imposition of a
characteristic feature on the fluctuation spectrum at a mass scale
corresponding to groups or clusters of galaxies. Since the
fluctuations are linear, each Fourier component evolves independently
and so the damping effects may be summarized in terms of a linear
transfer function T(k) =
|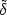 m(tf) /
m(tf) /
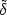 m(ti)| where
m(ti)| where
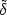 m(ti) is the Fourier transform
of the matter density perturbation specified at some early time
ti. The transfer function is, therefore, independent
of the shape of the initial fluctuation spectrum.
m(ti) is the Fourier transform
of the matter density perturbation specified at some early time
ti. The transfer function is, therefore, independent
of the shape of the initial fluctuation spectrum.
In Figure 4.2 we show k3/2
|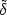 m(tf)| assuming an
initial power-spectrum
|
m(tf)| assuming an
initial power-spectrum
|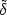 m|2
m|2
 kn
with n = + 1. The peaking on the largest scale, corresponding
to the horizon size at decoupling, is especially prominent if
kn
with n = + 1. The peaking on the largest scale, corresponding
to the horizon size at decoupling, is especially prominent if
 = 1
since the Jeans mass is well within the horizon mass ~ 1016.8
(
= 1
since the Jeans mass is well within the horizon mass ~ 1016.8
( h2)-1/2
M
h2)-1/2
M at decoupling. For the lower
at decoupling. For the lower
 (= 0.1) case shown,
there is less time
for any preferential large-scale growth to occur, since the Universe
only becomes matter-dominated just prior to decoupling.
(= 0.1) case shown,
there is less time
for any preferential large-scale growth to occur, since the Universe
only becomes matter-dominated just prior to decoupling.
 |
Figure 4.2. Density fluctuation spectrum
| |
It has been argued that the drastic decrease in sound velocity at decoupling leads to supersonic compressional motions and consequently to a large amplification of adiabatic density fluctuations by up to a factor ~ 100 over galactic mass-scales (Sunyaev and Zel'dovich, 1970; Doroshkevich, Sunyaev and Zel'dovich, 1974). However, the detailed numerical studies have not shown this effect. In reality, Compton drag due to the residual ionization during decoupling strongly damps any supersonic motions, and hence there is little net amplification.