3.3. Shape of the fluctuation spectrum

A common assumption to be found in the literature is that the amplitude of a fluctuation when it comes within the horizon varies as some power of the mass contained within the horizon,

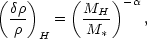(3.20)

with the power-law index , and the amplitude (fixed by M_*) as free parameters.

This hypothesis is made purely for simplicity rather than from any compelling physical reason (a hypothesis of maximal ignorance). Zel'dovich (1972) has suggested an adiabatic spectrum with = 0, i.e. ( / )_H = K where K is some constant. The motivation behind this choice of spectrum (often referred to as constant curvature fluctuations) is that it presents no preferred scales. Zel'dovich argues that the constant K might be related to the total entropy per baryon, the entropy being generated by the damping of short wavelength perturbations (though see Barrow and Matzner, 1977). If we choose < 0, it implies that the Universe is non-Friedmannian with divergent curvature perturbations on large scales. If > 0, it implies that the Universe was non-Friedmannian at early times. In the latter case it is likely that order-unity fluctuations on scales of the horizon would lead to a prolific production of black holes with masses M_* (Carr, 1975; Barrow and Carr, 1978) (and a cosmological density in black holes _{black hole} >> 1) and would disrupt the standard picture of nucleosynthesis. This is unattractive, but in order to avoid these problems, some physical process is required which cuts off the spectrum (3.20) such that / << 1 for M M_* (Press and Vishniac, 1980b).

Gott and Rees (1975) suggested an initial spectrum of isothermal perturbations obeying the Zel'dovich constant curvature hypothesis. If we let t_equ be the epoch at which baryon and radiation densities are equal, _B(t_equ) = _R(t_equ), and M_equ is the total mass in baryons with the horizon at t_equ, then from Eq. (3.20),

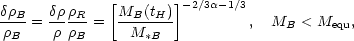(3.21)

where M_B(t_H) is the total mass in baryons within the horizon at time t_H. Gott and Rees' constant curvature hypothesis then yields _B / _B M_B^-1/3. As in the case of adiabatic perturbations, any spectrum of the form (3.20) with > 0 leads to non-Friedmannian behaviour on small scales. In the case of isothermal perturbations this occurs when perturbations are matter-dominated on horizon scales at early times. The evolution of non-linear isothermal perturbations, and their effect on primordial nucleosynthesis has been considered in some detail by Hogan (1978).

Finally we note that the observed entropy per baryon ratio may have an explanation in terms of baryon non-conserving and CP violating processes acting at very early times when T 10²⁸ K. Several authors (Weinberg, 1982; Press and Vishniac, 1980b) have made the important point that if the entropy per baryon is fixed in terms of purely microscopic parameters, then any initial isothermal perturbations would be erased, and only adiabatic fluctuations could survive. Ways out of this possible difficulty are discussed in Section 9.