7. GALAXY MERGERS

7.1. Cross-sections and merger rates

Consider the interaction of a perturbing galaxy of mass M_p with another galaxy of mass M_G. If the perturber passes by with a large velocity v, it will be a good approximation to assume that the stars in the perturbed galaxy do not move during the encounter. Using this impulsive encounter approximation (Spitzer, 1958), the velocity change of a star in the perturbed galaxy is

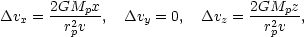(7.1)

where v is assumed to be parallel to the y-axis, and r_p is the impact parameter for the collision. The total change in the internal energy of the perturbed galaxy is

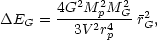(7.2)

where _G² is the mean-square radius of the perturbed galaxy. Equation (7.2) is valid if the energy change due to first order terms in v is zero (e.g. Richstone, 1976; White, 1979a). Now, if the galaxies are identical, with orbital energy E₀ = 1/4MV², Eq. (7.2) applies for each galaxy, hence (Tremaine (1981)),

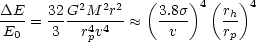(7.3)

where the relationship on the r.h.s. of Eq. (7.3) is approximately valid if the galaxies possess brightness profiles which follow the de Vaucouleurs r^1/4 law with half-mass radius r_h and a peak velocity dispersion . Equation (7.3) illustrates that in a rich cluster of galaxies, in which the typical encounter velocity is v >> , even a grazing encounter will produce a relatively small change in the total internal energy. Equations (7.1) also show that the stars in the outer parts of a galaxy will be most affected by such an encounter, with the result that some mass loss must occur. Detailed computations of this effect have been carried out by Richstone (1975, 1976 and references therein).

Now consider a slow interpenetrating encounter. Equation (7.3) then states that E / E₀ 1. The entire orbital energy will be soaked up during the encounter, and one concludes that the galaxies will merge (Alladin, 1965; Alladin et al., 1975). Clearly such an application of Eq. (7.3) violates the impulsive approximation on which it is based, but recently several numerical studies (Toomre, 1977; van Albada and van Gorkom, 1977; Roos and Norman, 1979; White, 1978, 1979b) ⁽⁹⁾ have confirmed the suspected stickiness of galaxies in low velocity encounters. The results are actually in quite good agreement with those obtained from the impulse approximation.

Results for the capture cross-sections from some of these numerical studies are summarized in Figure 7.1.

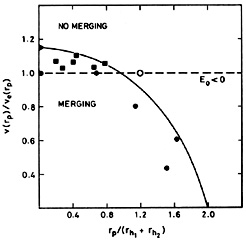Figure 7.1. Summary of numerical results on the capture cross-section. v(rp) is the relative velocity between two galaxies at the pericenter of their two-body orbit. ve(rp) is the escape velocity at pericenter. The half-mass radii of the two galaxies are rh1 and rh2. E0 is the total orbital energy. The triangle at v(0) = 1.16ve(rp) is from the numerical experiments of van Albada and van Gorkom (1977). The squares are from the numerical experiments of Roos and Norman (1979) and the filled circles are from experiments E through I of White (1978), all of which led to merging. The open circle is from White's experiment D which did not merge before the calculation was stopped. The solid line shows the capture cross-section used by Aarseth and Fall (1980) in their cosmological N-body experiments [rp / 2(rh1 + rh2)]2 + [v(rp) / 1.16ve(rp)]2 1 (from Aarseth and Fall (1980), with permission).

Although the numerical calculations have confirmed earlier suspicions that merging could occur, the possibility that they play a significant role in galaxy evolution has been seriously entertained only recently. Since the ratio of the optical half-mass radius of a typical giant galaxy to the average intergalaxy separation is extremely small, r_h / 4 × 10^-3, it was thought that a merger would be an extremely rare event. However, it now seems possible that the optical radius of a typical spiral galaxy is a very poor indicator of the mass distribution. Dark halos may contain most of the mass and extend out to perhaps over 100 kpc (Section 2.2). Because the true extent of the dark halos is uncertain it is difficult to make a reliable estimate of the current merger rate. One argument, due to Toomre (1977, also Toomre and Toomre, 1972) suggests that it is quite high. Toomre cites eleven examples from the NGC catalogue, of galaxies which appear to be currently in the process of merging. These pairs exhibit strong tidal tails and in some cases the main body of the system can hardly be separated into two distinct components. Toomre then argues that the tails must be transient phenomena with a median age of 5 × 10⁸ yr. Thus if the merger rate were constant during the past 10¹⁰ yr, one would expect 200 merger galaxies out of a total of 4000 NGC galaxies. Since the merger rate is likely to have been even higher in the past, this number could even be a considerable underestimate. It does than appear possible that mergers have been important in determining the morphology of galaxies and it is relevant to ask what merger remnants might look like now and also where they might be found.

⁹ See also the fascinating N-body experiments of Holmberg (1941) in which gravitational forces were calculated using light bulbs and photocells. Back.