6.3. Angular momentum

One of the consequences of gravitational instability is that individual proto-structures would have been set in rotation by the tidal torques from their neighbours. Hoyle (1949) was the first to suggest that this mechanism might account for the rotation of galaxies and the idea was refined further by Peebles (1969). Peebles used the linear theory (Section 5.1) to make an estimate of the angular momentum acquired by a protogalaxy and we shall follow his approach below.

The angular momentum about the centre of a sphere of volume may be written

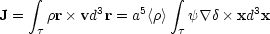(6.13)

where v = a . The origin of the coordinates is taken to be at the centre of the sphere and the notation throughout this section follows that of Section 5.1. In the linear theory, the Fourier transforms of the velocity potential and the fractional density contrast are given by Eqs. (5.7). On retaining only the growing modes,

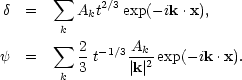(6.14a) (6.14b)

Rather than take the volume to be a sphere of radius x₀, it proves convenient to weight the volume by a factor exp[|x - x'| / x₀²]. In this case, Eqs. (6.13) and (6.14) give,

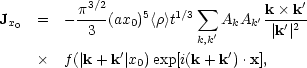(6.15)

where f (y) = exp(- y²/4).

Equation (6.15) may be corrected for the translational motion of the centre of mass of the volume. The angular momentum about the centre of mass is then,

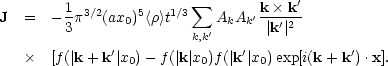(6.16)

Thus, the angular momentum grows at t^5/3 in an = 1 universe. The mean square density contrast within a typical volume is,

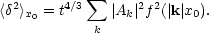(6.17)

Hence the root mean square angular momentum may be written,

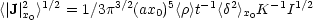(6.18)

where we have taken,

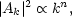(6.19a)

and the integrals K and I are,

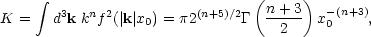(6.19b)

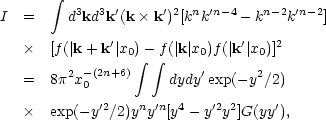(6.19c)

where

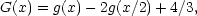and

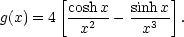The integral I diverges if n lies outside the range -3 < n < 1/2. For intermediate values, the combination I^1/2 K^-1 has been evaluated numerically and is listed below.

n	0.45	0.25	0.00	-0.25	-0.50	-1.00	-2.00
I1/2 K-1	3.19	1.35	0.89	0.68	0.55	0.39	0.21

If n > 1/2, the dominant contribution to the integral I occurs at short wavelengths where the power spectrum breaks away from its primordial shape due to non-linear effects.

From Eq. (6.18),

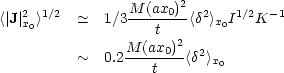(6.20)

(cf. Peebles, 1969, Eq. 24).

Most of the angular momentum is acquired during the linear regime; in the non-linear regime galaxies recede from each other, their separations increasing as t^2/3. The torque on any galaxy therefore decreases as 1/t². A rough estimate of the angular momentum may, therefore, be obtained from Eq. (6.20) by setting <²>_x0 1. In terms of the dimensionless spin-parameter defined by Eq. (6.10) we find,

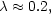(6.21)

for a typical protogalaxy. In deriving Eq. (6.21) we have taken n 0. As may be seen from the table above, the angular momentum is fairly insensitive to the value of n for the range -1 n 0 which we have argued in Section (5.3) is required if the theory is to account for the observations of the two-point galaxy correlation function. This answer must be considered fairly rough as it gives the r.m.s. angular momentum of a randomly placed sphere whereas what is really wanted is the angular momentum of a bound protogalaxy. Also the extrapolation of Eq. (6.20) to density contrasts <²>_x0 ~ 1 is somewhat uncertain. A more accurate estimate may be obtained from N-body calculations (Peebles, 1971b; Efstathiou and Jones, 1979). In particular, the latter authors studied the tidal torque process using 1000 particle models with Poisson initial conditions. For bound clumps, with density contrast 10, they find the median value of to be,

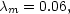(6.22)

with no significant dependence on the mass of the clump.

For a spheroidal galaxy with a Hubble-like density profile and a flat rotation curve, the spin parameter is approximately 0.33v_m / ₀, where v_m and ₀ are the projected rotational velocity and central velocity dispersion respectively when the galaxy is viewed along the equatorial plane (White (1979a)). Correcting this by a factor of /4 to account for the random orientations of galaxies in space, Eq. (6.22) predicts (v_m / ₀)_median 0.14. This result is fairly typical of bright elliptical galaxies with M_B < - 20 (Section 2.1). Fainter ellipticals rotate more rapidly, with v_m / ₀ 0.2. This may not be a problem for the tidal torque theory since the spin-parameter is only conserved if total energy is conserved during the collapse; it may be that the fainter elliptical galaxies increased their binding energy in a dissipative collapse whilst the larger ones did not. This idea will be discussed further in Section 8.2.

The theory does, however, face a serious problem in accounting for the rotation of disc galaxies if they formed from the collapse of self-gravitating gas clouds. Consider a self-gravitating exponential disc (Section 2.2). In the absence of random motions, the total angular momentum is,

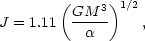(6.23)

and the total energy is,

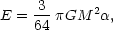(6.24)

where ^-1 is the scale length of the disc. A disc galaxy, therefore, has a spin-parameter,

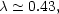(6.25)

which is far in excess of the tidal torque prediction (6.22). It is quite clear that dissipative processes have played a major role in the formation of disc systems so we would expect angular momentum but not energy to be conserved during the collapse. We may therefore use Eqs. (6.22) and (6.23) to estimate the initial radius of the protocloud at time t_i when / ~ 1. Approximating the protocloud as a uniform sphere of radius R_i and total energy E_i = 3/5 GM² / Rⁱ, the spin-parameter at time t_i is _i 0.86( R_i)^-1/2 since angular momentum is conserved during the collapse. Equating _i with Eq. (6.23) we find,

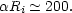(6.26)

Hence a typical disc galaxy with scale length ^-1 3h^-1 kpc must have collapsed from a protocloud with R_i 600h^-1 kpc. For a mass of 10¹¹ M this implies a free-fall time of,

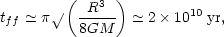(6.27)

which is greater than the age of the Universe. Clearly, the collapse factor of Eq. (6.26) is unreasonably large; a more acceptable value would be R_i 10 (Eggen, Lynden-Bell and Sandage, 1962). A possible resolution of this problem will be discussed in Section 8.2.

It is also interesting to examine the nature of the tidally induced velocity field. From Eq. 5.3(b) we find,

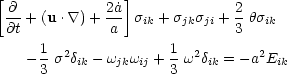(6.28)

where

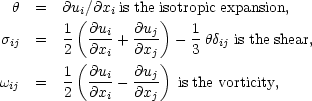and

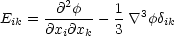is the tidal field. Now, if the vorticity is assumed to be zero at recombination it will remain so at any later time since Kelvin's circulation theorem holds,

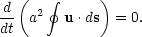Thus, in the linear regime, Eq. (6.28) may be solved giving,

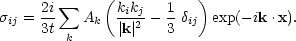(6.29)

The root mean square value of the shear within a randomly placed sphere of radius x₀ is,

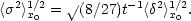(6.30)

The effect of shear is to elongate the perturbation. The ellipticity will be of order t. Hence, Eq. (6.30) shows that the distortion will grow as t^2/3 and is of first order in the amplitude (cf. Binney and Silk (1979)). By the time that 1 quite significant elongations could be produced, with ~ 1/2.