3.3. Superconducting strings !

One of the most amazing things of the strings we are now treating is the fact that, provided some general conditions (e.g., the appropriate relation between the free parameters of the model) are satisfied, these objects can turn into superconductors. So, under the conditions that the e A^µ term dominates in the expression for the current 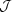^z, we can write

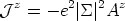
(26)

which is no other than the London equation [London & London, 1935]. From it, recalling the Faraday's law of the set of Maxwell equations, we can take derivatives on both sides to get

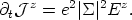
(27)

Then, the current grows up linearly in time with an amplitude proportional to the electric field. This behavior is exactly the one we would expect for a superconductor [Tinkham, 1995]. In particular, the equation signals the existence of persistent currents. To see it, just compare with the corresponding equation for a wire of finite conductivity 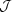^z = E^z. One clearly sees in this equation that when the applied electric field is turned off, after a certain characteristic time, the current stops. On the contrary, in Eq. (27), when the electric field vanishes, the current does not stop but stays constant, i.e., it persists flowing along the string.

At sufficiently low temperatures certain materials undergo a phase transition to a new (superconducting) phase, characterized notably by the absence of resistance to the passage of currents. Unlike in these theories, no critical temperature is invoked in here, except for the temperature at which the condensate forms inside the string, the details of the phase transition being of secondary importance. Moreover, no gap in the excitation spectrum is present, unlike in the solid-state case where the amount of energy required to excite the system is of the order of that to form a Cooper pair, and hence the existence of the gap.

The very same considerations of the above paragraphs are valid for fermion (massless) zero modes along the string [Witten, 1985]. In fact, a generic prediction of these models is the existence of a maximum current above which the current-carrying ability of the string saturates. In his pioneering paper, Witten pointed out that for a fermion of charge q and mass in vacuum m, its Fermi momentum along the string should be below its mass (in natural units). If this were not the case, i.e., if the momenta of the fermions exceeded this maximum value, then it would be energetically favorable for the particle to jump out of the core of the string [Gangui et al., 1999]. This implies that the current saturates and reaches a maximum value

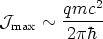
(28)

If we take electrons as the charge carriers, then one gets currents of size 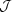_max ~ tens of ampères, interesting but nothing exceptional (standard superconducting materials at low temperature reach thousands of ampères and more). On the other hand, if we focus in the early universe and consider that the current is carried by GUT superheavy fermions, whose normal mass would be around 10¹⁶ GeV, then currents more like 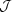_max ~ 10²⁰ A are predicted. Needless to say, these currents are enormous, even by astrophysical standards!

Und Meissner ..? It has long been known that superconductors exclude static magnetic fields from their interior. This is an effect called the Meissner effect, known since the 1930s and that was later explained by the BCS (or Bardeen-Cooper-Schrieffer) theory in 1957. One can well wonder what the situation is in our present case, i.e., do current-carrying cosmic strings show this kind of behavior?

To answer this question, let us write Ampère's law (in the Coulomb, or radiation, gauge 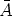^. = 0)

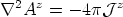
(29)

Also, let us rewrite the London equation

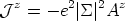
(30)

Putting these two equations together we find

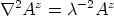
(31)

where we wrote the electromagnetic penetration depth ~ (e|(0)|)^-1.

Roughly, for Cartesian coordinates, if we take 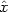perpendicular to the surface, we have A^z e^-x/, which is nothing but the expected exponential decrease of the vector potential inside the core [Meissner, 1933]. [to be more precise, in the string case we expect ² P_a = e² ||² P_a, with P_a = _a + e A_a].

For a lump of standard metal a penetration depth of roughly ~ 10^-5cm is ok. In the string case, however,

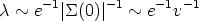
(32)

which is roughly the Compton wavelength of A_µ. Now, recall that we had v^-1 > ^-1, and that ^-1 was the characteristic (Compton) size of the string core. Hence we finally get that can be bigger than the size of the string - unlike what happens with standard condensed-matter superconductors, electromagnetic fields can penetrate the string core!