


5.2. CMB bispectrum from active models
Different cosmological models differ in their predictions for the statistical distribution of the anisotropies beyond the power spectrum. Future MAP and Planck satellite missions will provide high-precision data allowing definite estimates of non-Gaussian signals in the CMB. It is therefore important to know precisely which are the predictions of all candidate models for the statistical quantities that will be extracted from the new data and identify their specific signatures.
Of the available non-Gaussian statistics, the CMB bispectrum, or the three-point function of Fourier components of the temperature anisotropy, has been perhaps the one best studied in the literature [Gangui & Martin, 2000a]. There are a few cases where the bispectrum may be deduced analytically from the underlying model. The bispectrum can be estimated from simulated CMB sky maps; however, computing a large number of full-sky maps resulting from defects is a much more demanding task. Recently, a precise numerical code to compute it, not using CMB maps and similar to the CMBFAST code (17) for the power spectrum, was developed in [Gangui, Pogosian & Winitzki 2001b]. What follows below is an account of this work.
In a few words, given a suitable model, one can generate a statistical ensemble of realizations of defect matter perturbations. We used a modified Boltzmann code based on CMBFAST to compute the effect of these perturbations on the CMB and found the bispectrum estimator for a given realization of sources. We then performed statistical averaging over the ensemble of realizations to compute the expected CMB bispectrum. (The CMB power spectrum was also obtained as a byproduct.) As a first application, we then computed the expected CMB bispectrum from a model of simulated string networks first introduced by Albrecht et al. [1997] and further developed in [Pogosian & Vachaspati, 1999] and in [Gangui, Pogosian & Winitzki 2001].
We assume that, given a model of active perturbations, such as a
string simulation, we can calculate the energy-momentum tensor
Tµ (x,
(x,
 ) for a particular
realization of the sources in a finite spatial
volume V0. Here, x is a 3-dimensional
coordinate and
) for a particular
realization of the sources in a finite spatial
volume V0. Here, x is a 3-dimensional
coordinate and  is the
cosmic time. Many simulations are run to obtain an ensemble of random
realizations of sources with statistical properties appropriate for
the given model. The spatial Fourier decomposition
of Tµ
is the
cosmic time. Many simulations are run to obtain an ensemble of random
realizations of sources with statistical properties appropriate for
the given model. The spatial Fourier decomposition
of Tµ can be written as
can be written as

| (85) |
where k are discrete. If V0 is sufficiently large we can approximate the summation by the integral

| (86) |
and the corresponding inverse Fourier transform will be

| (87) |
Of course, the final results, such as the CMB power spectrum or bispectrum, do not depend on the choice of V0. To ensure this independence, we shall keep V0 in all expressions where it appears below.
It is conventional to expand the temperature fluctuations over the basis of spherical harmonics,

| (88) |
where 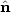 is a
unit vector. The coefficients alm can be
decomposed into Fourier modes,
is a
unit vector. The coefficients alm can be
decomposed into Fourier modes,

| (89) |
Given the sources  µ
µ (k,
(k,
 ), the quantities
), the quantities
 l(k)
are found by solving linearized
Einstein-Boltzmann equations and integrating along the line of sight,
using a code similar to CMBFAST
[Seljak & Zaldarriaga,
1996].
This standard procedure can be written
symbolically as the action of a linear operator
l(k)
are found by solving linearized
Einstein-Boltzmann equations and integrating along the line of sight,
using a code similar to CMBFAST
[Seljak & Zaldarriaga,
1996].
This standard procedure can be written
symbolically as the action of a linear operator
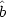 lµ
lµ (k)
on the source energy-momentum tensor,
(k)
on the source energy-momentum tensor,
 l(k)
=
l(k)
= 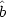 lµ
lµ (k)
(k)
 µ
µ (k,
(k,
 ),
so the third moment of
),
so the third moment of
 l(k)
is linearly related to the three-point correlator of
l(k)
is linearly related to the three-point correlator of
 µ
µ (k,
(k,
 ). Below
we consider the quantities
). Below
we consider the quantities
 l(k),
corresponding to a
set of realizations of active sources, as given. The numerical
procedure for computing
l(k),
corresponding to a
set of realizations of active sources, as given. The numerical
procedure for computing
 l(k)
was developed in
[Albrecht et al. 1997]
and in
[Pogosian & Vachaspati,
1999].
l(k)
was developed in
[Albrecht et al. 1997]
and in
[Pogosian & Vachaspati,
1999].
The third moment of alm, namely <al1 m1 al2 m2 al3 m3> , can be expressed as

| (90) |
A straightforward numerical evaluation of Eq. (90) from given sources
 l(k)
is prohibitively difficult, because it involves too many integrations of
oscillating functions. However, we shall be able to reduce the
computation to integrations over scalars [a similar method was
employed in
Komatsu & Spergel,
2001
and in
Wang & Kamionkowski,
2000].
Due to homogeneity, the 3-point function vanishes unless the triangle
constraint is satisfied,
l(k)
is prohibitively difficult, because it involves too many integrations of
oscillating functions. However, we shall be able to reduce the
computation to integrations over scalars [a similar method was
employed in
Komatsu & Spergel,
2001
and in
Wang & Kamionkowski,
2000].
Due to homogeneity, the 3-point function vanishes unless the triangle
constraint is satisfied,

| (91) |
We may write

| (92) |
where the three-point function
Pl1l2l3(k1,
k2, k3) is defined only
for values of ki that satisfy
Eq. (91). Given the scalar values k1,
k2, k3, there is a unique (up to an
overall rotation) triplet of directions
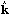 i for
which the RHS of Eq. (92) does not vanish. The quantity
Pl1l2l3(k1,
k2, k3) is invariant under an overall
rotation of all three vectors ki and therefore may be
equivalently represented by a function of scalar values
k1, k2, k3, while
preserving all angular
information. Hence, we can rewrite Eq. (92) as
i for
which the RHS of Eq. (92) does not vanish. The quantity
Pl1l2l3(k1,
k2, k3) is invariant under an overall
rotation of all three vectors ki and therefore may be
equivalently represented by a function of scalar values
k1, k2, k3, while
preserving all angular
information. Hence, we can rewrite Eq. (92) as

| (93) |
Then, using the simulation volume V0 explicitly, we have

| (94) |
Given an arbitrary direction
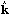 1 and the
magnitudes
k1, k2 and k3, the
directions
1 and the
magnitudes
k1, k2 and k3, the
directions
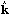 2
and
2
and 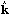 3
are specified up to overall rotations by the
triangle constraint. Therefore, both sides of Eq. (94) are
functions of scalar ki only. The expression on the RHS
of Eq. (94) is evaluated numerically by averaging over different
realizations of the sources and over permissible directions
3
are specified up to overall rotations by the
triangle constraint. Therefore, both sides of Eq. (94) are
functions of scalar ki only. The expression on the RHS
of Eq. (94) is evaluated numerically by averaging over different
realizations of the sources and over permissible directions
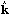 i;
below we shall give more details of the procedure.
i;
below we shall give more details of the procedure.
Substituting Eqs. (93) and (94) into (90), Fourier transforming the Dirac delta and using the Rayleigh identity, we can perform all angular integrations analytically and obtain a compact form for the third moment,

| (95) |
where, denoting the Wigner 3j-symbol by
 ,
we have
,
we have
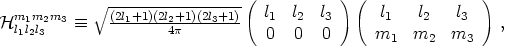
| (96) |
and where we have defined the auxiliary quantities bl1l2l3 using spherical Bessel functions jl,

| (97) |
The volume factor V03 contained in this
expression is correct: as shown in the next section, each term
 l
includes a factor
V0-2/3, while the average quantity
Pl1l2l3(k1,
k2, k3)
l
includes a factor
V0-2/3, while the average quantity
Pl1l2l3(k1,
k2, k3)
 V0-3
[cf. Eq. (94)], so that the arbitrary volume V0 of
the simulation cancels.
V0-3
[cf. Eq. (94)], so that the arbitrary volume V0 of
the simulation cancels.
Our proposed numerical procedure therefore consists of computing the
RHS of Eq. (95) by evaluating the necessary integrals. For fixed
{l1l2l3} ,
computation of the quantities
bl1l2l3(r)
is a triple integral over scalar ki defined
by Eq. (97); it is followed by a fourth
scalar integral over r [Eq. (95)]. We also need to average over
many realizations of sources to obtain
Pl1l2l3
(k1,k2,k3) .
It was not feasible for us to precompute the
values
Pl1l2l3
(k1, k2, k3) on a
grid
before integration because of the large volume of data: for each set
{l1l2l3} the grid
must contain ~ 103
points for each ki. Instead, we precompute
 l
(k) from one realization of sources and evaluate the RHS
of Eq. (94) on that data as an estimator of
Pl1l2l3
(k1,k2,k3) ,
averaging over allowed directions of
l
(k) from one realization of sources and evaluate the RHS
of Eq. (94) on that data as an estimator of
Pl1l2l3
(k1,k2,k3) ,
averaging over allowed directions of
 i. The result is used for
integration in Eq. (97).
i. The result is used for
integration in Eq. (97).
Because of isotropy and since the allowed sets of directions
 i are
planar, it is enough
to restrict the numerical calculation to directions
i are
planar, it is enough
to restrict the numerical calculation to directions
 i
within a fixed two-dimensional plane. This significantly reduces the
amount of computations and data storage, since
i
within a fixed two-dimensional plane. This significantly reduces the
amount of computations and data storage, since
 l
(k) only needs to be stored on a two-dimensional grid of k.
l
(k) only needs to be stored on a two-dimensional grid of k.
In estimating
Pl1l2l3
(k1, k2, k3)
from Eq. (94), averaging over directions of
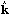 i
plays a similar role to ensemble averaging over source
realizations. Therefore if the number of directions is large enough
(we used 720 for cosmic strings), only a moderate number of different
source realizations is needed. The main numerical difficulty is the
highly oscillating nature of the function
bl1l2l3(r).
The calculation of the bispectrum for cosmic
strings presented in the next Section requires about 20 days of a
single-CPU workstation time per realization.
i
plays a similar role to ensemble averaging over source
realizations. Therefore if the number of directions is large enough
(we used 720 for cosmic strings), only a moderate number of different
source realizations is needed. The main numerical difficulty is the
highly oscillating nature of the function
bl1l2l3(r).
The calculation of the bispectrum for cosmic
strings presented in the next Section requires about 20 days of a
single-CPU workstation time per realization.
We note that this method is specific for the bispectrum and cannot be applied to compute higher-order correlations. The reason is that higher-order correlations involve configurations of vectors ki that are not described by scalar values ki and not restricted to a plane. For instance, a computation of a 4-point function would involve integration of highly oscillating functions over four vectors ki which is computationally infeasible.
From Eq. (95) we derive the CMB angular bispectrum
 l1l2l3, defined
as [Gangui & Martin,
2000b]
l1l2l3, defined
as [Gangui & Martin,
2000b]

| (98) |
The presence of the 3 j-symbol guarantees that the third moment
vanishes
unless m1 + m2 +
m3 = 0 and the li indices satisfy the
triangle
rule |li - lj|
 lk
lk
 li +
lj. Invariance under spatial
inversions of the three-point correlation function implies the additional
`selection rule' l1 + l2 +
l3 = even, in order for the third
moment not to vanish. Finally, from this last relation and
using standard properties of the 3 j-symbols, it follows that the
angular bispectrum
li +
lj. Invariance under spatial
inversions of the three-point correlation function implies the additional
`selection rule' l1 + l2 +
l3 = even, in order for the third
moment not to vanish. Finally, from this last relation and
using standard properties of the 3 j-symbols, it follows that the
angular bispectrum  l1l2l3
is left unchanged
under any arbitrary permutation of the indices li.
l1l2l3
is left unchanged
under any arbitrary permutation of the indices li.
In what follows we will restrict our calculations to the angular bispectrum Cl1l2l3 in the `diagonal' case, i.e. l1 = l2 = l3 = l. This is a representative case and, in fact, the one most frequently considered in the literature. Plots of the power spectrum are usually done in terms of l(l + 1)Cl which, apart from constant factors, is the contribution to the mean squared anisotropy of temperature fluctuations per unit logarithmic interval of l. In full analogy with this, the relevant quantity to work with in the case of the bispectrum is

| (99) |
For large values of the multipole index l,
Glll
 l3/2 Clll. Note also what
happens with the 3 j-symbols
appearing in the definition of the coefficients
l3/2 Clll. Note also what
happens with the 3 j-symbols
appearing in the definition of the coefficients
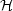 l1l2l3m1m2m3:
the symbol
l1l2l3m1m2m3:
the symbol
 is absent from the definition of
Cl1l2l3,
while in Eq. (99) the symbol
is absent from the definition of
Cl1l2l3,
while in Eq. (99) the symbol
 is squared. Hence, there are no remnant oscillations due
to the alternating sign of
is squared. Hence, there are no remnant oscillations due
to the alternating sign of
 .
.
However, even more important than the value of Clll itself is the relation between the bispectrum and the cosmic variance associated with it. In fact, it is their comparison that tells us about the observability `in principle' of the non-Gaussian signal. The cosmic variance constitutes a theoretical uncertainty for all observable quantities and comes about due to the fact of having just one realization of the stochastic process, in our case, the CMB sky [Scaramella & Vittorio, 1991].
The way to proceed is to employ an estimator
 l1l2l3
for the bispectrum and compute the
variance from it. By choosing an unbiased estimator we ensure it satisfies
Cl1l2l3
= <
l1l2l3
for the bispectrum and compute the
variance from it. By choosing an unbiased estimator we ensure it satisfies
Cl1l2l3
= < l1l2l3>.
However, this condition does not
isolate a unique estimator. The proper way to select the best
unbiased estimator is to compute the variances of all candidates and
choose the one with the smallest value. The estimator with this
property was computed in
[Gangui & Martin,
2000b]
and is
l1l2l3>.
However, this condition does not
isolate a unique estimator. The proper way to select the best
unbiased estimator is to compute the variances of all candidates and
choose the one with the smallest value. The estimator with this
property was computed in
[Gangui & Martin,
2000b]
and is

| (100) |
The variance of this estimator, assuming a mildly non-Gaussian distribution, can be expressed in terms of the angular power spectrum Cl as follows
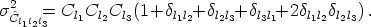
| (101) |
The theoretical signal-to-noise ratio for the bispectrum is then given by

| (102) |
In turn, for the diagonal case l1 = l2 = l3 = l we have

| (103) |
Incorporating all the specifics of the particular experiment, such as sky coverage, angular resolution, etc., will allow us to give an estimate of the particular non-Gaussian signature associated with a given active source and, if observable, indicate the appropriate range of multipole l's where it is best to look for it.
17 http://physics.nyu.edu/matiasz/CMBFAST/cmbfast.html Back.