6.3. The Energy Budget of the BLR

While the individual line ratios are the best indicators for the physical conditions in the BLR clouds, a simple energy conservation argument provides another strong constraint on the models.

Consider optically thick clouds absorbing only ionizing radiation, and no reddening by dust. The total energy emitted by the clouds is simply the energy absorbed by them, which is the product of the ionizing radiation and the covering factor. Photoionization calculations for the BLR indicate that the emitted L flux is not very different from the "Case B flux" mentioned earlier, whereby each absorbed ionizing photon results in one L** photon. In this case the number of L photons is the product of the number of ionizing photons and the covering factor. Combining the two we have a simple observational way to measure the mean energy of an ionizing photon, (in Ryd.):

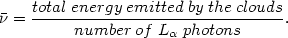
(63)

This is a most important information about the shape of the Lyman continuum that cannot be obtained by direct observations of the Lyman continuum.

The integrated flux emitted by the BLR clouds is not easy to measure since some of it is in broad spectral features, such as the "small 2000-4000Å bump", the Paschen continuum and several infrared lines. It is estimated to be 5-9 times the L intensity which means, according to the above relation, 4 - 7 Ryd.

To illustrate this further assume that the ionizing continuum is a simple power-law in energy, L = C^-, extending up to a cut-off frequency _cut, where is in Rydberg and C is a constant. The mean energy of an ionizing photon is

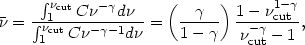
(64)

where we have assumed 1,0. This expression should be compared with (63) to obtain the value of . For example, for _cut = 10 Ryd, which is consistent with the observational constraints mentioned in chapter 4, we get 0. This is in conflict with the observations that show a typical observed slope, at a rest wavelength of 1000Å, of about = 0.6 and an even steeper slope at shorter wavelengths. The discrepancy has been named "the energy budget problem".

There are several suggested solutions to this problem. First, only the soft ( 10 Ryd) Lyman continuum photons have been considered here while high energy photons are observed in almost all AGNs. Such photons hardly interact with the gas unless the column density is much greater than 10²³ cm^-2. Very thick clouds have been suggested, in which a large fraction of the high energy continuum is absorbed by the gas. Thick clouds can also absorb the infrared continuum, which helps too. Second, the models may be wrong, in particular the assumption about the number of L photons and its relation to the ionizing flux. Also, the observed lines may come from two distinct parts of the BLR (the surface of the central disk?). Third, the above argument makes use of the intrinsic properties of AGNs, but the observed fluxes may be different from the intrinsic fluxes. For example, reddening by dust can change the observed line ratio and the inferred mean photon energy. None of these explanations is entirely satisfactory and it is likely that the real solution involves some combination of all.

A somewhat related problem is the ratio of the high and low excitation lines. Generally speaking, much of the "soft" ionizing flux ( 20 Ryd.) is converted to recombination and high ionization lines, while the harder photons, that can penetrate much deeper, are converted to low excitation lines. It can thus be argued that the flux ratio of high to low ionization lines is a measure of the flux at different wavelengths. One can use it to formulate a "second order energy budget problem" related to the fact that the observed low excitation lines of MgII and FeII are too strong relative to H. This cannot be solved by reddening but the argument is based, to a large extent, on the observed FeII lines, that are not well understood.

There are other methods for estimating the shape of the ionizing continuum. In particular, the equivalent width (EW) of the recombination lines can be used for that. For example, the "Case B" L equivalent width, for a system of optically thick clouds with a covering factor C(r), around the above power-law continuum, is:

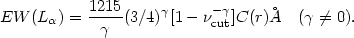
(65)

A similar ratio can be calculated for EW(HeII1640), where the integration in this case is for 4Ryd. The observed EW of these two lines can be compared with this theoretical prediction in order to estimate the continuum slope around 1-4 Ryd. Alternatively, the EW of the HeII lines, combined with an assumption on the covering factor, can be used to estimate L(1640Å) / L(228Å) etc. These arguments cannot be simply used in the disk-like geometry mentioned in chapter 5.