1.2. Thermal Beginning of the Universe

The early universe, where very high densities and temperatures dominate, can be treated by using fluid thermodynamics. At very high temperatures, radiation and matter are in thermal equilibrium, coupled via Thomson scattering with the photons dominating over the nucleons (n / n_p 10⁹). Therefore the primordial fluid can be treated as radiation-dominated with p = 1 / 3 c² = 1 / 3 T⁴ and from (10), we obtain:

(11)

Therefore the temperature of the Universe drops linearly with the expansion scale factor. Furthermore, it is evident from (10), that the radiation density drops faster than the mass density and since we know from measurements that the universe is matter dominated today, then at some epoch in the past, say at a redshift z_eq, we had _m = _rad. It is easy to show that _r = _m R₀ / R_eq = (1 + z_eq) _m (the subscript 0 denotes the present epoch) and using the measured values of _i we have that:

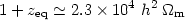
Therefore the thermal history of the Universe can be divided in two main eras: a radiation dominated era (z >> z_eq) and a matter dominated era (z << z_eq). In the radiation dominated era, in which we can neglect the curvature and terms in Friedmann's equation (see next section), we have:

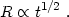
By differentiating this relation with respect to time and using (7) we have:

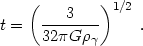
(12)

Using = ² k_b t⁴ / 15h³ c⁵ we finally obtain the important relation between cosmic time and the temperature of the Universe in the radiation dominated era:

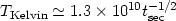
(13)

from which it is evident that the Universe at early times was hot enough for nucleosynthesis to occur, as it had been supposed originally by Gamow. The era of nucleosynthesis takes place around ~ 10⁹ K.

The Cosmic Microwave Background: Although the dynamics during the radiation dominated era are unaffected by ordinary matter, the electrons act as a scattering medium of the radiation and thus the Universe at this epoch is opaque. As the Universe cools, R^-1, electrons bind electrostatically with protons to form Neutral Hydrogen. Using Saha's ionization equation one finds that the temperature at which the number of free electrons drops significantly is t 3000 K.

Therefore when the universe cools at this temperature, the scattering medium disappears and the radiation freely escapes without being absorbed or scattered which means that the Universe becomes transparent. This epoch is called the recombination epoch.

The existence of the relics of this radiation was predicted by Gamow and his collaborators in the 1940s. It was subsequently discovered by Penzias & Wilson in 1965, while the whole spectrum of this radiation was traced to unprecedented accuracy by the COBE satellite observations. The CMB possesses a perfect black-body spectrum with a mean temperature of T₀ = 2.728 ± 0.004 K and it is extremely isotropic except for a dipole, which is however a local kinematical effect (due to our motion with respect to the cosmic rest frame defined by the CMB). From what redshift does the CMB radiation originate? From (11) we have that:

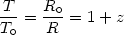
with T 3000 K and T₀ 2.73 we get that

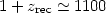
From (7) and (10) we have that in the matter dominated era R(t) t^2/3 and thus z_rec corresponds to a time:

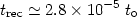
where t₀ is the present age of the Universe. Therefore by studying the microwave background sky we have direct information from the Universe when it was as young as t_rec.

The CMB dipole anisotropy: Due to our motion with respect to the isotropic CMB radiation we observe a dipole in the distribution of the radiation temperature. Although this has the appearance of a Doppler effect, in reality four different effects add up to produce this dipole seen by an observer moving with a velocity u. These four effects are:

• a Doppler effect that increases the frequency of photons, and thus the observed energy, seen in the direction of motion by a Doppler factor D 1 + (u/c) cos
• the interval of frequencies increases by the same factor in the direction of motion, and therefore since T E / , the above two effects cancel out.
• the moving observer selects in the direction of motion relatively more photons by a factor D
• the solid angle in the direction of motion is smaller by a factor D^-2 due to abberation.

The net effect is that the moving observer sees an intensity of CMB radiation I_mov = (1 + u/c cos )³ I_rest. Due to the adiabatic expansion of the Universe, (t R^-1), the shape of the Planck spectrum:

should be preserved, which then necessarily implies that T () = (1 + u/c cos ) T₀ and thus:

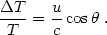
(14)

COBE observed a CMB dipole amplitude of T ~ 3.3(±0.2) mK (which corresponds to a fluctuation T / T = 1.2(±0.03) × 10^-3). The corresponding velocity of Earth is:

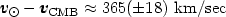
towards the galactic coordinates (l, b) = (265°, 48°) (see [159]). This motion is due to the vectorial sum of the motion of the Earth around the Sun, of the Sun within the Galaxy, of the Galaxy within the Local Group and of the peculiar motion of the Local Group, due to the gravitational effects of large-scale density fluctuations. The motion of the Earth with respect to the LG centroid is:

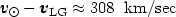
towards (l, b) = (107°, -7°) and thus we find the velocity of the LG centroid with respect to the CMB:

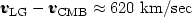
towards (l, b) = (277°, 30°) .

The Local Group velocity was originally thought as the result of the attraction of the Local Supercluster (Virgo). However, there is a residual velocity of ~ 400 km/sec that must be due to gravitational forces acting on the LG from distances greater than the Local Supercluster's centre-of-mass (cz ~ 1100 km/sec). Many earlier studies pointed towards the ‘Great Attractor', a mass concentration of ~ 5 × 10¹⁶ M located at a distance of 42 h^-1 Mpc and at low Galactic latitudes, as being the sole cause of a relatively local coherent motion, in which the Local Group partakes (cf. [94], [93]). Later studies, indicated that another very massive and more distant (~ 140 h^-1 Mpc) attractor could play a significant role in shaping the local dynamics ([151], [152], [122]). It seems that the coherence scale of the velocity field could extend to even larger distances than what originally thought (cf. [11], however for a different view see [40]).