1.3. Cosmological Parameters

Based on (7) we can define some very important parameters like the Critical Density, which is the density necessary to obtain a flat Universe ( = 0):

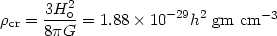
(15)

and the Cosmological density parameter , which is a unit-less measure of the density of the Universe:

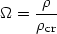
(16)

Furthermore, the constant of proportionality in Hubble's law, the Hubble constant, is:

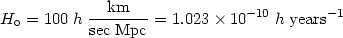
(17)

Note that the necessity of parametrizing with h was due to earlier discordant determinations of H₀. Today most studies converge to a value of ~ 0.7 (see section 2.4).

A convenient representation of these interrelations can be produced by re-writing Friedmann's equation, in the matter dominated era (using 10), as following:

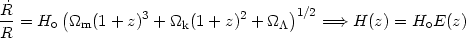
(18)

were the contribution to the total density parameter from the curvature and terms is:

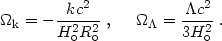
(19)

Note that H(z) is called Hubble function. It is evident that at the present epoch we obtain from (18) that E(0) = 1 and thus:

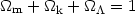
(20)

which also holds for any epoch (evaluated directly from 7). Note that we can have a flat Universe (_k = 0) while having _m < 1 (as suggested by many different observations).

The Age of the Universe: Using (18), evaluated at the present epoch, we have / R₀ = H₀ E(z) / (1 + z) and from dR/R₀ = -dz / (1 + z)² we obtain the age of the Universe:

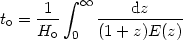
(21)

For example, in an Einstein-de Sitter universe ( = _k = 0) we have:

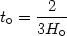
(22)

while for a > 0 model we obtain:

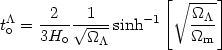
(23)

We therefore see that if > 0 we have that the age of the Universe is larger than what is predicted in an Einstein-de Sitter Universe.

The 0 Universe: Due to the recent exciting observational indications for a positive cosmological constant and the important consequences that this has to our understanding of the Cosmos, we will briefly present this model.

Originally, the cosmological -parameter was introduced ad hoc by Einstein in his field equations in order to get a static solution ( = = 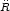0). From (8) he derived R = (k / _c)^1/2 and inserting this into (7) he obtained, in a matter dominated (p = 0) Universe:

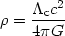
(24)

where _c is the critical value of for which = = 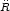0. However, it was found that his solution was unstable and that small perturbations of the value of _c would change drastically the behaviour of R. From (7) we see that if k 0, then ² is always nonnegative for > 0, and thus the universe expands for ever, while if < 0 then the universe can expand and then recontract again (as in the k = 1, = 0 case).

The recent SNIa observations (see section 3.2) and the CMB power-spectrum results (see section 3.1) have shown that the Standard Cosmological paradigm should be considered that of a flat, 0.7, _m 0.3 model. Thus we will consider such a model in the following discussion. Evaluating (7) at the present epoch, changing successively variables: x = R^3/2, y = x(_m / )^1/2 R₀^-3/2 and = sinh ^-1 y and then integrating, we obtain:

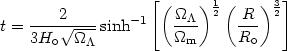
(25)

and

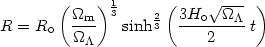
(26)

Figure 1. The expansion of the Universe in an Einstein de-Sitter (EdS) and in the preferred model. We indicate the inflection point beyond which the expansion accelerates. It is evident that in this model we live in the accelerated regime and thus the age of the Universe is larger than the Hubble time (H0-1).

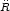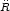It is interesting to note that in this model there is an epoch which corresponds to a value of R = R_I, where the expansion slows down and remains in a quasi-stationary phase for some time, expanding with > 0 thereafter (see Fig.1). At the quasi-stationary epoch, called the inflection point, we have = 0 and thus from (7) by differentiation we have:

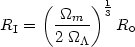
(27)

Now from (25) and (27) we have that the age of the universe at the inflection point is:

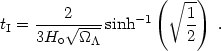
(28)

The Hubble function at t_I is:

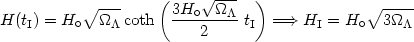
so if t₀ > t_I we must have H₀ < H_I.

This is an important result because it indicates that introducing an -term, and if we live at a time that fulfils the condition t₀ > t_I, we can increase the age of the universe to comfortably fit the globular cluster ages while keeping the value of _m < 1 and also a flat (_k = 0) space geometry. From (28) and (23) and for the preferred values = 0.7 and _m = 0.3 we indeed obtain t₀ / t_I 1.84 (see also Fig.1), which implies that we live in the accelerated phase of the Universe. Note that in order for the present time (t₀) to be in the accelerated phase of the expansion we must have: > 1/3.

Importance of k and terms in global dynamics: Due to the recent interest in the > 0, k = 0 Universes, it is important to investigate the dynamical effects that this term may have in the evolution of the Universe and thus also in the structure formation processes (see Fig.2). We realize these effects by inspecting the magnitudes of the two terms in the right hand side of (7). We have the density term:

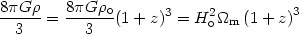
and from (20) we have

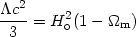
(29)

By equating the above two terms we can find the redshift at which they have equal contributions to the dynamics of the Universe. Evidently this happens only in the very recent past:

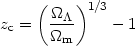
(30)

Observations suggest that _m 0.3 and 0.7, and therefore we have z_c 0.3, which implies that the present dynamics of the universe are dominated by the -term, although for the largest part of the history of the Universe the determining factor in shaping its dynamical evolution is the matter content.

Figure 2. The strength of the three factors shaping the recent dynamics of the Universe. Compare the strength of the and term (k = 0) and of the and k term. We have assumed H0 = 72 km s-1 Mpc-1, m = 0.3 and = 0.7.

Similar results are found for the k-term in = 0 models. In this case we have from (29) that

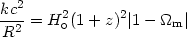
and thus the redshift at which the density and curvature terms have equal impact in the global dynamics, is:

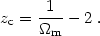
We see that as z increases the density term grows faster than the curvature term which is important only very recently. A similar line of argument shows that also in the radiation dominated era the and k terms do not affect the dynamics of the Universe.

Density parameter as a function of z: From (18) and eliminating the curvature term, using _k = 1 - _m - , we obtain the time evolution of the density parameter _m:

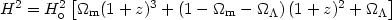
(31)

and using (15) and (10) we have:

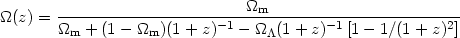
(32)

It is easy to see that whatever the value of _m, at large z we always have (z) = 1.