One of the most important parameters in determining the fate of the
Universe as a whole, is the present day expansion rate of the Universe,
which is encapsulated in the value of the Hubble constant
H0. Its
value sets the age of the Universe and specifies the value of the
critical density
cr,
and through this route the geometry of the Universe.
From the Hubble law (2) it is evident that in order to determine its
value we need to determine the expansion velocity (redshift) as
well as the distance of extragalactic objects, but within a redshift
such that space-curvature effects do not affect distances (43). A
further concern is that local gravitational effects produce peculiar
velocities, that are superimposed on the general expansion. This
can easily be seen in the toy model of (2), if we allow
(t). Then
|
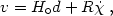
with the factor on the right being the peculiar velocity. Since the observer as well as the extragalactic object, of which the distance we want to measure, have peculiar velocities then the above equation becomes:
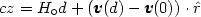
| (35) |
where v(0) is the velocity of the observer and
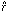is the unit vector along
the line-of-sight to the extragalactic object. It is then obvious that in
order to measure H0, the local velocity field should
be measured and the
extragalactic distances corrected accordingly. It is easily seen that if
both observer and galaxy take part in a coherent bulk flow, having the
same amplitude at the observer and galaxy positions, then the
right-hand part of (35) vanishes. In general however, one needs
good knowledge of the velocity field in order to correct distances
adequately.