


2.1. Distances of Extragalactic Objects
Our only means of obtaining information and therefore knowledge of the structure and dynamics of the Universe (on all different scales) are through the electromagnetic radiation that we receive. Therefore it is of primary importance to define a system of measuring luminosities taking also into account that the Universe expands and that light loses energy through a variety of processes.
If we assume that light propagates with no loss of energy, then the apparent luminosity of a source l, is related to its absolute luminosity L, by:

| (36) |
where r is the distance to the source. We can see the extreme importance of determining the pair (l, L), since such knowledge would provide the distance of the source, r.
Due to historical mostly reasons we use a logarithmic brightness system by which an object with a magnitude of 1 is 100 times brighter than an object with a magnitude 6. We have:

| (37) |
where m is the apparent magnitude and M the absolute one. Therefore, using (36) we have:

| (38) |
where c1,2 are constants which depend on the filter used and c3 is that value for which m = m at a distance of 10 parsecs (see section 2.3) from the Earth, and thus c3 = -5. In extragalactic astronomy, instead of pc, we use Mpc and therefore (38) becomes:

| (39) |
The above definitions are somewhat ideal, since in the real world we
do not observe the total apparent magnitude, but that corresponding to
the particular range of spectral frequencies, that our detector is sensitive
to, and those allowed to pass through Earth's atmosphere. If we detect
l over a range of frequencies
(
over a range of frequencies
( ±
±

 ), then the observed apparent
magnitude is m = -2.5 log10
), then the observed apparent
magnitude is m = -2.5 log10


 lsub>
lsub> d
d + c.
However, neither the atmosphere nor the detectors have a sharp
+ c.
However, neither the atmosphere nor the detectors have a sharp
 limit and therefore it is
better to model these effects by a sensitivity mask
F
limit and therefore it is
better to model these effects by a sensitivity mask
F , and the
observed apparent magnitude is then:
, and the
observed apparent magnitude is then:

| (40) |
If F = 1
then the apparent (or absolute) magnitude of a source is called
the bolometric magnitude.
= 1
then the apparent (or absolute) magnitude of a source is called
the bolometric magnitude.
How do the above definitions change by taking into account the fact
that the Universe expands? To answer this we need a metric of
space-time, which in our case is the Robertson-Walker
metric. Since light
travels along null-geodesics, a fundamental concept of distance can be
defined by the corresponding light-travel time, which is called
proper distance. If a light signal is emitted at a galaxy
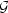 1 from the
coordinate position (r1,
1 from the
coordinate position (r1,
 0,
0,
 0) at time
t = 0 and received by an observer at
0) at time
t = 0 and received by an observer at
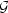 0 at
(r0,
0 at
(r0,
 0,
0,
 0), then these
events are connected only by the light signal and
since all observers must measure the same speed of light, it defines
a very fundamental concept of distance. Obviously, it depends
on the curvature of space, and since ds = 0 we have from (1):
0), then these
events are connected only by the light signal and
since all observers must measure the same speed of light, it defines
a very fundamental concept of distance. Obviously, it depends
on the curvature of space, and since ds = 0 we have from (1):

| (41) |
In the expanding Universe framework, the expressions (36) and (38) change, to:

| (42) |
where dL
 dpro(1 + z) is the luminosity
distance. It is obvious that the
distance measure of an extragalactic object depends on the underlying
Cosmology. A proper derivation of the luminosity distance (cf.
[183],
[112])
provides the following expression:
dpro(1 + z) is the luminosity
distance. It is obvious that the
distance measure of an extragalactic object depends on the underlying
Cosmology. A proper derivation of the luminosity distance (cf.
[183],
[112])
provides the following expression:

| (43) |
where  contains all
the contributions (mass, energy density, curvature).
Another important distance definition is that of the angular-diameter. It
is based on the fact that a length l, subtends a smaller angle,
contains all
the contributions (mass, energy density, curvature).
Another important distance definition is that of the angular-diameter. It
is based on the fact that a length l, subtends a smaller angle,
 ,
the further away it is (l
,
the further away it is (l
 1 /
1 /
 ) and it is given from:
relation to:
) and it is given from:
relation to:

| (44) |
Note that this notion of distance is used to derive the CMB power spectrum predictions of the different cosmological models (see section 3.1).