


2.2. Biases affecting Distance Determinations
Many effects, related either to our position in space (being on the plane of a dust-rich spiral galaxy), to natural limitations (introduced for example by the expansion of the Universe) or to detector related issues, introduce systematic biases that affect our ability to measure accurately distances. Below, I list a few of the most important such effects.
K-correction: Since bolometric magnitudes are not possible to measure, but rather magnitudes over a particular wavelength range, it is important to correct these magnitudes for the effect of the expansion of the Universe. These considerations result in modifying the distance modulus by a factor, the so-called K-correction factor:

| (45) |
This factor arises from the fact that when we measure the magnitude of
sources at large distances and at a particular frequency, say
 0,
we receive light emitted from a different part of the spectrum,
0,
we receive light emitted from a different part of the spectrum,
 e. It could well be
that in this latter part of the spectrum the
extragalactic object is particularly fainter or brighter than in the
nominal one,
e. It could well be
that in this latter part of the spectrum the
extragalactic object is particularly fainter or brighter than in the
nominal one,  0.
Furthermore, a combination of different factors;
evolution, intervening absorption processes or detector sensitivity
for example, result in energy losses as a function of wavelength,
which can be expressed by a mask
F(
0.
Furthermore, a combination of different factors;
evolution, intervening absorption processes or detector sensitivity
for example, result in energy losses as a function of wavelength,
which can be expressed by a mask
F( 0)
(40). Knowing
F(
0)
(40). Knowing
F( 0) one
can estimate the K-factor by integrating the spectrum at the
source rest frame. For example, such calculations have shown that a
typical value for spiral galaxies at z = 1 is K
0) one
can estimate the K-factor by integrating the spectrum at the
source rest frame. For example, such calculations have shown that a
typical value for spiral galaxies at z = 1 is K
 2 (in general
K(z)
2 (in general
K(z)  z).
z).
Malmquist bias: Due to the nature of
astronomical observation
there is a minimum flux density above which we select extragalactic
objects. As we look deeper in the Universe we tend to pick up a
relatively larger fraction of intrinsically bright objects (ie., only the
brighter end of the luminosity function is sampled). This bias arises
when determining distances from apparent magnitude limited
samples. If the individual absolute magnitudes
Mi of a sample of
extragalactic objects have a Gaussian distribution around
<M> with
dispersion  , then this
bias, for the case where the distribution
of extragalactic objects is considered homogeneous, is given by:
, then this
bias, for the case where the distribution
of extragalactic objects is considered homogeneous, is given by:

| (46) |
How does this bias affect the determination of extragalactic distances? The inferred distances of extragalactic objects are typically smaller than their true distances. From (39) we have that:

|
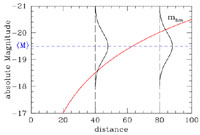
We illustrate this bias in Fig.4; as the
distance increases, M(mlim)
becomes brighter and therefore the brighter end of the luminosity
function is sampled. For a larger mlim (deeper sample)
the value of
M(mlim) increases (less luminous) so we have a
smaller  (M).
Conversely, for a given mlim and <M>, the
bias increases with distance.
(M).
Conversely, for a given mlim and <M>, the
bias increases with distance.
|
Figure 4. Illustration of Malmquist bias: Only objects with M above the mlim limit can be observed. At different distances different portions of the distribution around <M> can be observed. |
Note that we have considered a fairly straight-forward case, ie. that of a sample with a unique <M> value. In real samples of extragalactic objects we have a range of such values and therefore this bias is not easily seen.
A related bias that also affects extragalactic distance determinations is the fact that there are larger numbers of objects at larger distances and therefore within a given range of estimated distances, more will be scattered by errors from larger to smaller distances than from smaller to larger ones.
Galactic absorption: Interstellar gas and
dust absorbs the
background light with dust scattering more efficiently the blue light, and
thus the background light appears artificially reddened. From simple
geometrical considerations it is easy to show that the flux
l of an
extragalactic source, transversing a Galactic layer of thickness
ds, at an
angle b from the equatorial plane, suffers losses
of an
extragalactic source, transversing a Galactic layer of thickness
ds, at an
angle b from the equatorial plane, suffers losses
 l
l /
l
/
l
 ds
cosec(b) and therefore:
ds
cosec(b) and therefore:

| (47) |
where the constant of proportionality

 is the absorption
coefficient at the spectral frequency
is the absorption
coefficient at the spectral frequency
 . Therefore, integrating we
have:
. Therefore, integrating we
have:

| (48) |
where the integration constant
l o
is the incident and
l
o
is the incident and
l is the
observed flux, while
is the
observed flux, while 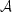 =
= 

 ds
is the optical thickness. Therefore to take into
account this effect (36) should change to:
ds
is the optical thickness. Therefore to take into
account this effect (36) should change to:

| (49) |
Values of 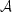 slightly
vary for different spectral frequency bands, but a
generally accepted value, in V, is ~ 0.2. We see from (49) and (39) that
slightly
vary for different spectral frequency bands, but a
generally accepted value, in V, is ~ 0.2. We see from (49) and (39) that

| (50) |
ie., the distance of an extragalactic source at a given absolute magnitude can be significantly overestimated at low galactic latitudes if this effect is not taken into account. Note however that the cosec(b) model is oversimplified since the distribution of gas and dust in the Galaxy is rather patchy.
Cosmological Evolution: As we look back in time we see a distribution of extragalactic objects (normal galaxies, AGN's, clusters) in different evolutionary stages. It may well be that their luminosity and/or mean number density is a function of cosmic time, a fact that will affect distance determinations based on local calibrations of the relevant scaling-relations.
Aperture effect: Since galaxies are extended objects with no sharp outer boundaries, their photometric measures will depend also on the size of the telescope aperture since at different distances different fraction of a galaxy will fit in the aperture. This is a distance-dependent effect, since diameters scale like 1 / r, and therefore it may affect the distance estimate.