2.3. Distance Indicators

In order to develop the distance ladder from local to distant cosmic objects, one starts from the local distance scale (for a detailed account see [143], [144]).

Galactic Distance Indicators: The primary method used to estimate the distances to nearby stars is that of Trigonometric Parallax. As the Earth orbits the Sun, we view the Universe from different points of the orbit throughout the year. This difference is maximum every 6 months when the Earth is on the opposite side of its orbit around the Sun. This kinematic method provides the basic unit of distance, the parsec, used by astronomers. It is defined as the distance at which a star would have a trigonometric parallax of 1" (parsec = parallax + second):

Note that this method is effective out to ~ 60 parsecs and that the nearest star to us (-Centauri) is at a distance of 0.75 parsecs.

Among the many distance indicators, used to determine distances within our Galaxy, a particularly interesting one is the Main sequence fitting method. This takes advantage of the fact that stars in globular clusters are at a common distance and that there is a unique correlation between spectral stellar type and absolute luminosity (the H-R diagram). Therefore by measuring the distance, via a kinematic method, to one relatively near globular cluster, one sets the zero-point of this method and then by observing the apparent magnitude - spectral type distribution of other globular clusters, one can determine their distance.

Extragalactic Distance Indicators: The next step is based on Cepheid Variable Stars. This method has been traditionally used within our Galaxy and in the nearby Large Magellanic Cloud (LMC), but with the Hubble Space Telescope it has been successfully used out to ~ 20 Mpc (cf. [61]). A strong and tight relationship exists between the intrinsic luminosity of these stars and their period of variation (pulsation) which results in a Period-Luminosity relation:

(51)

Once this relation has been calibrated, it provides the absolute luminosity of the distant Cepheid stars and via (39), the distance of their host galaxy. Although this relation has a scatter, in the I-band, of only ±0.1 mag, systematic effects may exist. For example, a serious concern is whether there is any environmental dependence of the relation. It has been suggested that a different metalicity of the host galaxy may significantly affect the zero-point of the relation and thus the determined distance. These effects can be taken into account and this method has proved to be fundamental in the recent determinations of H₀, because it provides the link between the primary galactic indicators and the local extragalactic ones, which then provide the calibration for other secondary indicators operating in much larger distances (cf. [61] and references therein).

In developing the distance scale, we now need effective indicators that can be used to very large distances. Other scaling relations have been found between a distance dependent (ex. brightness, diameter) and a distance independent (ex. rotational velocity, stellar velocity dispersion) quantity. It is evident that from such relations one can extract distance information. The main assumption in such a use of these scaling relations is that they are not environment-dependent (which has been shown to be a valid assumption). Such a relation for spiral galaxies is the Tully-Fisher relation [175], which relates the rotational velocity of a spiral to its total infrared luminosity: L_ir V_rot⁴ or its total blue luminosity: L_b V_rot with ~ 2.4 -2.8. It has a reasonable theoretical justification: Rotational velocities in spirals are related to mass according to

(52)

Assuming that all spirals have the same surface brightness S, then

(53)

If the mass to light ratio is constant then

(54)

For ellipticals a similar relation holds, the Faber-Jackson relation [60], which relates the absolute luminosity of the galaxy with the stellar velocity dispersion (L ^3-4) or a variant, the so-called D_n - relation (cf. [50]), which relates the diameter D_n of an elliptical (defined as that within which the mean surface brightness is 20.75 mag arc sec^-2 in B) to the stellar velocity dispersion : D_n ^x with x ~ 1.2 -1.3 . The typical accuracy of these distance estimations is ~ 20% and the usual assumption is that they do not evolve with redshift over the scales used, and that systematic effects can be corrected for. However, there are some indications for an evolution of the B-band Tully-Fisher relation in the interval studied 0.1 < z < 1 [195].

Another very important distance indicator, which can be used to large distances, is the Supernova SNIa brightness at maximum. It is thought that the maximum luminosity of such supernovae (explosion of white dwarfs in binary systems which become gravitationally unstable - reaching the Chandrasekhar limit - due to the accretion of matter from the secondary - see [92]) is a Universal constant and since the intrinsic luminosity of a SNIa is high, they can be seen out to cosmological distances. Furthermore, a correlation was found between the supernova luminosity and the brightness decay time, which provides a further parameter that reduces the scatter in luminosity to ±0.3 mags. Using this distance indicator one can construct the Hubble diagram to very large-distances and thus determine the deceleration of the Universe by mapping the region of the Hubble diagram that deviates from linearity. This has been recently achieved by two independent groups, the Supernova Cosmology Project - SCP [118] and the High-z Supernova Search Team - HZT [156], which have found that the derived Hubble diagram is that expected from a accelerating expansion, which can be provided by a non-zero cosmological constant (see Fig.5).

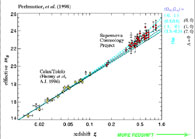
Figure 5. The SN Ia Hubble diagram vs Cosmological model predictions (from [119] with permission).

Direct Distance Indicators: Clusters of galaxies are filled with hot and transparent gas which can be fitted by a thermal Bremsstrahlung spectrum with t ~ 5 × 10⁷ -10⁸ k (covering a range of 2 ~ 8 KeV). The physics of the hot intercluster gas provides the means of measuring directly the distance of clusters, without need of intermediate steps. This method is based on the so called Sunyaev-Zeldovich effect which is the distortion of the original CMB spectrum, by the Compton scattering to higher energies of the CMB photons from the hot electrons of the plasma (for recent reviews see [131], [17]). This distortion decreases the brightness of the CMB spectrum at the longer wavelength range while it increases the photon energies in the shorter wavelength range. Lets assume a cluster of radius R at a distance D, subtending an angular separation on the sky. The change of the CMB brightness temperature is proportional to the line integral of electron number density through the cluster:

(55)

then from isothermality we get T/T T_e n_e R. Furthermore the luminosity of the Bremsstrahlung radiation together with the assumption of isothermality, gives:

(56)

From (56), the observed X-ray flux (F_x L_x / D²) and R = D we have:

(57)

and solving for D we get:

Therefore measuring F_x, , T_e we obtain an absolute determination of the cluster distance. The temperature, T_e, can be measured either from the shape of the X-ray continuum or from line emission (especially of iron). Note however, that we have assumed sphericity, isothermality and a smooth distribution of n_e. Most clusters are flattened (cf. [12]), and show significant substructure apparent in the optical and X-ray images. In such clusters the above procedure may provide highly uncertain and biased distance estimates (cf. [77]). A recent study of ~ 100 clusters has shown that once cooling flows are taken into account, isothermal profiles fit well ~ 90% of the clusters ([185], but see also [45]).