3.5. Cosmic microwave diminution (Sunyaev-Zel'dovich effect)

X-ray observations indicate that clusters of galaxies contain significant amounts of diffuse, hot gas. In this section and the next, the effect of this gas on sources of radio emission lying behind the cluster will be discussed. The free electrons in this intracluster plasma will have an optical depth for scattering low frequency photons given by

(3.4)

where _T = (8 / 3)[e² / (m_e c²)]² is the Thompson electron scattering cross section, n_e is the electron density, and l is the path length along any line of sight through the gas. For a typical X-ray cluster, n_e 10^-3 cm^-3 and l 1 Mpc, and thus _T 10^-(2-3). A fraction _T of the photons from any radio source behind a cluster will be scattered as the radiation passes through the cluster.

One 'source' of radio emission which lies 'behind' everything is the cosmic radiation which is a relic of the 'big bang' formation of the universe (Sunyaev and Zel'dovich, 1980a). This radiation has a spectrum that is nearly a blackbody, with a temperature of T_r 2.7 K. Because this radiation is nearly isotropic, simply scattering the radiation would not have an observable effect. However, because the electrons in the intracluster gas are hotter than the cosmic radiation photons, they heat the cosmic radiation photons and change the spectrum of the cosmic radiation observed in the direction of a cluster of galaxies. This effect was first suggested by Zel'dovich and Sunyaev (1969) (Sunyaev and Zel'dovich, 1972). Reviews of the theory and current observational status of this Sunyaev-Zel'dovich effect have been given recently by Sunyaev and Zel'dovich (1980a, 1981).

During an average scattering, a photon with frequency has its frequency changed by an amount / = 4kT_g / m_e c², where T_g is the electron temperature of the intracluster gas. In calculating the effect this has on the radiation spectrum, it is conventional to measure the intensity in terms of a 'brightness temperature' T_r; this is defined as the temperature of a blackbody having the same intensity. Then, the change in the brightness temperature of the cosmic radiation due to passage through the intracluster gas is given by

(3.5)

where I is the radiation intensity and x h / kT_r. This expression is actually derived in the diffusion limit and is valid only for sufficiently small x 10 (Sunyaev, 1981). The change in brightness temperature or intensity is negative for low frequencies x < 3.83 and positive for higher frequencies. This change occurs at a wavelength ₀ = 0.14 cm(2.7 K / T_r). It is somewhat paradoxical that heating the background radiation lowers its brightness temperature at low frequencies. This is because Compton scattering conserves the number of photons, and shifting lower frequency photons to higher energies lowers the intensity at low frequencies.

Nearly all of the measurements that have been made of this effect have been at relatively low frequencies; taking the limit x 0 in equation (3.5) gives

(3.6)

This reduction in the cosmic radiation in the direction of clusters of galaxies in the microwave region is often referred to as the 'microwave diminution'. Calculations of T_r and its variation with projected position for a large set of models for the intracluster gas have been given by Sarazin and Bahcall (1977), and specific predictions of the size of the effect for the Coma, Perseus, and Virgo/M87 clusters are given in Bahcall and Sarazin (1977). Models for the Coma cluster have been given by Gould and Rephaeli (1978) (but note that their basic model for the intracluster gas is not physically consistent) and Stimpel and Binney (1979) (these models included the effect of cluster ellipticity).

Unfortunately, it has proved to be very difficult to make reliable measurements of this very small microwave diminution effect. Pariiskii (1973) claimed to have detected a microwave diminution from the Coma cluster. Gull and Northover (1976) claimed to have detected both Coma and A2218, and found very small diminutions towards four other clusters. The claimed detections of Coma were at a level much too high to be consistent with models for the X-ray emission from this well-studied cluster (Bahcall and Sarazin, 1977; Gould and Rephaeli, 1978), and subsequent observations have not confirmed the microwave diminution in Coma. Rudnick (1978) gave upper limits for five clusters, including Coma; his limits were consistent with models for the X-ray emission, but inconsistent with the previously claimed detections of Coma. Lake and Partridge (1977) claimed three detections of very rich clusters, but later withdrew the claim, saying that the measurements were undermined by systematic problems with the telescope. In a later survey of 16 clusters (Lake and Partridge, 1980), they detected only A576 at a level of T_r = -1.3 ± 0.3 mK. (Note that 1 mK 10^-3 K). Birkinshaw et al. (1978, 1981b) surveyed 10 clusters, detecting microwave diminutions in A576 (T_r = -1.12 ± 0.17 mK), A2218 (T_r = -1.05 ± 0.21 mK), and possibly A665 and A2319. A2218 was not detected by Lake and Partridge (1980); in fact, their measurements have the opposite sign. Perrenod and Lada (1979) made measurement at higher frequencies ( = 9 mm >> _o) in order to reduce the effects of contamination by radio galaxies and beam smearing. They detected A2218 at the same level as Birkinshaw et al., and also had a marginal detection of A665 at T_r = -1.3 ± 0.6 mK (A665 is the richest cluster in the Abell catalog). Lasenby and Davies (1983) did not detect either A576 or A2218.

The apparent microwave diminutions from A576 and A2218 require very large masses of gas (comparable to the virial masses) at very high temperatures T_g 3 × 10⁸ K. X-ray observations of A576 are completely inconsistent with this much gas at these temperatures (Pravdo et al., 1979; White and Silk, 1980), and thus the measured microwave reductions must be due to some other effect. While earlier low spatial resolution studies of A2218 suggested that it was too weak an X-ray source to produce the claimed microwave diminution (Ulmer et al., 1981), a detailed high spatial resolution study of the X-ray emission from A2218 with the Einstein observatory (Boynton et al., 1982) indicates that the required amounts of gas are present in this cluster at the required temperatures T_g = 10 - 30 keV.

From equation (3.6), the microwave diminution effect is independent of distance as long as the cluster can be resolved. In fact, Birkinshaw et al. (1981a) have measured a diminution of T_r = -1.4 ± 0.3 mK from the distant (z = 0.541) cluster 0016+16. Optically, this is a rich cluster (Koo, 1981), although the field is somewhat confused by a foreground cluster at z = 0.30. There is a strong X-ray source towards 0016+16, which would imply a very high X-ray luminosity if it is associated with the more distant cluster (White et al., 1981b). In some ways, microwave diminution observations of distant clusters are more straightforward than observations of nearby clusters, because the reference positions are further outside the cluster core.

Recently, a new set of observations of the microwave diminution were published by Birkinshaw et al. (1984) (see also Birkinshaw and Gull, 1984). These observations used the Owens Valley Radio Observatory and are apparently less subject to systematic effects than earlier observations. They confirm the detections of 0016+16 (T_r = -1.40 ± 0.17 mK), A665 (T_r = -0.69 ± 0.10 mK), and A2218 (T_r = -0.70 ± 0.10 mK). Several of these detections have also been confirmed by Uson and Wilkinson (1985). Since there are now several confirming observations of the microwave diminution in these three clusters, it may be that the effect has finally been observed unambiguously. However, in view of the disagreements between different observers in the past, the withdrawal of previously claimed detections, and the inconsistency of some of the radio results with X-ray measurements of the amount of gas present, I do not feel completely confident that the current microwave diminution results are conclusive. It is clear that the major sources of errors in the measurements are not statistical but systematic. These include very low level systematic problems with the response of the radio telescopes used (Lake and Partridge, 1980).

One major source of problems is the possible presence of radio sources in the cluster. If these are concentrated at the cluster core, they will increase the radio brightness of the cluster and mask the microwave diminution. All of the observations are corrected for the presence of strong radio sources, and the observers generally avoid observing clusters, such as Perseus, which contain very strong radio sources. There is still the danger that a larger number of harder to detect, weaker radio sources will make a significant contribution to the cluster radio brightness. Birkinshaw (1978) surveyed six clusters, including A576 and A2218, for weak radio source emission, and concluded that it was unlikely to affect the microwave diminution measurements. Schallwich and Wielebinski (1978) detected a weak radio source in the direction of A2218, and corrected the microwave diminution measurement of Birkinshaw et al. (1978) for this cluster. Unfortunately, this correction would destroy the agreement of this measurement with the shorter wavelength measurement of Perrenod and Lada (1979), because the radio source and microwave diminution have different spectral variations. Tarter (1978) has suggested that if clusters contained a small amount of ionized gas at a cooler temperature than the X-ray emitting gas, the free-free radio emission from this gas could mask the microwave diminution. All of these radio source problems would generally mask the microwave diminution and might explain why some clusters that are predicted to have very strong diminutions, such as A2319, are in fact observed to have positive T_r.

What about A576, in which a strong microwave diminution was initially observed, although very little gas is observed in X-rays? The microwave diminution measurements are generally relative measurements in which one compares the cosmic microwave brightness in the direction of the cluster core with the brightness at one or more positions away from the cluster core. A negative T_r at the cluster core cannot be distinguished from a positive T_r in these reference positions, which are generally not far outside the cluster core. Thus the observation of a negative T_r in A576 may indicate that there is excess radio emission in the outer parts of the cluster. a href="Sarazin_refs.html#142" target="ads_dw">Cavallo and Mandolesi (1982) have suggested that this radio emission is produced by the stripping of gas from spiral galaxies in the outer parts of the cluster.

The microwave and X-ray observations of a cluster can be used to derive a distance to the cluster which is independent of the redshift (Cavaliere et al., 1977, 1979; Gunn, 1978; Silk and White, 1978). From equation (3.6), T_r depends on the electron density n_e, the gas temperature T_g, and the size of the emitting region. The X-ray flux f_x from the cluster depends on all of these, but also decreases with the inverse square of the distance to the cluster. Thus the distance can be determined by comparing the X-ray flux and the microwave diminution:

(3.7)

where D_A is the angular diameter distance (Weinberg, 1972), z is the redshift, _c is the angular radius of the cluster core (Section 2.7), T_g(0) is the gas temperature at the cluster center, and the coefficient of proportionality depends on the distribution of gas in the cluster and the X-ray detector response (Cavaliere et al., 1979). In fact, any assumptions about the gas distribution can be avoided by mapping the variation of both the X-ray surface brightness I_x and the microwave diminution as a function of the angle away from the cluster center . Silk and White (1978) find

(3.8)

where f is a known function of gas temperature, which for a hot solar abundance plasma contains only atomic constants. This determination of the distance to the cluster is independent of the distribution of the gas as long as it is spherically symmetric. Applying this method to nearby clusters and comparing the distances with the redshift could allow the determination of the Hubble constant h₀. Mapping high redshift clusters (z 1) could give the cosmological deceleration parameter q₀; together, these two parameters determine the structure, dynamics, and age of the universe (Weinberg, 1972), yet remain very poorly determined after a half century of observational cosmology research.

Unfortunately, the difficulty of obtaining reliable microwave diminution measurements has made it impossible to apply this method at the present time (Birkinshaw, 1979; Boynton et al., 1982). In general, cluster microwave diminutions have not been mapped with sufficient accuracy to allow the distance to be determined from equation (3.8). Even the optical data on clusters are not accurate enough to allow an accurate distance determination. In addition, the cause of false detections, such as A576, must be determined so that they can be weeded out of cluster samples. For example, if the detection of A576 were taken seriously, it would imply a distance to this cluster at least an order of magnitude more than its redshift distance (White and Silk, 1980).

Gould and Rephaeli (1978) suggested that it might be easier to detect the Sunyaev-Zel'dovich effect unambiguously at high frequencies ( < ₀) at which T_r is positive. Some observations have been attempted at = 1 - 3 mm (Meyer et al., 1983), but no cluster diminutions were detected, and this wavelength range straddles ₀. Observations at shorter wavelengths must be made from satellites.

Sunyaev and Zel'dovich (1981) point out that although their effect is often thought of as a small change in the cosmic microwave background, at < ₀ the effect may also be considered as an enormous source of submillimeter luminosity for the cluster. Because the surface brightness of the submillimeter emission is proportional to _T n_e l, where l r is the path length through the cluster and r is the radius of the gas, and the surface area is proportional to r², the luminosity is proportional to n_e r³ or the mass m_g of the gas in the cluster. The submillimeter luminosity at frequencies above the critical frequency ( < ₀) is given by

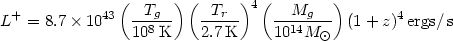
(3.9)

where the factor [T_r(1 + z)]⁴ gives the cosmic radiation density at the redshift of the cluster. Thus clusters could be among the strongest sources of submillimeter radiation in the universe. Other strong submillimeter sources, such as quasars, would have different spectra, be more compact, and probably be variable.

The variation in the cosmic microwave intensity and polarization toward a cluster can also be used to determine the velocity of the cluster relative to the average of all material in that region of the universe (Sunyaev and Zel'dovich, 1980b). This velocity, measured relative to the local comoving cosmological reference frame, is as near as one can come to an absolute measure of motion in a relativistically invariant universe. In a sense, the cosmic background radiation acts as an 'ether'. Just as the thermal motion of electrons in a cluster changes the wavelength of the cosmic background radiation during scattering, their bulk motion has a similar effect. As long as _T << 1, the variation in the brightness temperature due to cluster motion is independent of frequency and is given by

(3.10)

where v_r is the radial component of the velocity. The tangential component of velocity (the component in the plane of the sky) can be detected if the polarization of the microwave background in the direction of clusters can be measured to very high accuracy. At low frequencies (x << 1), the polarization (which is in the direction of motion) is

(3.11)

to lowest order in _T and _t v_t / c, where v_t is the tangential velocity.

The Sunyaev-Zel'dovich effect can also be used to determine the spectrum and angular distribution of the cosmic background radiation itself (Sunyaev and Zel'dovich, 1972; Fabbri et al., 1978; Rephaeli, 1980, 1981; Sunyaev, 1981; Zel'dovich and Sunyaev, 1981). In principle, the different causes of variations in T_r towards clusters (thermal motions of electrons, bulk motions, and variations in the cosmic background radiation itself) can be separated because they have different spectral variations (Sunyaev and Zel'dovich, 1981).

To summarize, the Sunyaev-Zel'dovich effect has a tremendous potential for providing information about the properties of hot gas in clusters and the nature of the universe as a whole. Unambiguous detections of this effect in clusters have proved elusive, but this situation may be improving.