3.6. Faraday rotation

A plasma containing a magnetic field is birefringent; the speed of propagation of an electromagnetic wave depends on its circular polarization (Spitzer, 1978). While natural sources of circularly polarized radiation are rare, synchrotron emission in an ordered magnetic field produces linearly polarized radiation, and many radio galaxies and quasars produce radio emission that is somewhat linearly polarized. The plane of polarization of linearly polarized radiation is rotated during passage through a birefringent medium. For a magnetized plasma, the angle of rotation is

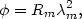
(3.12)

where it is conventional to give the wavelength _m of the radiationin meters. The rotation measure R_m is given by

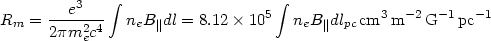
(3.13)

where l is the path length through the medium, B_|| is the component of the magnetic field parallel to the direction of propagation of the radiation, and n_e is the electron density. On the far right of equation (3.13), l is given in pc, n_e in cm^-3, and B_|| in gauss (G). The wavelength dependence of the rotation is the feature that allows the observational separation of the initial polarization angle and the amount of rotation.

The rotation measures to radio sources lying within or behind clusters can be used to constrain the magnitude of the intracluster magnetic field and its geometry (Dennison, 1980a; Jaffe, 1980; Lawler and Dennison, 1982). One problem with these determinations is that the rotation measure due to other plasma along the line of sight to the radio source must be removed. If this can be done, and the electron density and path length through the gas are determined from X-ray observations of the cluster, the average value of B_|| can be determined. Since this average of a single component of b must be less than the average magnitude of b, this gives a lower limit to the intracluster magnetic field. The Faraday rotation of the halo radio source in M87 in the Virgo cluster has been used to give a lower limit b 2µG (µG 10^-6 gauss) on the magnetic field in the gaseous halo around M87 (Andernach et al., 1979; Dennison, 1980a). This limit implies that very little of the X-ray emission from M87 can be nonthermal.

Jaffe (1980) noted that the rotation measures to radio sources within or behind clusters are generally small R_m 100m^-2, which for a cluster with n_e 3 × 10^-3 cm^-3 and a path length of 500 kpc gives B_|| 0.1µG. On the other hand, the halo radio emission observed in some clusters (Section 3.4) implies that the intracluster magnetic field strengths are B 1µG. Since it is unlikely that the fields are preferentially ordered perpendicular to our line-of-sight to each cluster, the difference in these two limits must be due to the cancellation of components of B_|| along the path through the cluster. Jaffe argues that this implies that the field is tangled. If this tangled field can be thought of as consisting of cells of ordered field of size l_B randomly oriented along the path length l through the cluster, then statistically <B_||> B(l_B / l)^1/2. Noting that only a portion of the rotation measure can be associated with the intracluster gas, Jaffe argued that the coherence length l_B of the intracluster magnetic field must be l_B 10 kpc. Since tangled fields in a static medium can straighten and decay rapidly, he suggests that the fields are tangled by the turbulent wakes produced behind galaxies as they move through the intracluster gas.

With a larger sample of radio sources and clusters, Lawler and Dennison (1982) claimed that the sources seen through rich clusters had slightly larger rotation measures, although the two distributions only differ at the 80% confidence level. Attributing the difference to intracluster Faraday rotation, they derived an average rotation measure of R_m 130m^-2 through the cluster center, which implies l_B 20 kpc; this is not inconsistent with the galactic wake model.

These limits on the strength and geometry of the intracluster B field are important to models for the X-ray emission for two reasons. First, the halo radio emission from a cluster depends on the product of the number of relativistic electrons and the magnetic field, and the relativistic electrons may heat the intracluster gas (Section 5.3.5). Second, the effectiveness of transport processes in the intracluster gas (such as thermal conduction) is determined by the geometry of the magnetic field because the gyroradius of electrons in even a very weakintracluster B field is very much less than the size of the cluster (Section 5.4.3).