


5.2.3. Resulting spectra
All of these emission processes give emissivities that increase in proportion with the ion and electron densities, and otherwise depend only on the temperature, so that
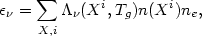
| (5.18) |
where  is the
emission per ion at unit electron density. If n(X) is the
total density of the element X, then in equilibrium the
ionization fractions f(Xi)
is the
emission per ion at unit electron density. If n(X) is the
total density of the element X, then in equilibrium the
ionization fractions f(Xi)
 n(Xi)/n(X) depend only on the
temperature, and equation (5.18) becomes
n(Xi)/n(X) depend only on the
temperature, and equation (5.18) becomes
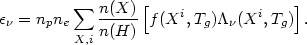
| (5.19) |
As previously noted (equation 4.3), it is useful to define the emission integral EI as
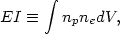
| (5.20) |
where V is the volume of the cluster. Then the shape of the spectrum depends only on the abundances of elements n(X)/n(h) and the distribution of temperatures d(EI) / dTg. The normalization of the spectrum (the overall level or luminosity) is set by EI.
Detailed calculations of the X-ray spectra predicted by different models of the intracluster gas have been given by Sarazin and Bahcall (1977) and Bahcall and Sarazin (1977, 1978). Figure (34) gives the X-ray spectrum for isothermal (Tg constant) models for the intracluster gas at a variety of different temperatures, showing the continuum and X-ray emission. The emission integral for these models was taken to be 6.3 × 10-7 cm-6 Mpc3.
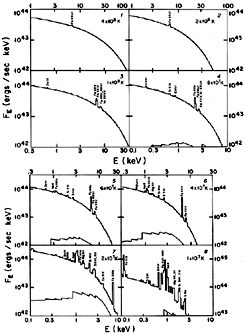
|
Figure 34. The predicted X-ray spectra of intracluster gas at various gas temperatures (shown at the upper right of each panel), from Sarazin and Bahcall (1977). The calculations assume the gas is isothermal, and the intensities are normalized to a sphere of gas with a proton number density of 0.001 cm-3 and a radius of 0.5 Mpc. E is the photon energy. The strongest line features are labeled; the lower curves, where present, show the bound-free emission. |
In these models most of the X-ray emission is thermal bremsstrahlung continuum, and the strongest lines (highest equivalent width) are in the 7 keV iron line complex. This line complex is a blend of K lines from many stages of ionization, although Fe+24 and Fe+25 predominate at typical cluster temperatures. As noted in Section 4.3.2, the 7 keV iron line is indeed the strongest line feature observed from clusters. Weaker lines at lower energies from lighter elements, such as oxygen, silicon, and sulfur, as well as from L shell transitions in less ionized iron were also predicted to be present in the spectra of clusters, particularly at lower temperatures. Such low energy lines have recently been detected (Section 4.3.3).
Because the line intensities depend on the abundances of heavy elements, while the continuum intensity is mainly due to hydrogen, the line-to-continuum ratio of a line is proportional to the abundance of the element responsible. This ratio is given by the equivalent width (equation 4.4). Figure 35 gives the equivalent width of the iron 7 keV line complex as a function of temperature in a gas with solar abundances. Comparison of these models to the observed strengths of the lines from clusters leads to the determination that the iron abundances are roughly one-half of solar (Section 4.3.2).
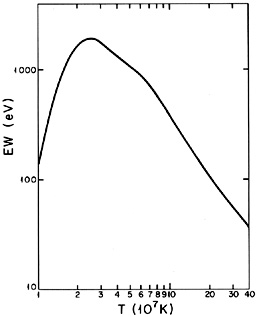
|
Figure 35. The equivalent width (in eV) of
the Fe K line at 7 keV as a function of gas temperature, from
Bahcall and Sarazin
(1978).
For gas temperatures
|
The spectral observations of clusters also indicate that in a number of cases the low energy X-ray lines are stronger than would be expected based on these hydrostatic models. This indicates that gas is cooling at the cluster center (Section 4.3.3).