5.3.5. Heating by relativistic electrons

Clusters of galaxies often contain radio sources having steep spectral indices (Section 3.1); the radio emission from these sources is believed to arise from synchrotron emission by relativistic electrons. These electrons (particularly the lower energy ones) can interact with the intracluster gas and may heat this gas (Sofia, 1973; Lea and Holman, 1978; Rephaeli, 1979; Scott et al., 1980). A relativistic electron passing through a plasma loses energy through Coulomb interactions with electrons within a Debye length of the particle, and through interactions with plasma waves on larger scales. The rate of loss by an electron with total energy m_e c² is

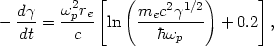
(5.30)

where _p is the plasma frequency (_p² 4 n_e e² / m_e), r_e e² / (m_e c²) is the classical electron radius, and n_e is the electron density in the plasma. The term in square brackets is 40 for most values of and n_e of interest, and does not vary significantly with either parameter. Numerically, the heating rate is 10^-18 n_e erg/s, ignoring the variation of the term in square brackets. The total heating rate is determined by multiplying this rate per electron by the total number of relativistic electrons in the intracluster gas. If the relativistic electrons have a power-law spectrum (equation 5.2), then the heating rate can be determined from the synchrotron radio emission rate given by equation (5.7). The heating rate is

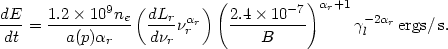
(5.31)

Here L_r is the radio luminosity at a frequency _r, _r is the radio spectral index, b is the intracluster magnetic field, a(p) is the function given by equations (5.4) and (5.8), and _l is the lower limit to the electron spectrum (equation 5.2). Cgs units are to be used for L_r and B. The first quantity in parentheses is independent of the frequency _r at which the radio source is observed. Equation (5.31) includes only electrons and should be increased to include the heating by ions, which do not produce observable radio emission. While the radio flux and spectrum can be measured directly, the magnetic field strength must be estimated from the radio observations (Section 3.6), and the lower limit to the electron spectrum is generally unknown.

This heating rate is significant only for radio sources with steep spectra which extend to very, very low frequencies. Lea and Holman (1978) used low frequency radio observations of clusters to determine the radio flux and spectral index, and found that the electron spectrum must extend down to _l 10(B / µG)^-1 if the heating rate is to be comparable to the X-ray luminosity of the cluster. These low energy electrons would produce radio emission at a frequency of about 400 Hz, which is about 10⁵ times too low to be observed. Extrapolating the radio spectrum from the lowest observed frequencies ( 26 MHz) down to these low frequencies increases the total number of relativistic electrons and the corresponding heating rate by about 10⁵. Thus the hypothesis that relativistic electrons provide significant heating to the intracluster gas according to equation (5.31) requires an enormous and untestable extrapolation of cluster radio properties.

Several authors have argued that the heating rate of equation (5.31) should be increased by collective plasma interactions between the relativistic electrons and the intracluster gas (Lea and Holman, 1978; Rephaeli, 1979; Scott et al., 1980). In these models, it is assumed that the relativistic electrons are streaming away from a powerful radio source at the center of the cluster. Rephaeli (1979) assumed that the streaming speed is limited by the Alfvén velocity, as has generally been argued (Jaffe, 1977; Section 3.4). Then he finds that the relativistic electrons excite Alfvén waves and lose energy at a rate of -d / dt v_A / L_e, where L_e is the scale length of the relativistic electron distribution. For B 1 µG, L_e 1 Mpc, and n_e 10^-3 cm^-3, this gives a heating rate about 10^-2 _l of that in equation (5.31), which is never very significant.

Alternatively, Scott et al. (1980) have assumed that the relativistic electrons stream at nearly the speed of light (Holman et al., 1979). As discussed in Section 3.4, this hypothesis is controversial. They discuss a number of plasma instabilities that greatly increase the heating rate under these circumstances. The increase could be as much as a factor of 10⁵, which would allow the electrons that produce the observed radio emission in clusters to heat the intracluster gas.

Models in which relativistic electrons heat the intracluster gas suffer from two general problems. First, the total energy requirements of 10^63-64 erg are extreme for a single radio source, although it is possible that many cluster sources contribute to the heating over the lifetime of the cluster. Second, the radio sources generally occupy only a small fraction of the cluster; cluster-wide radio haloes are rare (Section 3.4). It is difficult to see how several discrete radio sources would heat the intracluster gas without producing very strong, observable variations in the X-ray surface brightness, which are not seen.

Vestrand (1982) has suggested that heating of the intracluster gas by relativistic electrons is important only in clusters having radio haloes. He noted that Coma, which has a prominent halo, also has an unusually high gas temperature for its velocity dispersion (Section 4.5.1).