5.5. Distribution of the intracluster gas-hydrostatic models

In general, the elastic collision times for ions and electrons (equations 5.32, 5.33) in the intracluster gas are much shorter than the time scales for heating or cooling (Section 5.3) or any dynamical process, and the gas can be treated as a fluid. The time required for a sound wave in the intracluster gas to cross a cluster is given by

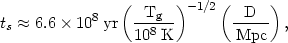
(5.54)

where T_g is the gas temperature and D is the cluster diameter. Since this time is short compared to the probable age of a cluster of 10¹⁰ yr, the gas will be hydrostatic and the pressure will be a smoothly varying function of position unless the cluster gravitational potential varies on a shorter time scale or the gas is heated or cooled more rapidly than this. The cooling time due to thermal bremsstrahlung (equation 5.23) is much longer than the sound crossing time, and the same is true for the time scales for heating by any of the processes that have been suggested (Section 5.3). Thus the gas distribution is usually assumed to be hydrostatic:

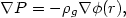
(5.55)

where p = _g kT_g / µm_p is the gas pressure, _g is the gas density, and (r) is the gravitational potential of the cluster. Now, the sound crossing time condition given above ensures that the pressure in the gas be uniform on small scales, but the same need not be completely true of the entropy. In the rest of this section, we will assume that the intracluster gas is locally homogeneous.

If, in addition, the cluster is assumed to be spherically symmetric, equation (5.55) reduces to

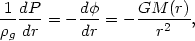
(5.56)

where r is the radius from the cluster center and m(r) is the total cluster mass within r. If the contribution of the intracluster gas to the gravitational potential is ignored, then the distribution of the intracluster gas is determined by the cluster potential (r) and the temperature distribution of the gas T_g(r). Further, then equation (5.56) is a linear equation for the logarithm of the gas density; the central density (or any other value) can be specified in order to determine the full run of densities. If self gravity is included, then the density scale, temperature variation, and cluster potential cannot be given independently.

In most models, the cluster potential is assumed to be that of a self-gravitating isothermal sphere (Section 2.7). For convenience, the analytic King approximation to the isothermal sphere is often assumed (equation 2.13), so that the cluster total density, mass, and potential are given by

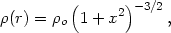
(5.57)

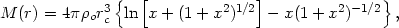
(5.58)

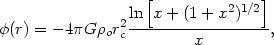
(5.59)

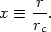
Here, ₀ is the central density and r_c is the core radius of the cluster (Section 2.7). The central density and core radius are related to the line-of-sight velocity dispersion _r (Section 2.6) of an isothermal cluster by

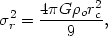
(5.60)

which follows from equation (2.9). Thus the central value of the cluster gravitational potential is

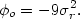
(5.61)

It is perhaps worth noting that although the analytic King model is a good fit to the inner portions of an isothermal sphere, the analytic King potential has a finite depth (given by equation 5.61), while the isothermal sphere potential is infinitely deep. The total mass associated with the analytic King distribution diverges as the radius increases, and it is usual to cut the distribution off in some way (equations 2.11 and 2.12). The effect of these cutoffs on the cluster potential and on the resulting hydrostatic gas models is discussed in Sarazin and Bahcall (1977) and Bahcall and Sarazin (1978).

In calculating the cluster potential, we have ignored the effect of individual galaxies. The potential wells associated with individual galaxies are considerably shallower than those associated with clusters. This is shown by the fact that the velocity dispersions of stars in galaxies (_* 300 km/s; Faber and Gallagher, 1979) are much smaller than the velocity dispersions of galaxies in clusters (_r 1000 km/s); the gravitational potentials increase with the square of the velocity dispersions. Thus an individual galaxy will not significantly perturb the distribution of intracluster gas (Gull and Northover, 1975).