5.5.2. Adiabatic and polytropic distributions

The intracluster gas will be isothermal if thermal conduction is sufficiently rapid (Section 5.4.2). On the other hand, if thermal conduction is slow, but the intracluster gas is well-mixed, then the entropy per atom in the gas will be constant (Section 5.4.6). In an adiabatic gas, the pressure and density are simply related,

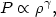
(5.75)

where is the usual ratio of specific heats and is = 5/3 for a monatomic ideal gas. While the value of 5/3 would be expected to apply if the intracluster gas were strictly adiabatic, equation (5.75) is often used to parametrize the thermal distribution of the intracluster gas, with taken to be a fitting parameter. For example, = 1 implies that the gas distribution is isothermal. Intracluster gas models with an arbitrary value of are often referred to as 'polytropic' models, and is called the polytropic index. Intracluster gas models with the polytropic index > 5/3 are convectively unstable (equation 5.52), and thus hydrostatic polytropic models must have 1 5/3.

Adiabatic and polytropic intracluster gas distributions were introduced by Lea (1975), Gull and Northover (1975), and Cavaliere and Fusco-Femiano (1976). Given equation (5.75), the hydrostatic equation (5.55) can be rewritten by noting that

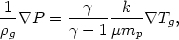
(5.76)

so that

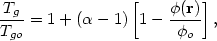
(5.77)

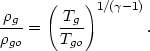
Here, ₀, T_go, and _go are the central values of the cluster gravitational potential, the intracluster gas temperature, and the density, respectively. In nonspherical clusters, 'central' means the lowest point in the cluster gravitational potential.

From equation (5.77), it is clear that the intracluster gas temperature will always decrease with increasing distance from the cluster center in adiabatic or polytropic models.

The integration constant is defined as

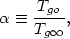
(5.78)

where T_g is the gas temperature at infinity. If > 0, the gas distribution extends to infinity, and the gas is not gravitationally bound to the cluster. If < 0, the gas extends only to a finite distance at which (r) / = < img src="../../New_Gifs/alpha.gif" alt="alpha"> / ( - 1), and the gas is gravitationally bound to the cluster. In the > 0 models, the intracluster gas connects with and is confined by intercluster gas, whose temperature is given by T_g . In general, the central gas temperature is given by

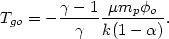
(5.79)

The enthalpy per particle in these models is a constant, both spatially and temporally, and is given by h = [ / ( - 1)]kT_go. Thus models with 0 cool very rapidly (Bahcall and Sarazin, 1978). Reasonable bound, intracluster gas models therefore usually assume 0.1.

If equation (5.59) is used for the cluster potential, then the gas density and temperature are analytic functions of radius in the cluster, but are sufficiently complex that the integrals for emission measures, masses, and so on are not analytic. Moreover, since the gas is not isothermal, the X-ray surface brightness and the emission measure are not simply related. Spectra, X-ray surface brightness profiles, masses, microwave diminutions, and a number of other quantities for these models are given in Sarazin and Bahcall (1977) and Bahcall and Sarazin (1978). Fits of these models to the surface brightness and spectra of a number of clusters are given in Bahcall and Sarazin (1977) and Mushotzky et al. (1978).