5.4.2. Thermal conduction

In a plasma with a gradient in the electron temperature, heat is conducted down the temperature gradient. If the scale length of the temperature gradient l_T T_e / | T_e| is much longer than the mean free path of electrons _e, then the heat flux is given by

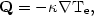
(5.36)

where the thermal conductivity for a hydrogen plasma is (Spitzer, 1956)

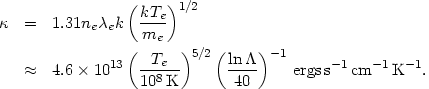
(5.37)

Because of the inverse dependence on the particle mass, thermal conduction is primarily due to electrons. This equation includes a correction for the self-consistent electric field set up by the diffusing electrons. If the very weak dependence of ln on density is ignored, then is independent of density but depends very strongly on temperature.

If the scale length of the thermal gradient l_T is comparable to or less than the mean free path of electrons, then equation (5.36) overestimates the heat flux, since it would imply that the electrons are diffusing at a speed greater than their average thermal speed. Under these circumstances the conduction is said to 'saturate', and the heat flux approaches a limiting value Q_sat. Cowie and McKee (1977) calculate this saturated heat flux by assuming that the electrons have a Maxwellian distribution, and an infinitely steep temperature gradient, and that the correction for a self-consistent electric field is the same as in the unsaturated case. They find

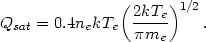
(5.38)

A general expression for the heat flux, which interpolates between the two limits of equations (5.36) and (5.38), is then

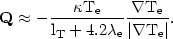
(5.39)

The mean free path of electrons in the intracluster gas (equation 5.34) is typically small compared to the cluster dimensions, and heat conduction within the intracluster gas itself is probably unsaturated. However, the mean free path is comparable to the size of a galaxy, and saturated heat conduction may be important in evaporation from or accretion to galaxies (Sections 5.7 and 5.9).

Within the intracluster medium, thermal conduction will act to transport heat from hot to cold regions and, in the absence of any competing effect, to make the temperature spatially constant (isothermal). Assuming equal ion and electron temperatures, the temperature in a Lagrangian element of the intracluster gas will vary as

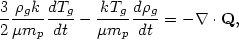
(5.40)

where _g is the gas density. It is useful to define a conduction time scale as t_cond -(d ln T_e / dt)^-1, which is on the order of |t_cond| (n_e l_T²k) / . As a specific example, consider a cluster in which the gas is hydrostatic, adiabatic (isentropic), and extends to very large distances but is not in contact with any intercluster gas; such models are discussed in some detail in Section 5.5.2 below. If the cluster potential is given by the analytic King form (equation 5.59 below), the gas is assumed to cool isobarically (at constant pressure), and the variation of ln is ignored, then the conduction time at a radius r is given by

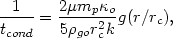
(5.41)

where ₀ and _go are the conductivity and gas density at the cluster center, and r_c is the cluster core radius. The function g(x) is

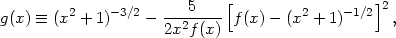
(5.42)

where f(x) (r) / ₀ is the ratio of the cluster potential to its central value and is given by equation (5.59) below. The function g(x) is plotted in Figure 36. Because conduction only transports heat, the average temperature of the gas is not changed; in the inner parts the gas is cooled and in the outer parts the gas is heated. However, because the X-ray emission is proportional to the square of the density, temperatures determined from X-ray spectra are mainly affected by the innermost gas and are lowered by conduction. As is clear from Figure 36, heat conduction is most effective in the cluster core, and |t_cond| increases very rapidly with radius. Since g(0) = 1, the central value to the conduction time scale t_cond(0) is given by the first term in equation (5.41), or

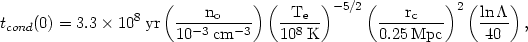
(5.43)

where n₀ is the central proton density, and solar abundances have been assumed. Thus heat conduction may be relatively effective in the core of a cluster. At radii r 2r_c, the conduction time is typically a factor of 100 longer, and conduction is only marginally effective in the outer parts of the cluster. The conduction time may be increased further by the presence of a magnetic field in the cluster.

Figure 36. The conduction time as a function of position in an adiabatic model for the intracluster gas. The conduction time is relative to its central value, and the radius is in units of the cluster core radius rc. The solid (dashed) curve indicates the portion of the cluster where the gas is cooled (heated) by conduction.