Annu. Rev. Astron. Astrophys. 1994. 32: 319-70 Copyright © 1994 by . All rights reserved

2.3. The Correlation Function

It is conventional in CMB work to expand the temperature fluctuations in spherical harmonics

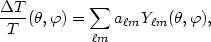
(3)

and work in terms of the multipole moments a_m. One can define the sky correlation function

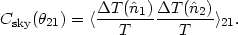
(4)

where the average is taken over the (observed) sky with the separation angle ₂₁ held fixed. Using the properties of Y_m the correlation function C_sky(₂₁) (hereafter we will drop the subscript "sky") is

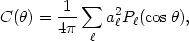
(5)

where we have introduced the rotationally symmetric quantity a² _m |a_m|². The a² are not to be confused with (2 + 1) C (see later) which is often used to define the power spectrum of fluctuations in a Gaussian theory. At this point we have made no assumption about the underlying theory of fluctuations or the model of structure formation - the a² are purely measured quantities on the sky. [Note that other authors' definitions of various quantities can differ from ours by 4, (2 + 1), or similar factors.] The COBE team (C. Bennett et al 1992, Kogut et al 1993, Fixsen et al 1994, Bennett et al 1994) quote results for the first two moments, i.e. a T₀ / (4) for = 1, 2,

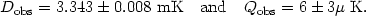
(6)

A common way of comparing theory and experiment is through the a_m. Of course an actual measurement of a temperature difference on the sky involves finite resolution and specific measurement strategies modifying Equation 5. These are usually included in the theoretically predicted correlation function through a window or filter function, W, described in Section 4.2.