Annu. Rev. Astron. Astrophys. 1994. 32: 319-70 Copyright © 1994 by Annual Reviews. All rights reserved

2.4. Fluctuations

Both inflation and defect models predict that the fluctuation spectrum should be stochastic in nature. Thus we live in one sample of an ensemble of "possible universes" which was drawn from a distribution specified by the underlying theory. Due to the weak coupling nature of most inflationary theories, the distribution of fluctuations is predicted to be Gaussian. (The assumption of Gaussian fluctuations is not to be confused with the further restrictive assumption of a Gaussian shape for the power spectrum.) In contrast, most defect models predict a non-Gaussian character for the fluctuations.

As discussed in Section 2.2, on large (e.g. COBE) scales fluctuations in almost all theories will look Gaussian. On smaller scales there is the possibility of detecting non-Gaussian phase correlations. There have been several tests for non-Gaussian fluctuations proposed, e.g. the total curvature or genus of isotemperature contours (Coles 1988b, Gott et al 1990, Brandenberger et al 1993, Smoot et at 1994), the distribution of peaks (Sazhin 1985, Zabotin & Nasel'skii 1985, Bond & Efstathiou 1987, Vittorio & Juszkiewicz 1987, Coles & Barrow 1987, Coles 1988a, Gutierrez de la Cruz et al 1993, Cayon et al 1993c, Kashlinsky 1993b), skewness and kurtosis of the observed temperature distribution (Scaramella & Vittorio 1991, 1993a; Luo & Schramm 1993a; Perivolaropoulos 1993b; Moessner et al 1993), or the 3-point function (Falk et al 1993, Luo & Schramm 1993b, Srednicki 1993, Graham et al 1993). Of these, the 3-point function currently seems the most promising, although more work is needed to see if it can detect departures from Gaussianness at the level predicted by the "defect" theories.

In general, the predictions of a theory are expressed in terms of predictions for the a_m. If the fluctuations are Gaussian, the predictions are fully specified by giving the 2-point function for the a_m [just as the matter spectrum P_mat(k) is predicted by giving (r)]. Using rotational symmetry, it is conventional to write

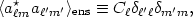
(7)

where the angle brackets here represent an average over the ensemble of possible universes. The prediction for CMB anisotropy measurements of a theory can thus be expressed as a series of Cs. Alternatively one can work in k-space and define a (3-dimensional) power spectrum of fluctuations per wavelength interval. We describe this, and its relation to the Cs, in Section 3.2. For large , the Cs are approximately the same as the 2-dimensional power spectrum of fluctuations (Bond & Efstathiou 1987).

2.4.1    ADIABATIC    Any initial density perturbation may be decomposed into a sum of an adiabatic and an isocurvature perturbation. Since inflation naturally predicts adiabatic density perturbations, we will consider these first.

Adiabatic modes are fluctuations in the energy density, or the number of particles, such that the specific entropy is constant for any species i (assumed nonrelativistic here):

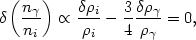
(8)

In terms of the perfect fluid stress-energy tensor of general relativity the assumption of an adiabatic perturbation is equivalent to assuming that the pressure fluctuation is proportional to the energy density perturbation. For a discussion of the classification and behavior of adiabatic perturbations in relativity see Kolb & Turner (1990), Efstathiou (1990), Mukhanov et al (1992), and Liddle & Lyth (1993).

It has been the standard assumption that inflation predicts a "flat" or Harrison-Zel'dovich (n = 1) spectrum of adiabatic density fluctuations. Recently, with the advent of the COBE measurement, it has been emphasized that inflation generically predicts departures from the simple n = 1 form. In "new" inflation, the departure is logarithmic, e.g. P_mat(k) k log³(k / k₀), with k₀ ~ e⁶⁰ Mpc^-1 - this can lead to an effectively tilted spectrum between say, COBE scales and more traditional normalization scales (typically n 0.95) even though the spectrum is "flat" on large scales. In "power-law", "chaotic", "natural", or "extended" inflation, one can have power law spectra with n < 1. Exotic models of inflation even allow n > 1 (Mollerach et al 1993).

On scales larger than the horizon size at last scattering (i.e. ~ 2°), the generation of temperature fluctuations from density inhomogeneities is straightforward to analyze. In addition to fluctuations in the temperature on the surface of last scattering (due to fluctuations in the radiation energy density), the matter perturbations give rise to potentials on the scattering surface and possibly time-dependent perturbations in the metric. Any time dependence (such as gravity waves, to be discussed later) leads to energy nonconservation along the photon line of sight. The potentials give rise to a "red"-shifting of photons as they leave the last scattering surface. To first order in the perturbing quantity, the total energy change of a photon (above and beyond the cosmological redshifting) from the time it leaves the last scattering surface (emission) is the integral along the unperturbed path of the (conformal) time derivative of the metric perturbation (h_µ), plus the change in the potential between last scattering and observation (see Appendix B):

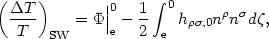
(9)

where n is the direction vector of the photon and is a parameter along the line of sight. If h_µ is due solely to density perturbations, the integrand is basically 4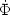, where the overdot represents a (conformal) time derivative. Either or both of these terms are known as the Sachs-Wolfe effect. The simplest part is the potential difference between the last scatterers and the observer. [The other (integral) term is usually associated with a background of gravitational waves, nonlinear effects, or ₀ < 1 universes - see later.] To this energy shift must be added the temperature fluctuation on the last scattering surface itself. For fluctuations in the radiation field, we have

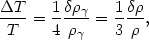
(10)

where the second equality follows from the adiabatic condition. Because an overdensity gives a larger gravitational potential / = 2 + [(k / H)²] that a photon must climb out of, for adiabatic fluctuations, the two terms partially cancel. One finds that T / T = - 1/3 . The minus sign means that CMB hot spots are matter under-densities.

2.4.2    ISOCURVATURE    Isocurvature modes are fluctuations in the number density of particles which do not affect the total energy density. They perturb the specific entropy or the equation of state,

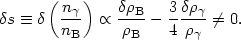
(11)

While such perturbations are outside the horizon, causality precludes them from becoming an energy density perturbation. Inside the horizon, however, pressure gradients can convert an isocurvature perturbation into an energy density fluctuation.

The possibility of scalar isocurvature fluctuations is not well motivated by usual inflation models, although if more than one field contributes significantly to the energy density during inflation one can get isocurvature fluctuations (the energy density fluctuation is no longer proportional to the pressure fluctuation). For isocurvature fluctuations, a positive fluctuation in the matter density (and therefore the gravitational potential) is compensated by a negative fluctuation in the photon temperature. The Sachs-Wolfe effect and the initial temperature fluctuation therefore add (rather than cancel as in the adiabatic case), giving rise to six times more large-scale T / T for a given "matter" perturbation. For this reason, isocurvature cold dark matter models that are normalized to give the observed peculiar velocities predict too large a temperature anisotropy in the CMB.

Specifically, CDM isocurvature models with roughly scale-invariant (i.e. m = - 3) power spectra (e.g. in the axion model of Axenides et al 1993) are probably ruled out (Efstathiou & Bond 1986). The situation is similar for HDM (Sugiyama et al 1989). Scale-invariant baryon-dominated models are also in serious conflict with the microwave background anisotropies (Efstathiou 1988), and cannot be saved even by invoking a cosmological constant (Gouda & Sugiyama 1992). However, models with larger in are not as yet ruled out (see also Efstathiou & Bond 1987). Isocurvature fluctuations are these days only discussed in terms of the Baryonic Dark Matter model. This is an observationally-motivated model, with low ₀ in baryons only. The large fluctuations generated at small scales have to be erased by the reheating due to some early collapsed objects. The effects of such a reionization will be discussed later. Constraints from anisotropies on scales 1° (Peebles 1987b, Sugiyama & Gouda 1992), from the Vishniac effect at small scales (Efstathiou 1988, Hu et al 1994), from spectral distortions (Daly 1991, Barrow & Coles 1991), and from the clustering properties of galaxies (Cen et al 1993) imply that only models with -1 m 0 are viable. High values of ₀ and high values of h which enhance the "bump" also tend to be ruled out. It has recently been shown (Sugiyama & Silk 1994) that the BDM picture generally leads to an effective slope n_eff 2 for the radiation power spectrum on large scales. Fluctuations on smaller angular scales depend on a number of tunable parameters, making BDM complicated to constrain in practice (Hu & Sugiyama 1994b, c).

2.4.3    GRAVITATIONAL WAVES    Until now, we have focused on the anisotropies in the cosmic microwave background arising from density perturbations in the early universe. In many models, there is also the possibility that a stochastic background of long-wavelength gravitational waves (GW) can be produced (Starobinskii 1979); for a discussion of inflationary models in this context see Rubakov et al (1982), Adams et al (1992), and Liddle & Lyth (1993). If such a background were to exist, it would leave an imprint on the CMB at large scales through the Sachs-Wolfe effect (Fabbri & Pollock 1983, Abbott & Wise 1984c, Starobinskii 1985, Abbott & Schaefer 1986, Fabbri et al 1987, Linder 1988b, White 1992). With the advent of the COBE measurement of the power at large scales, many authors addressed the question of the interpretation in terms of scalar and tensor contributions (Krauss & White 1992, Liddle & Lyth 1992, Adams et al 1992, Salopek 1992, Lucchin et al 1992, Dolgov & Silk 1993).

If there is a sizable contribution from GW in the COBE-detected anisotropies, this would lower the predicted value of (T/T)_rms on smaller scales. This should be kept in mind when comparing degree-scale experiments or large-scale structure studies to power spectra normalized to COBE on large scales.

Unlike the anisotropies generated by scalar fluctuations (Section 3), those generated by (isocurvature) tensor perturbations, or GW, damp at scales comparable to the horizon (see e.g. Starobinskii 1985, Turner et al 1993, Atrio-Barandela & Silk 1994), which means ~ sqrt[1 + z_rec] 30 (see Appendix A). This can be understood as due to the redshifting of GW that entered the horizon before recombination. The maximal contribution to the anisotropy on some scale comes from gravitational waves with wavelengths comparable to that scale. GW begin to redshift after they enter the horizon; thus scales that are smaller than the horizon at last scattering are dominated by GW that have redshifted before the photon begins to travel to us. The different behavior at small scales leads one to hope that the two contributions could be disentangled. A detailed numerical analysis of the anisotropy generated by GW on both large and small scales has been carried out by Crittenden et al (1993a).

In general, GW provide a small contribution to T / T on top of the scalar anisotropy. One requires a comparison of both large- and small-scale temperature anisotropies to isolate them. On large scales, one must deal with cosmic variance; on small scales one has sample variance and uncertainties due to cosmological parameters and history, which are far from orthogonal. The situation with regard to disentangling a gravitational wave signal is somewhat confused. White et al (1993) claim that cosmic variance and cosmological model uncertainty makes such a detection extremely difficult, while Crittenden et al (1993a) predict that a definitive detection is possible. [The analysis assumed a specific form for the relation between the spectral index and the ratio of scalar and tensor contributions to the quadrupole: T / S = 7(1 - n) (R. Davis et al 1992). This form requires correction for most theories (Liddle & Lyth 1992, Kolb & Vadas 1993) and also biases the fit towards "detection" of a tensor component. In addition, recent work (Bond et al 1994) suggests that including uncertainties in cosmological history may alter Crittenden et al's conclusions regarding gravity waves.] This question is of some importance, since any possible GW signal will affect the power spectrum normalization inferred from COBE. Since the GW production predicted in most theories is very small [for n 0.9 as required by COBE and Tenerife (Hancock et al 1994) T / S 1], perhaps their only observable effect for some time will be in generating large angular scale CMB anisotropies (Sahni 1990, Krauss & White 1992, Souradeep & Sahni 1992, Liddle 1994, Turner et al 1993). The possibility that GW lead to an observable polarization in the CMB (Polnarev 1985) has been shown to be very small (Crittenden et al 1993b; however, see Frewin et al 1994).

In theories of inflation, the normalization of the spectrum of scalar fluctuations depends on both the inflation potential and its derivative at the epoch of fluctuation generation. In contrast, the tensor spectrum depends only on the value of the inflation potential at the same epoch. This fact coupled with the COBE measurement can be used to limit the scale of inflation (Rubakov et al 1982, Lyth 1985, Krauss & White 1992, Liddle 1994). In principle, one can also derive information about the inflation potential from both the tensor and scalar components of the CMB anisotropy (Liddle & Lyth 1992, R. Davis et al 1992, Salopek 1992). Recently, several authors have considered the possibility of reconstructing the "inflation" potential from CMB observations (Hodges & Blumenthal 1990; Copeland et al 1993a, b, 1994; Lidsey & Tavakol 1993; Turner 1993; see also Carr & Lidsey 1993) or of using relations between observable parameters as "tests" of inflation (R. Davis et al 1992, Bond et al 1994, but see Liddle & Lyth 1992, Kolb & Vadas 1993).