Annu. Rev. Astron. Astrophys. 1994. 32: 319-70 Copyright © 1994 by Annual Reviews. All rights reserved

4.3. Fitting Data

In comparing the theory of CMB fluctuations to the new measurements of the anisotropy on various scales, two primary techniques are used: the Bayesian likelihood function analysis and the frequentist likelihood ratio method (which is often calibrated using Monte-Carlo simulations). Both of these techniques have been discussed and compared in the review of Readhead & Lawrence (1992), and we will not discuss them in detail here.

It is perhaps important to emphasize, however, that the methods will lead to the same conclusions when the data set is "well-behaved," but can differ when the data are "unlikely" or atypical. Both methods have ways of testing for possible breakdowns in statistical assumptions (which are not always used). For example, conclusions of the Bayesian approach should be robust under changes of prior distribution, and conclusions of the frequentist approach should take into account the type-II error (the probability of accepting the hypothesis when the null hypothesis is true).

The computation of the likelihood function simplifies considerably if fluctuations are assumed to be Gaussian. This is because all the nonvanishing moments of the distribution can be related to the variance. For Gaussian-distributed fluctuations, the likelihood function is

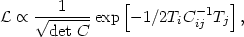
(31)

where T_i are the measured temperatures and C_ij is the auto-correlation matrix which includes a theoretical and experimental piece. In the limit that the experimental errors _i are uncorrelated we have

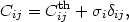
(32)

where C_ij^th is computed using Equation (30) or its generalization (see e.g. Bond et al 1991b; Dodelson & Jubas 1993; Dunn et al 1994b; Srednicki et al 1993; Bond 1993; Vittorio et al 1989, 1991; Vittorio & Muciaccia 1991; Górski et al 1993). Notice that the term in the exponent is just the ².

In the Bayesian approach, this function has to be multiplied by the "prior" to obtain the (relative) probability distribution for the parameters being fitted, while in the frequentist approach, the final distribution comes from ratios of likelihood functions or from Monte-Carlo simulation [see e.g. Berger (1985) for a discussion of these two philosophies].

It is also possible to fit more than one component to the data, in order to obtain the best constraints on the cosmic anisotropies. One example is in fitting an extra white noise component to the data (e.g. Bond 1993). Another example is the simultaneous fitting of a foreground signal of some given form (e.g. Dodelson & Stebbins 1993) to multichannel data. It is relatively straightforward to implement this idea (for either statistical approach), although there is some subjectivity in the choice of the number of parameters, which of them should be fixed (the frequency dependence of the foreground signal perhaps), and which to fit or integrate over. The fitting process becomes more computationally time consuming as more parameters are included.