Annu. Rev. Astron. Astrophys. 1994. 32: 319-70 Copyright © 1994 by . All rights reserved

5. BEYOND LINEAR THEORY

5.1. Reionization

A knowledge of the variation of optical depth (or equivalently the ionized fraction x_e) and of the peculiar velocities associated with different scales are enough to calculate T / T(). Reionization will erase the fluctuations generated at z ~ 1000, by making the Universe optically thick at much lower redshifts, but in the process extra fluctuations will be generated due to the motions of the new last scatterers. Because reionization cad be used to erase the primordial fluctuations in a model that would otherwise conflict with experimental upper limits, it is important to be able to calculate the secondary fluctuations so that the minimal level of anisotropy can be estimated.

The dominant contribution to anisotropies generated during reionization are Doppler shifts of the scatterers (Equation 23). The first (analytic) considerations of the velocity-induced perturbations in a reionized model were by Sunyaev (1977, 1978), Davis (1980), and Silk (1982). However Kaiser (1984) pointed out that an important term contributing to the fluctuations had been neglected in the previous work. The correct expression for T / T could not be written quite as straightforwardly as in Equation (2). The evolution of the radiation fluctuations needs to be followed more accurately, and requires a numerical solution of the collisional Boltzmann equation for the photons (see Section 3.2).

Ostriker & Vishniac (1986) extended the discussion to second-order fluctuations (see Section 5.2); detailed calculations are presented by Vishniac (1987), Efstathiou & Bond (1987; also Efstathiou 1988) made further calculations of the effects of reionization, including details of the pattern of polarization and approximations valid for small angular scales. The important effects of reionization on anisotropies are at arc-minute scales, in particular, where primary anisotropies are expected to be erased, and approximate calculations can be used which are valid only for small angles and correspondingly for small wavelength perturbations. More recent calculations have been carried out for reionization in BDM models (e.g. Hu et al 1994), generic open universe models (Persi & Spergel 1993), CDM models (Hu et al 1994, Dodelson & Jubas 1994, Sugiyama et al 1993, Chiba et al 1993, Hu & Sugiyama 1994b, c), and for the case of decaying dark matter (Scott et al 1991).

An important epoch is the redshift at which the optical depth for photons becomes unity. Since Thomson scattering is independent of frequency, the evaluation of z_* (or equivalently _*) is relatively simple:

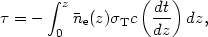
(33)

which, for an ₀ = 1 universe with a constant ionized fraction, becomes

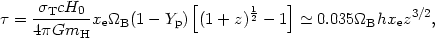
(34)

where Y_p is the primordial fraction of the baryonic mass in helium, which is assumed to be all neutral. Hence, for a particular model of the ionization history, the redshift for which = 1 can be calculated. For example, for constant ionization fraction z_* 69(h/0.5)^-2/3 (_B / 0.1)^-2/3 x_e^-2/3. For an open universe z_{* 0}^1/3 very approximately, so that the last scattering surface can be at significantly lower redshift. If the universe is ionized as early as z 100, then the exact z of reionization is unimportant, since then >> 1.

Reionization need not be complete, i.e. the optical depth may not become very large back to the new scattering surface. Obviously if 0.1 say, then reionization has negligible effect. This would be the case for a standard CDM model fully ionized even up to z ~ 20. However if 0.1 1, then a good approximation to the effects of erasure of the primary anisotropies (i.e. those generated at the standard recombination scattering surface) is that T / T is reduced by the fraction of photons scattered at z ~ 1000 rather than at the new scattering surface. If (1 - e^-_i) is the fraction of photons scattered since the Universe was reionized at z_i (i.e. this is the integral of the visibility function), then we simply have (T / T)_obs (T / T)_prim(e^-_i). There will also be secondary anisotropies generated on the new last scattering surface, although these will generally be smaller (see below). However, second-order fluctuations at much smaller angular scales also need to be considered.

Early reionization is likely to have been inevitable for COBE-normalized CDM [Tegmark et al (1994), Sasaki et al (1993), and Fukugita & Kawasaki (1994), following the early studies by Couchman (1985) and Couchman & Rees (1986)]. On scales of order the horizon at z_* there will still be Sachs-Wolfe fluctuations and the polarization would be expected to be higher.