Annu. Rev. Astron. Astrophys. 1994. 32: 319-70 Copyright © 1994 by . All rights reserved

5.2. Second-Order Anisotropies

The idea that reionization would erase the primary anisotropies, while generating smaller secondary Doppler anisotropies (since the new scattering surface was so thick), was overturned by the realization that the Vishniac effect played an important role at small angular scales. The first-order Doppler effects mainly cancel when the redshifts and blueshifts are integrated through the thick last scattering surface. 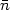However there is a second-order term in the Boltzmann equation (23) coming from the v cross term in _{T e} (1 + )v. In solutions to the Boltzmann equation at small scales, this term is a convolution over velocity and density perturbations, which does not suffer from the cancellation effect. This leads to sonic models giving larger secondary anisotropies than the primary anisotropies which the reionization was invoked to erase.

We can obtain a scaling relation for the Doppler fluctuations from the new last scattering surface as follows. Notice that the last scattering shell is at n_* with width ~ _*. The number of independent regions of scale lying across the thickness of the shell is N ~ _* / . The optical depth through each region of comoving scale is ~ 1/N ~ / _*. The fluctuations on scale ( ) are about N^1/2 times the fluctuation due to a single lump. The fluctuation for each lump is second-order because of the approximate cancellation of redshifts and blueshifts through a lump, leading to an effect ~ ²v (see Kaiser 1984). From the continuity equation, the peculiar velocity is v ~ _k(_*) / _* and overdensities evolve as ². Therefore an order-of magnitude estimate for the temperature fluctuations (i.e. k² , see also Kaiser 1984, Vishniac 1987) is

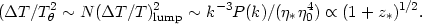
(35)

Hence earlier reionization generally leads to larger large-scale (first-order Doppler) fluctuations from the last scattering surface. Similarly for the second-order (e.g. Vishniac) fluctuations, the effect for each lump is ~ v, giving (T / T)² ~ k²P²(k)(1 + z_*)^-5/2. Again, this argument is crude, but shows that second-order small-scale fluctuations from the secondary last scattering surface would be expected to be smaller for earlier reionization. There are several experimental limits at scales ~ 1', which provide good constraints on these secondary fluctuations rather than the primary ones (e.g. Uson & Wilkinson 1984a, b, c; Readhead et al 1989; Fomalont et al 1993; Subrahmanyan et al 1993). The strong k dependence of the Vishniac effect means that the fluctuations will be very spiky, so that a double- or triple-beam experiment will be dominated by the zero-lag autocorrelation. Note, however, that nonlinear effects may also be important, e.g. if the universe is very clumpy, as may happen in BDM or other models with a large amount of small-scale power (Hu et al 1994), or if most of the baryons are trapped in galaxies at an early epoch (R. Juszkiewicz & P.J.E. Peebles, private communication).

In general, there are many second-order terms to consider once a fully second-order Boltzmann equation is derived (Hu et al 1994, Dodelson & Jubas 1994). For most of these terms, there will be a cancellation of redshifts and blueshifts (Kaiser 1984) through the last scattering surface, so that the major contribution to the fluctuations comes from modes with k-vector almost perpendicular to the lines of sight. The only significant term that remains is the Vishniac term, which is a convolution of v and , coupling large-scale velocity perturbations with small-scale density perturbations. In a model with significant reionization the primordial anisotropies are erased, a new Doppler peak is generated at smaller and of lower amplitude, and a Vishniac bump is generated at arc-minute scales. For CDM-type models, the Vishniac effect is negligible, but for models with a large amount of small-scale power and/or open models (e.g. BDM models, which also require reionization), the constraints can be restrictive. Generally the ionization history, x_e(z) can be varied in such models, since there is no clear picture for the process of early reheating. The Vishniac anisotropies tend to become smaller for an earlier last scattering surface, while the first-order amplitude becomes bigger; so there are limits to how much the constraints can be avoided by invoking a different ionization history (see Hu & Sugiyama 1994b, c).

Another kind of second-order anisotropy is that coming from nonlinear effects in the growth of perturbations, which causes the potential to change with time even in an ₀ = 1 universe. This change in potential in the light-crossing time across a fluctuation (Zel'dovich 1965, Rees & Sciama 1968, Dyer 1976) is known as the Rees-Sciama of integrated Sachs-Wolfe effect. It is small in almost all models (e.g. Argüeso & Martínez-González 1989; Martínez-González et al 1990, 1992, 1993, 1994; Anninos et al 1991), although large voids (Nottale 1984, Scaramella et al 1989, Thompson & Vishniac 1987, van Kampen & Martínez-González 1991, Arnau et al 1993), or structures such as the Great Attractor (Bertschinger et al 1990, Martínez-González & Sanz 1990, Hnatyk et al 1992, Goicoechea & Martin-Mirones 1992, Saez et al 1993) or the Great Wall (Atrio-Barandela & Kashlinsky 1992, Chodorowski 1992) etc might give observable signatures.