| Annu. Rev. Astron. Astrophys. 1994. 32:
319-70 Copyright © 1994 by . All rights reserved |
If the underlying fluctuation spectrum is assumed to be stochastic in nature, then one is faced with the problem of trying to compare a theory which defines probability distributions as functions of the underlying parameters with just one sample drawn from these (our Universe). Only observations over an ensemble of universes would allow one to determine the parameters of the underlying theory unambiguously, even in principle. Since we can observe only our universe, there is an irremovable uncertainty in our ability to relate certain CMB measurements, no matter how precise, to parameters of the theory. The uncertainty introduced in determinations of theoretical parameters has been called "cosmic variance" or "theoretical uncertainty" (e.g. Abbott & Wise 1984a, b; Scaramella & Vittorio 1990, 1991, 1993b; Cayón et al 1991; White et al 1993).
In terms of the multipole moments the cosmic variance may be thought of as an uncertainty in relating
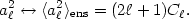
| (36) |
In a theory with Gaussian fluctuations, the
a
m are
independent Gaussian random variables and the
a2
are thus
22+1 distributed
(Abbott & Wise 1984a,
b;
Abbott & Schaefer 1986;
Vittorio et al 1988).
The uncertainty in relating a2 and
<a2>ens is given by the width
of the distribution, which scales as
( + 1/2)-1/2. As
one goes to smaller scales and probes larger
, one thus becomes less
sensitive to
cosmic variance. On large scales, however, cosmic variance forms the
limiting uncertainty in fixing (e.g.) the normalization of the power
spectrum. For the quadrupole (with only 5 degrees of freedom), the
actual amplitude in our Universe is likely to differ substantially
from its expectation value
(Gould 1993,
Stark 1993).
While it is true that on smaller scales, which probe higher
, the
cosmic variance becomes negligible, this applies only to a full sky
measurement. The variance from sampling only a fraction of the sky is
larger than the cosmic variance one gets when sampling the whole sky.
Since current small-scale experiments cover only small patches of the
sky, this can be an important effect. In general for an experiment
that samples a solid angle
, the cosmic
variance is enhanced by a factor of
4
/
(Scott et al 1994,
see also Bunn et al 1994a).
We should emphasize that this "sample variance" is completely independent
of the experimental precision, and simply reflects the fact that the
experiment has not covered enough of the sky to provide a good
estimate of the rms value of
T / T.
The spectrum of fluctuations
depends not only on the primordial spectrum but on the evolution of
perturbations as waves enter the horizon. This evolution introduces
dependencies on
0,
H0, and the dark matter. In addition, a
knowledge of the ionization history of the universe is important since
reionization would lead to both a reprocessing of primary fluctuations
and generation of (small-scale) secondary fluctuations. (See
Section 5.1.) A non-negligible ionized
fraction during much of the history of
the universe would also contribute a radiation drag which would affect
the growth of baryon perturbations and alter the observed CMB
anisotropy. In general, the uncertainties in the cosmological
parameters and history produce very correlated shifts in the radiation
power spectrum
(Bond et al 1994,
Hu & Sugiyama
1994b,
c).
In addition, there are possible sources of "foreground" contamination such as synchrotron and free-free emission (at low frequency) and dust (at high frequency), These non-cosmological sources have been discussed in detail in the review of Readhead & Lawrence (1992) and we will not mention them further except to say that to discriminate between these sources it is necessary to have good frequency coverage and a wide range of angular resolutions. Note that, in particular, the galactic signal also makes it difficult to measure the quadrupole anisotropy (de Bernardis et al 1991, Bennett et al 1994).