2.1. Alternative Approaches to Peculiar Velocity-Density Comparison
Before presenting our method in detail, we briefly review the principal alternatives. Two approaches are fairly paradigmatic and serve to illustrate the main issues and motivate our approach. These are the POTENT method of A. Dekel and coworkers (e.g., Dekel 1994; Dekel et al. 1997b) mentioned in Section 1, and the ITF method of Nusser & Davis (1995; DNW).
The POTENT algorithm is designed to reconstruct, from sparse and noisy radial peculiar velocity estimates, a smooth, three-dimensional, peculiar velocity field and the associated mass density field. The method is based on the property that the smoothed velocity field of gravitating systems is the gradient of a potential. The divergence of equation (3) is
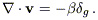
| (4) |
Thus, 
is the slope of the correlation between
. v,
obtained from POTENT,
and 
g,
obtained from redshift survey data. This is the basis of the POTIRAS
approach (4) to determining
I,
discussed above (Section 1).
POTENT has several advantages as a reconstruction method. It yields model-independent, three-dimensional velocity and density fields well suited for comparison with theory and for visualization. It works in the space of TF-inferred distances, i.e., it is a Method I approach to velocity analysis (cf. SW, Section 6.4.1). Unlike Method II approaches (see below), it does not assume that there is a unique distance corresponding to a given redshift. In regions where galaxies at different distances are superposed in redshift space, POTENT is capable of recovering the true velocity field. The POTIRAS comparison between the mass and galaxy density fields is entirely local (eq. [4]), whereas predicted peculiar velocities are highly nonlocal (eq. [3]). Locality ensures that biases due to unsampled regions are minimized.
The liabilities of POTENT are closely
related to its strengths. In order to construct a model-independent
velocity field, it must have redshift-independent distances as input. Such
distances require properly calibrated TF relations. In particular, the TF
distances for samples that probe different regions of the sky must be
brought to a uniform system, which is a difficult procedure (cf.
Willick et al.
1995,
1996,
1997).
Errors made in
calibrating and homogenizing the TF relations will propagate into the
POTENT velocity field. Because POTENT works in inferred distance space, it
is subject to inhomogeneous Malmquist bias
(Dekel et al. 1990).
Minimizing this bias requires significant smoothing of
the input data. POTENT currently employs a Gaussian smoothing scale
of 1000-1200 km s-1
(Dekel 1994;
Dekel et al. 1997b),
making it relatively insensitive to dynamical effects on
small scales. As a result, the current POTENT applications are not
particularly effective at extracting detailed information from the velocity
field in the local (cz
3000
km s-1) universe.
DNW take a
different approach. They work with the "inverse"
form of the TF relation
(Dekel 1994,
Section 4.4;
SW,
Section 6.4.4) and thus refer to
their method
as ITF. They express peculiar velocity as a function of redshift-space,
rather than real-space, position; in the terminology of
SW,
ITF is thus a Method II analysis,
largely impervious to inhomogeneous Malmquist bias.
DNW
expand the redshift-space peculiar velocity field in a set of independent
basis functions, or modes, whose coefficients are solved
for simultaneously with the parameters of a global inverse TF relation
via 
2
minimization of TF residuals. The TF data are never converted into inferred
distances and thus do not require precalibrated TF relations. The
IRAS-predicted velocity field is expanded in the same set of basis
functions, allowing a mode-by-mode comparison of predicted and observed
peculiar velocities. This ensures that one is comparing quantities that
have undergone the same spatial smoothing, a desirable characteristic of
the fit.
As with POTENT, the strengths of ITF are connected with certain disadvantages. Because it is a Method II approach, multivalued or flat zones in the redshift-distance relation (see below) necessarily bias the ITF analysis. It neglects the role of small-scale velocity noise, which is nonnegligible for galaxies within 1000 km s-1. These features make ITF, like POTENT, a relatively ineffective tool for probing the very local region. Last and most importantly, the ITF method as implemented by DNW requires that the raw magnitude and velocity width data from several distinct data sets be carefully matched before being input to the algorithm. Any systematic errors incurred in matching the raw data from different parts of the sky will induce large-scale, systematic errors in the derived velocity field. Thus, although ITF does not need input TF distances, it is vulnerable to a priori calibration errors just as POTENT is.
4 Dekel et al. (1993) and Sigad et al. (1997) actually use a nonlinear extension to eq. (4). Back.