1. INTROUCTION

One of the most important tasks facing observational cosmology is determination of the density parameter . Along with the Hubble constant H₀ and the cosmological constant , the density parameter fixes the global structure of spacetime. One approach to the problem uses the classical cosmological tests of the geometry of the universe, such as the apparent magnitudes as a function of the redshift of standard candles (e.g., Type Ia supernovae; Perlmutter et al. 1997). While promising, this approach is sensitive to the possible evolution of the standard candles with redshift. Moreover, it is difficult to disentangle the effects of and in such tests (Dekel, Burstein, & White 1997a). Alternatively, one may carry out dynamical measurements of in the local (z 0.05) universe, in which both evolution and the geometrical effects of the cosmological constant may be safely neglected.

Low-redshift tests of are based on dynamical measurements of the mass of gravitating matter on some characteristic size scale. For example, measurements of rotation curves (Rubin 1983) or the motions of satellite galaxies (Zaritsky et al. 1993) yield the masses of ordinary spirals within ~ 10-200 kpc of their centers. The velocity dispersions (Carlberg et al. 1996), X-ray temperatures (White, Efstathiou, & Frenk 1993), and gravitational lensing effects (Tyson & Fischer 1995; Squires et al. 1996) of rich clusters of galaxies provide mass estimates on ~ 1 Mpc scales. In general, these and other dynamical analyses of matter in the highly clustered regime have pointed to a mass density corresponding to 0.2 ± 0.1 (e.g., Bahcall, Lubin, & Dorman 1995). This value exceeds that implied by known sources of luminosity (_lum 0.01; Peebles 1993) or inferred from primordial nucleosynthesis (_baryon 0.05; Turner et al. 1996), and thus points to the existence of nonbaryonic dark matter. However, it is well below the Einstein-de Sitter value of = 1 that is favored by simplicity and coincidence arguments (e.g., Dicke 1970). The natural expectation from the inflation scenario is that the universe is flat, + = 1, where / 3H₀² is the effective energy density contributed by a cosmological constant (Guth 1981; Linde 1982; Albrecht & Steinhardt 1982). However, if 0.2, this inflationary prediction requires 0.8, which conflicts with upper limits obtained from studies of gravitational lensing (Carroll, Press, & Turner 1992; Maoz & Rix 1993; Kochanek 1996).

It is possible, however, that could be close to or exactly equal to unity, despite evidence to the contrary from dynamical tests on ~ 1 Mpc scales. This could occur if the dark matter is poorly traced by dense concentrations of luminous matter such as galaxies and galaxy clusters. If so, dynamical tests on scales 10 Mpc are necessary to obtain an unbiased estimate of . Such tests involve measurements of the coherent, large-scale peculiar velocities of galaxies. According to gravitational instability theory (cf. eq. [1]), these motions are related in an -dependent way to the large-scale distribution of mass. If the latter, in turn, can be inferred from the observed distribution of galaxies on large scales, one might hope to derive an estimate of that is free from the pitfalls of small-scale dynamical analyses.

This program requires a comparative analysis of two types of data sets. The first consists of radial velocities and redshift-independent distance estimates for large samples of galaxies. The largest such compilation to date is the Mark III catalog (Willick et al. 1997), which contains distance estimates for ~ 3000 spiral galaxies from the Tully-Fisher (TF; Tully & Fisher 1977) relation and 544 elliptical galaxies from the D_n - relation (Djorgovski & Davis 1987; Dressler et al. 1987). The second type of data set is a full-sky redshift survey with well-understood selection criteria. Several large redshift surveys exist (cf. Strauss & Willick 1995, hereafter SW, and Strauss 1996 for reviews); the one that most nearly meets the requirements of full-sky coverage and well-understood selection is the IRAS 1.2 Jy survey (Fisher et al. 1995). The basic idea behind the comparison is as follows. In the linear regime (mass density fluctuations / ₀ << 1), the global relationship between the peculiar velocity field v(r) and the mass density fluctuation field (r) is given by gravitational instability theory:

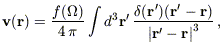
(1)

where f() ^0.6 (Peebles 1980). ⁽¹⁾ If mass density fluctuations are equal to galaxy number density fluctuations, at least on the scales ( few megaparsecs) over which it is possible to define continuous density fields, then the redshift survey data yield a map of (r) (after correction for peculiar velocities; Appendix A). By equation (1), one then derives a predicted peculiar velocity field v(r) as a function of . The TF or D_n - data provide the observed peculiar velocities. The best estimate of is the one for which the predicted and observed peculiar velocities best agree.

Two obstacles make this comparison a difficult one. The first, already alluded to, is fundamental: one observes galaxy number density (_g) rather than mass density () fluctuations. A model is required for relating the first to the second. The simplest approximation is linear biasing,

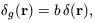
(2)

in which the bias parameter b is assumed to be spatially constant, and no scatter around the relation in equation (2) is assumed. Substituting equation (2) in equation (1) yields

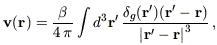
(3)

where f() / b. Thus, under the dual assumptions of linear dynamics and linear biasing, comparisons of peculiar velocity and redshift survey data, by themselves, can yield the parameter but not . One might hope to break the -b degeneracy by generalizing equation (1) to the nonlinear dynamical regime (cf. Dekel 1994, Section 2, or Sahni & Coles 1996 for a review). However, such generalizations are difficult to implement in practice; furthermore, nonlinear extensions to equation (2) will enter in the same order as nonlinear dynamics (we discuss this issue further in Section 6.3.1). Thus, without a more realistic a priori model of the relative distribution of galaxies versus mass, it is prudent to limit the goals of the peculiar velocity-redshift survey comparison to testing gravitational instability theory and determining . One may then adduce external information on the value of b to place constraints on itself.

The second obstacle is the sheer technical difficulty of the problem. The random errors in the redshift-independent distances obtained from methods such as TF are large (~ 20%; Willick et al. 1996) and are subject to potential systematic errors due to statistical bias effects (Dekel 1994; SW, Section 6). Furthermore, we measure the galaxy density field _g in redshift space, whereas it is the real-space density that yields peculiar velocities via equation (3). The relationship between the two depends on the peculiar velocity field itself. Self-consistent methods, in which v_p is both the desired end product and a necessary intermediate ingredient in the calculation, must therefore be developed for predicting peculiar velocities from redshift surveys (Appendix A). For these reasons, reliable comparisons of peculiar velocity and redshift survey data require extremely careful statistical analyses.

This problem has inspired a number of independent approaches in recent years. The POTENT method (Dekel, Bertschinger, & Faber 1990; Dekel 1994; Dekel et al. 1997b) was the first effort at a rigorous treatment of peculiar velocity data. Dekel et al. (1993) compared the POTENT reconstruction of the Mark II peculiar velocity data (D. Burstein 1989, private communication [privately circulated computer files]) to the IRAS 1.936 Jy redshift survey (Strauss et al. 1992b), finding _i = 1.28_-0.59^+0.75 at 95% confidence. ⁽²⁾ An improved treatment using the Mark III peculiar velocities (Willick et al. 1997) and the IRAS 1.2 Jy survey (Fisher et al. 1995) yields _I = 0.86 ± 0.15 (Sigad et al. 1997, hereafter POTIRAS). Hudson et al. (1995) compared the optical redshift survey data of Hudson (1993) with the POTENT reconstruction based on a preliminary version of the Mark III catalog, finding _opt = 0.74 ± 0.13 (1 errors). These results from POTENT were obtained using 1200 km s^-1 Gaussian smoothing. A distinct approach, which differs from POTIRAS in the statistical biases to which it is vulnerable (SW) and which typically uses much smaller smoothing, is to predict galaxy peculiar velocities and thus distances from the density field, and then to use these predictions to minimize the scatter in the TF or D_n - relations (Strauss 1989; Hudson 1994; Roth 1994; Schlegel 1995; Shaya, Peebles, & Tully 1995; Davis, Nusser, & Willick 1996, hereafter DNW). This second kind of analysis has produced estimates of _I in the range ~ 0.4-0.7, lower than the values obtained from POTIRAS. We further clarify the distinction between the two methods in Section 2.1, and discuss possible reasons for the discrepancies in Section 6.1.

In this paper, we present a new maximum likelihood method for comparing TF data with the predicted peculiar velocity and density fields in order to estimate . Its chief strength is an improved treatment of nearby galaxies (cz 3000 km s^-1), and we limit the analysis to this range. The TF data that we use comprise a subset of the Mark III catalog of Willick et al. (1997). The predicted peculiar velocities are obtained using new reconstruction methods (Appendix A) from the IRAS 1.2 Jy redshift survey. ⁽³⁾ The outline of this paper is as follows. In Section 2, we first review the strengths and weaknesses of existing approaches, and then describe our new method in detail. In Section 3, we present tests of the method using mock catalogs. In Section 4, we apply the method to the Mark III catalog and obtain an estimate of _I. In Section 5, we analyze residuals from our maximum likelihood solution in order to assess whether IRAS predictions give a statistically acceptable fit to the Mark III data. In Section 6, we further discuss and summarize our principal results. This paper is the product of nearly 3 years work and contains considerable detail. We recommend that readers interested primarily in results and interpretation skim Section 2, and then read Sections 3.1, 4.4, 4.5, 5.1, 5.2, and 6.4.

¹ We measure distances r in velocity units (km s^-1). In such a system of units, the Hubble constant is equal to unity by definition and does not affect the amplitude of predicted peculiar velocities. Back.

² Because the bias parameter can differ for different galaxy samples, the value of can differ as well. We will use _I for the IRAS redshift survey and _opt for an optical survey. Because optical galaxies are about 30% more clustered than IRAS galaxies (SW), the conversion is _I 1.3_opt. When speaking generically about the velocity-density relation, we will place no subscript on . Back.

³ The original IRAS 1.936 Jy survey was presented in a series of six papers (Strauss et al. 1990; Yahil et al. 1991; Davis, Strauss, & Yahil 1991; Strauss et al. 1992a, 1992b, 1992c), numbered I, II, III, IV, V, and VII, respectively. The missing Paper VI was to be the comparison of the observed and predicted velocities, to be based on Strauss (1989, chap. 3). However, it has taken us until now to come up with statistically rigorous ways of doing this comparison. Thus, the long-lost IRAS Paper VI has been incorporated into Dekel et al. (1993), DNW, Sigad et al. (1997), and especially this paper. Back.