


2.2.3. Implementation of VELMOD
The probability distribution
P(m| ,
cz) (eq. [11]) is dependent on a number of free parameters, most
importantly
,
cz) (eq. [11]) is dependent on a number of free parameters, most
importantly
 I.
However, because
I.
However, because
 I
enters at an earlier stage - in
the reconstruction of the underlying density and velocity fields from
IRAS (Appendix A) - it
is on a different footing from other parameters. Thus, rather than treating
I
enters at an earlier stage - in
the reconstruction of the underlying density and velocity fields from
IRAS (Appendix A) - it
is on a different footing from other parameters. Thus, rather than treating
 I
as a continuous free parameter, VELMOD is run sequentially for the 10
discrete values
I
as a continuous free parameter, VELMOD is run sequentially for the 10
discrete values
 I
= 0.1, ..., 1.0 for the real data, and for the nine discrete values
I
= 0.1, ..., 1.0 for the real data, and for the nine discrete values
 I
= 0.6, ..., 1.4 for the mock catalog data
(Section 3).
(8) For each
I
= 0.6, ..., 1.4 for the mock catalog data
(Section 3).
(8) For each
 I,
the probability is
maximized (
I,
the probability is
maximized ( forw
is minimized) with respect to the remaining free parameters. These
parameters are as follows:
forw
is minimized) with respect to the remaining free parameters. These
parameters are as follows:
 TF
for each sample in the analysis. Here we limit the analysis to the
Mathewson, Ford, & Buchhorn (1992,
hereafter MAT) and
Aaronson et al. (1982a,
hereafter A82)
samples, as we discuss
in Section 4.1. Thus, there are a total
of six TF parameters that are varied. Note that the TF scatters are not
simply calculated a posteriori. The
statistic
TF
for each sample in the analysis. Here we limit the analysis to the
Mathewson, Ford, & Buchhorn (1992,
hereafter MAT) and
Aaronson et al. (1982a,
hereafter A82)
samples, as we discuss
in Section 4.1. Thus, there are a total
of six TF parameters that are varied. Note that the TF scatters are not
simply calculated a posteriori. The
statistic  forw
depends on their values, and they are varied to minimize it.
forw
depends on their values, and they are varied to minimize it.
 v.
The quantities
v.
The quantities  v
and
v
and  TF
can trade off to a certain extent (cf. eq. [15]). However, their
relative importance depends on distance. Sufficiently nearby
(
TF
can trade off to a certain extent (cf. eq. [15]). However, their
relative importance depends on distance. Sufficiently nearby
( 1000 km
s-1),
1000 km
s-1),
 v
is as large or a larger source of error than the TF scatter itself. Thus,
it is determined in this local region. Beyond ~ 2000 km
s-1, the TF scatter dominates the error, and it is determined at
these distances. Because the samples populate a range of distances, the two
can be determined separately, with relatively little covariance.
v
is as large or a larger source of error than the TF scatter itself. Thus,
it is determined in this local region. Beyond ~ 2000 km
s-1, the TF scatter dominates the error, and it is determined at
these distances. Because the samples populate a range of distances, the two
can be determined separately, with relatively little covariance.
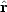 , where
uIRAS(r) is given as described in
Appendix A, and the three Cartesian
components of wLG
are varied in each VELMOD run at a given
, where
uIRAS(r) is given as described in
Appendix A, and the three Cartesian
components of wLG
are varied in each VELMOD run at a given
 I.
We note briefly that this procedure is self-consistent only as long
as |wLG| is at most comparable
to
I.
We note briefly that this procedure is self-consistent only as long
as |wLG| is at most comparable
to  v.
In practice, we will find that
for
v.
In practice, we will find that
for  I
near its best value, the amplitude
of wLG is trivially small.
I
near its best value, the amplitude
of wLG is trivially small.
Thus, there are 3 × 2 + 1 + 3 = 10
free parameters that are varied for any given value of
 I,
when the quadrupole is held fixed. Thus, for any value of
I,
when the quadrupole is held fixed. Thus, for any value of
 I, we
give the data the fairest chance it possibly has to fit the IRAS
model. In particular, the TF relations for the two separate samples used
are not "precalibrated"
in any way. This ensures that TF calibration in no way prejudices the value
of
I, we
give the data the fairest chance it possibly has to fit the IRAS
model. In particular, the TF relations for the two separate samples used
are not "precalibrated"
in any way. This ensures that TF calibration in no way prejudices the value
of  I
we derive.
I
we derive.
8 The
choice of these values of
 I
was based on the need to bracket the "true"
value: 1.0 in the mock catalogs and, as it turns out, ~ 0.5 for
the real data. Back.
I
was based on the need to bracket the "true"
value: 1.0 in the mock catalogs and, as it turns out, ~ 0.5 for
the real data. Back.