2.2.2. Further Discussion of VELMOD Likelihood

The physical meaning of the VELMOD likelihood expressions is clarified by considering them in a suitable limit. If we take _v to be "small," in a sense to be more made precise below, the integrals in equations (11) and (12) may be approximated using standard techniques. In addition, if we neglect sample selection (S = 1) and density variations [n(r) = constant], and assume that the redshift-distance relation is single-valued, we find, for the forward relation,

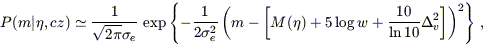
(15)

where w is the solution to the equation cz = w + u(w), i.e., it is the distance inferred from the redshift and peculiar velocity model; _{v v} / [w(1 + u')], where u' = (u / r)_r=w, is the effective logarithmic velocity dispersion; and

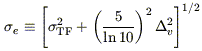
(16)

is the effective TF scatter, including the contribution due to _v. An analogous result holds for the inverse relation. The criterion _v² << 1, which quantifies the statement that _v is "small," must be satisfied to derive equation (15).

Equation (15) shows that the probability distribution P(m|, cz) preserves the Gaussian character of the real-space TF probability distribution P(m|, r) in this limit. However, the expected value of m is shifted from the "naïve" value M() + 5 log w by an amount ~ 4.3_v². This shift is in fact nothing more than the homogeneous Malmquist bias due to small-scale velocity noise; it differs in detail from the usual Malmquist expression (i.e., that which affects a Method I analysis) because it arises from the Gaussian (rather than lognormal) probability distribution (eq. [9]). Furthermore, the effective scatter _e is larger than _TF, because the velocity dispersion introduces additional distance error and thus magnitude scatter. However, the effects associated with velocity noise diminish with distance (_v r^-1); the velocity Malmquist effect vanishes in the limit of large distances, in contrast with the distance-independent Malmquist effect for Method I, and the effective scatter approaches the TF scatter. At large enough distance, the VELMOD likelihood approaches a simple Gaussian TF distribution with expected apparent magnitude M() + 5 log w, and VELMOD reduces to the standard Method II.

Indeed, equation (15) enables us to define the regime in which VELMOD represents a significant modification of Method II. The distance r_II at which the velocity noise effects become unimportant is determined by r_II >> _v / _TF(1 + u'), where _TF = ln10_TF/5 is the fractional distance error due to the TF scatter (_TF 0.2 for the samples used here). For _v = 125 km s^-1, the value we find for the real data (Section 4.5), this shows that in the unperturbed Hubble flow, where u' = 0, velocity noise effects become unimportant beyond ~ 1500 km s^-1. However, at about this distance, in many directions, the Local Supercluster significantly retards the Hubble flow, u' -0.5, so that the effective _v is about twice its nominal value. Thus, VELMOD in fact differs substantially from Method II to roughly twice the Virgo distance. This fact guided our decision to apply VELMOD only out to 3000 km s^-1 (cf. Section 4).

Equation (15) also demonstrates that maximizing the likelihood (minimizing _forw) is not equivalent to ² minimization, even under the adopted assumptions of constant density and negligible selection effects, because of the factor _e^-1 in front of the exponential factor. This factor couples the velocity model [i.e., the values of w and u'(w)] to the velocity noise. In particular, maximizing the VELMOD likelihood is not equivalent to minimizing TF scatter (cf. Section 4.5), except in the limit that _v is set to zero.

The assumptions required for deriving equation (15) remind us that there are two other factors that distinguish VELMOD from standard Method II. First, for realistic samples one cannot assume that S = 1. The presence of the selection function in equations (6) and (7) is essential for evaluating true likelihoods, and we have fully incorporated these effects into our analysis. ⁽⁷⁾ Second, the galaxy density n(r) is not effectively constant along most lines of sight. Thus, VELMOD, like Method I but unlike Method II, requires that n(r) be modeled. We do so here by using the IRAS density field itself, which is a good approximation to the number density of the spiral galaxies in the TF samples. The density field has a nonnegligible effect on the VELMOD likelihood whenever it changes rapidly on the scale of the effective velocity dispersion _v / (1 + u').

The most significant differences between VELMOD and Method II thus occur in regions where u' - 1 (flat or triple-valued zones), or when the density varies particularly sharply. In practice, both these effects occur in the vicinity of large density enhancements such as the Virgo Cluster. We illustrate this in Figure 1, which shows the redshift-distance relation and the corresponding value of P(r|cz) P(cz|r)P(r) in the vicinity of triple-valued zones. When looking at these panels, keep in mind that the VELMOD likelihood is given by multiplying P(r|cz) and the TF probability factor P(m|, r) and integrating over the entire line of sight. Figures 1a and 1b depict the situation near the core of a strong cluster, and Figures 1c and 1d depict it farther from the center. In each case, the cloud of points represents the velocity noise, here taken to be _v = 150 km s^-1. In Figure 1a, the redshift of 1200 km s^-1 crosses the redshift-distance diagram at three distinct distances. The quantity P(r|cz) shows three distinct peaks. The highest redshift one is the strongest because of the r² weighting in equation (8). In Figure 1b, the redshift of 1700 km s^-1 is such that the object just misses being triple-valued; however, the finite scatter in the redshift-distance diagram means that there is still appreciable probability that the galaxy is associated with the near crossing at cz ~ 900 km s^-1. In Figure 1c, the redshift-distance diagram goes nearly flat for almost 600 km s^-1; a redshift that comes close to that flat zone has a probability distribution that is quite extended. Finally, Figure 1d shows a galaxy whose redshift crosses the redshift-distance diagram in a region in which it is quite linear, and the probability distribution has a single, narrow peak without extensive tails.

Figure 1. Effects of triple-valued or flat zones. The S-shaped curves show the relation between redshift and distance along two lines of sight to a cluster. (a) A galaxy with a redshift of 1200 km s-1 can lie at three distinct distances. When the small-scale noise inherent in any velocity field model, as indicated by the scattered points, is taken into account, the quantity P(r|cz), shown as the three-peaked curve at the bottom, gets smoothed out. (b) A galaxy at 1700 km s-1 along the same line of sight intersects the redshift-distance curve at only one point but comes close enough to it elsewhere to give a second peak to the P(r|cz) curve. (c) Farther from the cluster, the redshift-distance curve becomes flat, giving a broad peak to P(r|cz). (d) At a redshift sufficiently far from a triple-valued zone, P(r|cz) has only one narrow peak.

Two final details deserve brief mention. First, the integrals over m and that appear in the denominators of equations (11) and (12) may be done analytically for the case of "one-catalog selection" studied by Willick (1994, Section 4.1), which indeed applies for the samples used in this paper (Willick et al. 1996). The numerical integrations required to evaluate equations (11) and (12) are thus one dimensional only. Second, as noted above, the velocity width distribution function () drops out of equation (11), but the luminosity function (M) does not drop out of equation (12) Thus, inverse VELMOD requires that we model the luminosity function of TF galaxies. This is an annoyance at best and could introduce biases, if we model it incorrectly, at worst. Thus, we have chosen to implement only forward VELMOD in this paper. On the other hand, inverse VELMOD enjoys the virtue that inverse Method II approaches do generally: to the degree that the selection function S is independent of and r, it drops out of equation (12). In a future paper, we will apply the small-_v approximation to VELMOD for more extensive samples to larger distances. For that analysis, the inverse approach will be used as well.

⁷ Selection effects are not specific to VELMOD per se, however. They can and should be modeled in any Method II-like analysis. In particular, they do not vanish in the _v 0 limit. Back.