5.2. Residual Autocorrelation Function

The sky plots shown above provide visual evidence that the _I = 0.5 plus quadrupole fit has small residuals generally, although they are correlated to some degree. In this section, we quantify these correlations with the residual autocorrelation function,

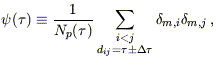
(25)

where _m was defined in equation (23) and the sum is over the N_p() distinct pairs with IRAS-predicted separation d_ij within = 100 km s^-1 of a given value . This definition makes () insensitive to the values of _TF and _v (because the _m,i are themselves normalized using their maximum likelihood values for each _I), but sensitive to the residual correlations that signal a poor fit.

In Figure 17, we plot () versus for the IRAS plus quadrupole models, with _I = 0.5, 0.1, and 1.0, as well as the _I = 0.6, no-quadrupole model. The error bars are described below. The model that fits best according to the likelihood statistic, _I = 0.5 plus quadrupole, shows no significant residual correlations on any scale. The correlation function is everywhere consistent with zero, as we would expect if the IRAS velocity field plus the quadrupole is indeed a good fit to the data. Indeed, the absence of residual correlations is the basis for a statement made in Section 2.2.1, namely, that the individual galaxy probabilities P(m, cz) are independent, and thus validates the VELMOD likelihood statistic _forw.

Figure 17. VELMOD residual autocorrelation functions, (), plotted for I = 0.5 plus quadrupole (best-fit model), I = 0.6 no quadrupole, I = 0.1 plus quadrupole, and I = 1.0 plus quadrupole. In the I = 0.1, several points at large have residuals that are so large that they fall beyond the plot boundaries.

The other models shown in Figure 17 all exhibit significant residual correlations. The _I = 0.6, no-quadrupole model has noticeable correlations on small and large scales, as does the _I = 0.1 plus quadrupole model. Indeed, several of the values of () for _I = 0.1 are so large that they are off-scale on the plot. The _I = 1.0 plus quadrupole model exhibits strong correlations for 2000 km s^-1, although it is well behaved on large scales.