Annu. Rev. Astron. Astrophys. 1998. 36: 599-654 Copyright © 1998 by Annual Reviews. All rights reserved

2.2. Gas Dynamics

The first cosmological simulations with gas dynamics were one-dimensional, plane-parallel treatments of gas and dark matter flows in the sheet-like caustics ("Zel'dovich pancakes") that form as the first nonlinear structures in models with purely large-scale initial density fluctuations (e.g. Doroshkevich et al 1978). Shapiro et al (1983), Bond et al (1984) modeled the combined growth of baryon-neutrino pancakes in a universe dominated by massive neutrinos, showing that only a small fraction of the baryons would be able to cool in the postshock regions of these pancakes. In one dimension, even these early simulations were able to include detailed treatments of ionization, recombination, radiative and Compton cooling, and thermal conductivity (Shapiro & Struck-Marcell 1985).

The strong nonlinearity of the gas dynamical equations, manifested in the ubiquity of oblique shock waves in cosmological simulations, makes it difficult or impossible to develop numerical methods whose accuracy and convergence can be proven. Computational gas dynamics is art more than science. For this reason, testing of algorithms against simple (one-dimensional) problems with exact solutions, as well as comparison of different codes against each other, is essential to proving their validity. A comparison of several cosmological gas dynamics codes was performed by Kang et al (1994); a more extensive project is underway currently by Frenk et al (CS Frenk, SDM White, P Bode, JR Bond, GL Bryan, et al, unpublished manuscript).

In comoving coordinates, the cosmological fluid equations are

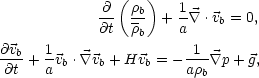(3)

where _b, _b, _b, and p are the (baryonic) mass density, mean mass density, peculiar velocity, and pressure, respectively, and 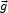is the gravitational field (Equation 1). These must be supplemented by either an energy or entropy equation. Outside of shocks, these take the form

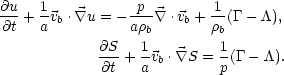(4)

For a perfect gas with ratio of specific heats , the thermal energy and entropy per unit mass are u = p / [( - 1) _b] and S = ( - 1)^-1 ln (p _b^-), respectively. Artificial viscosity is often added to Equation 4 to generate the entropy needed across shock waves. In nonadiabatic calculations, heating and cooling rates per unit volume and and all they depend on, such as ionization and chemistry rate equations, radiative transfer, etc, must be included.

2.2.1. SMOOTH-PARTICLE HYDRODYNAMICS    Smooth-particle hydrodynamics (SPH) is a Lagrangian (particle-tracking) method for integrating the fluid equations invented by Lucy (1977), Gingold & Monaghan (1977). The fluid variables (baryon density, velocity, temperature, etc) are followed using particles of fixed mass representing fluid elements. The method is therefore an extension of N-body methods, making it relatively easy to add SPH to existing cosmological simulation codes. SPH has been reviewed by Monaghan (1992).

The first cosmological SPH codes were written by Evrard (1988), who combined gas dynamics with a P³M code, and by Hernquist & Katz (1989), who based their SPH on a tree code (see also Katz et al 1996a). Since then, many other groups have added SPH to cosmological simulation codes (Thomas & Couchman 1992, Steinmetz & Müller 1993, Couchman et al 1995, Serna et al 1996, Shapiro et al 1996, Steinmetz 1996, Tissera et al 1997). Recently, several parallel implementations have been developed (Pearce & Couchman 1997, Davé et al 1997a, Nakasato et al 1997).

Because SPH is Lagrangian, the mass continuity equation (the first of Equation 3) is obviated. The baryonic mass density is estimated by treating each particle as spread out with a smoothing kernel W:

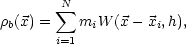(5)

where m_i and _i are, respectively, the particle mass and position, and h is a smoothing length. A kernel of compact support such as a spline is used so that the sum extends only over particles closer than some cutoff radius proportional to h. These particles are easily found from neighbor lists constructed with the tree or P³M algorithms. The smoothing length generally is taken to vary with _b^-1/3 so that a fixed number of particles (typically 30-40) is included in the kernel sum. Numerical issues associated with variable smoothing length have been discussed by many authors, including Hernquist (1993), Steinmetz & Müller (1993), Serna et al (1996). A stability analysis has been performed by Balsara (1995), who provided suggestions for optimal parameters. The resolution of SPH has been improved significantly by Shapiro et al (1996) by using an adaptive ellipsoidal rather than spherical smoothing kernel and by switching off artificial viscosity for all particles except those that are in or about to enter shocks. Navarro & Steinmetz (1997) have also found improvements after reducing the amount of artificial shear viscosity.

The accuracy of SPH is more difficult to assess than for Eulerian (fixed-grid) hydrodynamics algorithms because of the absence of any rigorous proof of convergence to the solutions of the fluid equations in the continuum limit. Comparisons with other algorithms (e.g. Kang et al 1994) suggest that while SPH allows for very high-density contrasts, it suffers from poor resolution of shocks as well as low resolution in low-density regions. Nonetheless, its relative ease of implementation, combined with its high resolution in dense regions, makes SPH an excellent practical method for cosmological gas dynamics.

2.2.2. EULERIAN GRID ALGORITHMS    Finite-difference methods have long been used to provide numerical approximations of the Eulerian fluid equations for computational fluid dynamics (Richtmeyer & Morton 1967). Cosmological gas flows are often highly supersonic; the gas falling into clusters of galaxies is shock-heated from 10⁴ to 10⁸ K. Robust schemes are needed to ensure the correct treatment of shocks and other discontinuities (e.g. contact discontinuities, across which the density and temperature jump but not the pressure, and tangential discontinuities, across which the tangential velocity changes). A variety of reliable methods have been developed and tested extensively in the computational fluid dynamics community (e.g. Sod 1985, LeVeque 1992).

The first multidimensional applications of these methods to cosmology, using artificial viscosity for the treatment of shocks, were made by Ryu et al (1990), Cen et al (1990), Yuan et al (1991). Ryu et al used the multidimensional flux-corrected transport method (Sod 1985). Cen et al used an approach developed in aeronautical engineering by Jameson (1989) and detailed by Cen (1992). Yuan et al used ZEUS-2D, a radiation-magnetohydrodynamics code developed by Stone & Norman (1992), with modifications described by Anninos & Norman (1994). All of these early cosmological gas dynamics codes were robust and performed reasonably well on simple tests. However, they did not resolve shocks as well as modern shock-capturing methods based on solution of the Riemann problem for the evolution of fluid discontinuities (Landau & Lifshitz 1959) without explicit artificial viscosity (e.g. LeVeque 1992). Hence efforts have shifted to the implementation of newer algorithms.

Two approaches have been used for high-resolution shock-capturing algorithms in cosmology: total-variation diminishing (TVD) schemes and the piecewise parabolic method (PPM). In both schemes, the gas dynamical equations are written in conservation law form, i.e. uⁱ / t + ( / x^j) F^ij(u) = 0, where uⁱ is a vector of densities (mass, momentum, and energy) and F^ij is a vector of fluxes for these densities. Fluxes are computed across cell boundaries to update the cell-average densities. Terms such as cosmological expansion, heating and cooling, and gravity may be included as source terms using the method of operator splitting with fractional timesteps (Richtmeyer & Morton 1967).

In TVD schemes, the fluxes are computed using an approximate solution of the Riemann problem, with corrections added to ensure that there are no postshock oscillations. The TVD codes of Ryu et al (1993), Quilis et al (1994, 1996) are "second-order" accurate away from shocks, meaning that as the mesh spacing is reduced by a factor f, the numerical truncation errors go down by a factor f². More importantly, perhaps, they resolve shock jumps correctly in just two grid zones.

The PPM algorithm (Collela & Woodward 1984, Woodward & Collela 1984) is a third-order accurate extension of the Godunov method (LeVeque 1992). The Riemann problem at cell boundaries is solved accurately using a quadratic interpolation of the cell-average densities that is constrained to minimize (but not entirely eliminate, unlike TVD) postshock oscillations. Away from shocks, PPM is third-order accurate. Shocks are resolved slightly better than in lower-order TVD codes. PPM has been implemented in cosmology by Bryan et al (1995), Sornborger et al (1997).

2.2.3. ADAPTIVE GRID ALGORITHMS    Eulerian methods give the most accurate solution of the gas dynamical equations for a given resolution, but they suffer from the resolution limit of the grid. Current simulations generally use at most 512³ grid cells (with a few heroic runs of larger size on parallel machines), whereas cosmologists need a spatial dynamic range of 10⁴ or more to follow galaxy formation. Two variations of grid-based hydrodynamics have been employed to increase the resolution: mesh refinement and deformable moving meshes.

Mesh refinement is discussed above in the context of solving the Poisson equation (Sections 2.1.3 and 2.1.4). Such methods have been used for more than a decade in computational fluid dynamics. Their first application to cosmological gas dynamics was made by Anninos et al (1994), who used a two-level hierarchy of cubic grids for solving the fluid equations with higher resolution in an interesting simulation subvolume. The subvolume was taken to be fixed in space and present throughout the simulation, and a three-dimensional implementation of the ZEUS code with second-order accurate fluxes was used for the gas dynamics solver. Their method was a first step toward fully adaptive mesh refinement in which refinement grids are placed (and removed) dynamically at multiple levels of refinement where needed during the course of a simulation. With PPM as the gas solver, adaptive mesh refinement has recently been demonstrated by Bryan & Norman (GL Bryan & ML Norman, unpublished manuscript, astro-ph/9710187). They achieved a peak dynamic range of 8192³ using grids of size 64³ or less. Their method is very promising for future high-resolution studies of cosmological gas dynamics.

An alternative approach to higher resolution is to allow the mesh to deform with the flow. Gnedin (1995) has developed a moving mesh hydrodynamics solver in which the grid locally expands and contracts so as to approximately track the flow of gas without the grid crossing itself. Such methods may offer the advantages of both SPH (high resolution owing to its Lagrangian nature) and Eulerian codes (shock capturing in two grid zones), although severe mesh distortion leads to new errors that need further study.

2.2.4. OTHER GAS DYNAMICS ALGORITHMS    Several other algorithms have been used for approximate or phenomenological treatments of cosmological gas dynamics. One early approach was the method of "sticky particles" in N-body codes, whereby particles labeled as gaseous are allowed to collide inelastically when sufficiently close. Based on the local density and temperature estimated from the pair separation and relative velocity, the colliding pair may be merged together (Blumenthal et al 1986). Alternatively, the relative kinetic energy may be dissipated and the gas particles converted into "stars" (i.e. made collisionless) at sufficiently high density (Carlberg 1988a, b, Carlberg & Couchman 1989). A more sophisticated approach is the "beam scheme" in which the gas is represented by sampling the microscopic Maxwellian velocity distribution at several discrete values in each cell of the simulation volume. Mass, momentum, and energy are transported according to kinetic theory (Sanders & Prendergast 1974). This method has been applied in cosmological simulations by Vishniac et al (1985), Chiang et al (1989); compared with Eulerian finite-difference methods, it has relatively large numerical viscosity. A still more sophisticated method, based on gas kinetic theory applied on an unstructured mesh, has been used by Xu (1997). In one-dimensional simulations, Xu's method resolves shocks in about two mesh cells.