Annu. Rev. Astron. Astrophys. 1998. 36: 599-654 Copyright © 1998 by Annual Reviews. All rights reserved

3.3. Velocity Statistics

The spatial statistics listed above make use of only half the phase space coordinates of particles, neglecting velocity information (or, in redshift space, using radial velocity in place of distance). Although it is difficult to measure sufficiently accurate extragalactic distances to obtain reliable peculiar velocities (Strauss & Willick 1995), different cosmological models vary substantially in their predictions (especially as a function of the density parameter ), making investigation of peculiar velocities well worthwhile.

The simplest velocity statistic is the velocity distribution of single particles, f(v)4 v² dv where v is the magnitude of peculiar velocity. This statistic is poorly studied despite the fact that it is the lowest-order distribution function appearing in the BBGKY kinetic theory of gravitational clustering (Peebles 1980). Either the radial component or one Cartesian component may be used instead of the magnitude of the three-dimensional velocity; because of isotropy, all three distributions are simply related. Inagaki et al (1992), Raychaudhury & Saslaw (1996) compared the predictions of the thermodynamic theory of Saslaw & Hamilton (1984) with simulations starting from Poisson initial conditions, and they found good agreement. Cen & Ostriker (1993c) examined f(v) for galaxies formed in their CDM simulations and noted that an exponential distribution fits better than a Maxwellian.

Davis et al (1997) have proposed using the small-scale velocity dispersion ₁, the second moment of f(v) after filtering out long-wavelength velocity contributions, to provide an estimate of through the Layzer-Irvine cosmic energy equation. In practice, they measure this single-particle dispersion using a single-particle weighting of a pairwise velocity. This statistic has the advantage of being less sensitive to sampling fluctuations from clusters of galaxies than the pair-weighted pairwise velocity dispersion (e.g. Zurek et al 1994, Somerville et al 1997). Alternatively, a redshift dispersion may be measured as a function of density, as suggested by Kepner et al (1997b).

Besides examining the velocities of individual particles or galaxies, study is possible of the "fluid" or "bulk flow" velocity obtained by averaging the velocity over a window of radius R, 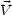(R). Kofman et al (1994) showed analytically and with N-body simulations that in the mildly nonlinear regime, the distribution of 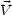remains close to Maxwellian for Gaussian initial conditions. The steep decline of the Maxwellian for bulk flows that are much larger than the rms leads to a sensitive test of power on large scales (e.g. White et al 1987b, Bertschinger & Juszkiewicz 1988). Other velocity field statistics include the cosmic Mach number = V(R) / (R), where (R) is the small-scale velocity dispersion within the same window (Ostriker & Suto 1990). Bulk flows are sensitive to large-scale power, while small-scale dispersions are sensitive to smaller scales, so is sensitive to the shape of the power spectrum.

Another statistic applied to the large-scale velocity field is the distribution of velocity divergence, f () d where = ^. (Bernardeau 1994). The velocity divergence is attractive theoretically because in the linear regime, it is proportional to the density fluctuation (see Equations 6 and 7); in the mildly nonlinear regime for Gaussian initial conditions, the ratio of its skewness to the square of its variance is sensitive to (Bernardeau et al 1995, 1997); and for a potential flow (as expected on large scales for gravitationally induced motions), the velocity field is fully described by () (Bertschinger & Dekel 1989).

The statistics of relative velocities of pairs of galaxies have been extensively studied on small scales because of the possibility of measuring using the cosmic virial theorem (Peebles 1980), which relates these velocities to the two- and three-point correlation functions. The relative velocity of a pair separated by , ₁ - ₂ , is decomposed into a component along and the remainder perpendicular to it. The distribution of v₁₂ ^. (₁ - ₂) , in particular its mean <v₁₂> and standard deviation ₁₂, has been studied extensively in numerical simulations, initially by Davis et al (1985) and more recently by others, including Zurek et al (1994), Gelb & Bertschinger (1994b), Brainerd et al (1996), Colin et al (1997). The sensitivity of ₁₂ to rich clusters makes it difficult to measure well but also provides discriminating power among different structure formation models (Somerville et al 1997). Sheth (1996) recently has provided analytical insight into the exponential form of f(v₁₂) by using an extension of the Press-Schechter theory (Press & Schechter 1974; cf also Mo et al 1996).