Annu. Rev. Astron. Astrophys. 1998. 36: 599-654 Copyright © 1998 by Annual Reviews. All rights reserved

3.4. Redshift Space Distortions

A few words may be said here about both the challenges and opportunities afforded by the "redshift space distortions" arising when redshift is used in place of distance. The effects of peculiar velocities on the two-point correlation function have been extensively studied with simulations (e.g. Suto & Suginohara 1991, Bahcall et al 1993, Matsubara 1994). To characterize these effects, it is useful to distinguish redshift differences along the line of sight () and perpendicular to it (r_p), leading to the two-dimensional correlation function (r_p, ) (Davis & Peebles 1983). The effects of peculiar velocities on the power spectrum were first investigated analytically by Kaiser (1987), who showed that the anisotropy of P_s(k, µ) (where cos^-1 µ is the angle between 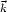and the line of sight) in the quasilinear regime (i.e. on large scales) depends simply on f() / b ^0.6 / b, where b is the linear bias parameter. This effect has been studied thoroughly in simulations (e.g. Bahcall et al 1993, Cole et al 1995, Brainerd et al 1996). The measured spectrum contains information about both the spatial clustering and ; both are important to obtain from redshift surveys. Gramann et al (1994) have explored means of undoing the redshift space distortion on large scales to recover the real-space density. Cole et al (1994) focused instead on practical determination of .