3. THE CIB and CRB INTENSITIES PRODUCED BY STAR-FORMING GALAXIES

The specific intensity I^crb(_R) of the CRB at the observed radio frequency _R is given by the integral over sources (e.g. Peebles 1993):

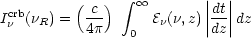(4)

where (, z) is the specific radio luminosity per comoving volume element at redshift z, = _R(1 + z) is the frequency in the rest frame of the luminous objects and |dt / dz| is given by (Hogg 1999)

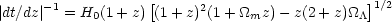(5)

where H₀ is the Hubble constant, h its value in units of 100 km s^-1 Mpc^-1, _{m m} / _c is the present mass density of the universe normalized to the critical density _c = 1.88 × 10^-29 h² g cm^-3, and / 3H²₀ is the dimensionless cosmological constant.

We will assume that the radio-IR correlation, expressed at a given rest frame frequency ₀, holds for all redshifts and that the radio spectrum of the individual galaxies follows a ~ ^- power law with spectral index , so that P(, L_IR, z) = ( / ₀)^- P(₀, L_IR, z). The spectral luminosity density can then be expressed as:

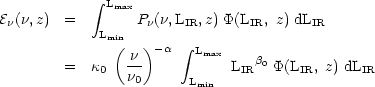(6)

where (L_IR, z) [d(L_IR, z) / dL_IR] is the differential IR luminosity function, d(L_IR, z) is the comoving number density of galaxies with luminosities between L_IR and L_IR + dL_IR in the {L_min, L_max} luminosity interval, and ₀, ₀ are the parameters of the radio-IR correlation at frequency ₀.

The specific intensity of the CRB can now be written as:

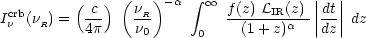(7)

where _IR(z) is the comoving IR luminosity density at redshift z:

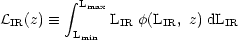(8)

and f (z) is defined as:

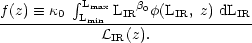(9)

The same star forming galaxies give rise to the CIB with an intensity I_CIB that is given by:

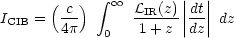(10)

For a linear correlation, ₀ = 1, and f (z) = ₀(Hz^-1). The spectral intensity of the CRB then becomes:

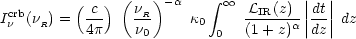(11)

In this case the relation between I^crb_R and I_CIB is considerably simplified and given by:

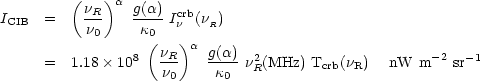(12)

where

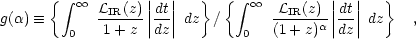(13)

and T_crb(_R) is the CRB brightness temperature at frequency _R.