Annu. Rev. Astron. Astrophys. 1988. 36: 539-598 Copyright © 1998 by Annual Reviews. All rights reserved

3.3. Nonlinear Ejection Models

Analytical solutions for the acceleration of jets from disks and magnetospheres around black holes are limited in their applicability. A time-dependent three-dimensional (3-D) analysis is required to explore the onset and evolution of the physical effects beyond the linear level. For this we can use numerical simulations, taking into account that numerical solutions are a valid approximation of the exact solutions, provided conditions of resolution, stability, and accuracy of the discrete integration domain are fulfilled. In general, these conditions are not known a priori, so testing and verification procedures are an essential part of modeling.

The equations of compressible fluid dynamics are coupled nonlinear, multidimensional, partial differential equations. They are transformed into a linear system of equations by a finite difference scheme and solved by adopting implicit or explicit algorithms with appropriate choices of grids. The treatment of dissipation terms governing the formation of shocks and discontinuities is the crucial point. Classical methods (e.g. Lax-Wendroff) were based on adopting dissipation terms in linear approximation (artificial viscosity) so that the same amount is applied to all grid points. In hybrid methods (e.g. flux-corrected transport, FCT), numerical dissipation is nonlinear, as a high-order, more dissipative approximation is used in smooth regions of the flow and a low-order, less dissipative approximation near discontinuities. The most robust method for treating shocks is the Godunov method, adopted for instance in the Parabolic Piecewise Method (PPM) code, based on an upwind differentiation in the direction of characteristics; cells are considered to be uniform states, and a standard Riemann problem for the nonlinear waves is solved across the interfaces. A different algorithm is used in Smoothed Particle Hydrodynamics (SPH), based on treating cells as particles interacting via collisional terms.

Fluid simulations of accretion disks and supersonic jets are rather cumbersome because large integration domains are necessary to test whether evolutionary patterns are transient or correspond to stationary configurations before they hit the domain boundaries. This limits the number of spatial dimensions that can be used; only massive supercomputers allow fully 3-D simulations. More often, computations are done in 2-D or 2.5-D dimensions (including the third coordinate for vector components but in 2-D symmetry) and therefore completely miss nonaxisymmetric modes that are known to be important.

Finally, hydrodynamic models are simpler than MHD models, but the origin of acceleration goes back to ad hoc mechanisms such as radiation or thermal pressure. Maxwell equations increase the number of characteristics in the fluid system and make the numerical solutions more unstable. On the other hand, magnetic fields are essential in disk/jet modeling, and their correct representation is extremely important. In the following section, we discuss only MHD simulations, even though the existing numerical codes still have limited accuracy.

SWEEPING MAGNETIC TWIST    The first attempt to study the time-dependent nonlinear magnetic disk/jet structure evolution was made by Uchida & Shibata (Uchida & Shibata 1985, Shibata & Uchida 1986), who solved an initial value problem in axisymmetric geometry using a Lax-Wendroff numerical scheme. More recently, these results have been extended to the complete 3-D geometry (Shibata & Uchida 1990) and to general relativistic conditions (Koide et al 1998). They assumed the existence of a geometrically cold thin disk with (v_s / v_K)² 10^-2 rotating around a point mass at Keplerian or sub-Keplerian azimuthal velocities (v / v_K = 0.6-1.0), and they used ideal MHD equations in cylindrical geometry (r, , z). In their model, a uniform magnetic field such that (v_A / v_K)² = 10^-2-10^-3 penetrates the disk vertically, and a nonrotating corona is present outside the disk. The rotating disk bends the poloidal magnetic lines and develops a toroidal structure. The buildup of magnetic tension in the disk is released along the poloidal lines as large-amplitude torsional Alfvèn waves (sweeping magnetic twist). This process extracts angular momentum from the disk that starts collapsing toward the center: When the toroidal field has become strong enough, mass is ejected along the poloidal lines and gives rise to a hollow jet structure. The acceleration of the jet matter is essentially due to the J × B and centrifugal forces. The final magnetic configuration has a poloidal field in the form of an hourglass with a helical toroidal annulus moving axially at the local Alfvèn speed. In the jet, this local speed becomes greater than the Keplerian velocity; thus ejection velocities are a few times v_K . In the general relativistic version of the model, a fast flow, close to the rotation axis and confined by the hollow slow flow, is accelerated up to v_j ~ 0.9 c or _j ~ 2. The process applies to both Keplerian and sub-Keplerian disks, but the latter evolve faster and give rise to more vigorous jets. Near the disk the collimation of the jet is due to the poloidal field, while farther out the toroidal field pinches the outflow in the axial direction.

The Uchida & Shibata model deals with the disk in a fully dynamical way, including the response of the disk to the ejection of jets. However, the link between the two components is related to the mechanism of "numerical" magnetic field reconnection in the inner part of the disk, from where toroidal magnetic flux is ejected along poloidal field lines. The Lax-Wendroff scheme is highly dissipative and does not allow excessive enhancements of the toroidal field that could lead to disruption of the configuration.

Stone et al (1994), using a PPM code, extended the above results to the low magnetic field regime. In this regime, the dynamo process enhancing the disk magnetic field corresponds to the Balbus & Hawley's (1991) magneto-rotational instability. In fact, generation of enhanced accretion onto the central black hole can be observed as a result of the extraction of angular momentum by the Alfvèn torsional waves that arise from the instability.

More recently, the back-reaction of the jet formation has been studied by Matsumoto et al (1996) by referring to geometrically thick disks in axisymmetric conditions. Their results are very similar to those obtained for thin disks, but here the accretion avalanche can actually be seen to occur at the surface of the disks where torsional Alfvèn waves accelerate jets and remove angular momentum. Again, a crucial point is the detailed dynamical behavior at the inner edge of the disk. The accretion flows pulling the magnetic field from the upper and lower surfaces of the disk meet at the tip of the disk with opposite magnetic polarities. Magnetic reconnection may take place and may be used to produce nonthermal particles (see Section 6).

Whether the sweeping twist mechanism can reach a stationary configuration remains an open question. A condition for stationary inflow/outflow is the continuous supply of matter and magnetic field to the disk corresponding to the steady output of power along the jet by the Poynting flux of the torsional Alfvèn waves.

STATIONARY OUTFLOWS    Romanova et al (1997) aimed to find stationary solutions. They assumed that an outflow originates from a disk that is considered as a fixed boundary condition; the initial magnetic field is taken to be a tapered monopole field. Matter is pushed out of the accretion disk with a velocity that is less than the slow magnetosonic velocity. It is then accelerated through the three MHD critical points and reaches a super-fast magnetosonic final velocity. Acceleration occurs especially in the innermost part of the system where the magnetic field is strong. These solutions do not show collimation at large distances, as the kinetic energy density prevails over the magnetic one. In contrast, according to Ustyugova et al (1995), stationary solutions are not possible for = v_s² / v_A² >> 1. In that limit, the rotation of the disk generates a strong toroidal field that pinches the outflow, as in the sweeping twist.

Ouyed & Pudritz (1997a) have presented 2.5-D time-dependent simulations of the evolution of nonrelativistic outflows from Keplerian disks steadily orbiting a central point mass that is accreting at sub-Eddington rates. They used an extended version of the ZEUS-2D code (see next section). The disk is treated as a fixed boundary with a cold corona in stable equilibrium that is supported by Alfvènic turbulent pressure, most likely generated by the Balbus-Hawley instability (Balbus & Hawley 1991). The initial magnetic field configuration in the corona is a poloidal potential field (J = 0), smoothly connected with a toroidal magnetic field in the disk that scales as B 1 / r. Gas is injected from the disk at very low speed into the corona (v_z = 10^-3 v_K), where magnetic lines are opened to more than the critical angle for centrifugal acceleration through the Alfvèn and fast magnetosonic points and collimation in cylindrical structures parallel to the rotation axis. This collimation is due to the pinching force of the toroidal field that is self-consistently generated by the outflow dynamics (currents flow primarily along the axis); these results agree with the Heyvaerts & Norman's (1989) asymptotic analytic solutions. Stationary solutions are found for the adopted set of model parameters, in particular for relatively strong magnetic fields, with = 1 at the innermost radius of the disk. The jet axial velocity v_z is a few times the Keplerian velocity at the fast magnetosonic point and then increases z, as is expected theoretically from hydrodynamic models (Raga & Kofman 1992). A large fraction of the energy in the jet is in the poloidal kinetic energy (two thirds of the total), the rest in toroidal magnetic energy.

Meier et al (1997) have performed an extended analysis of the parameters space of time-dependent numerical simulations of the outflow induced by the corona of magnetized accretion disks, starting from axisymmetric configurations that are consistent with the Blandford & Payne analytical model. The strength of the magnetic field used in their simulations can be much higher than in most other simulations. They assumed a thin cold dense disk with a tenuous hot corona (but with temperature less than the virial halo that permeates the system); initially, magnetic field lines are purely poloidal (B = 0) and are anchored in the disk and protrude into the corona at an angle 60° with respect to the disk. The resulting outflow is collimated into a jet in all cases, but its dynamical characteristics depend on the ratio = v_A / v_esc, where v_A is the Alfvèn velocity in the corona and v_esc = (2GM_h / R)^1/2 the escape velocity. For 1, gravitational forces dominate over magnetic forces, and the jet is accelerated by an upward recoil due to an increase of the disk magnetic field by differential rotation. This acceleration has low efficiency and the final velocities are below v_esc. For 1, the jet is produced by magneto-centrifugal acceleration and is collimated by an azimuthal field; the final velocities are typically v_j 10v_esc for v_A of the order of the Keplerian velocity at the inner radius of the disk and increase further for increasing v_A. The transition between the two modes of jets is rather sharp, and the authors use the term "magnetic switch": For small fields, the jet transports essentially magnetic energy in the advected magnetic field, and for large fields, the jet carries a significant amount of kinetic energy. The transferred energy does not show any switch in total power, and in either form, it is available for particle acceleration and radiation. Figure 4 shows the jet speed as a function of the coronal field strength and also includes results from simulations by other authors.

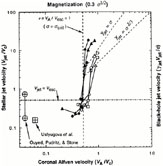Figure 4. Numerical jet simulations from Meier et al (1997).

Meier et al (1997) suggest a possible correlation of weakly magnetized outflows with FR I jets and of highly magnetized ones with FR II jets. Their simulations are easily extended to the special relativistic case and show that current wind theories break down for low magnetic fields, as, in this regime, gravitational effects that are generally neglected become important. The bulk Lorentz factor of highly magnetized solutions can be as large as _j 10.

EPISODIC OUTBURSTS    Observations show that the brightness distribution in jets is very knotty, beginning at VLBI scales. In addition, short time-scale variabilities in blazars may be due to irregularities in the associated jets. Therefore, nonstationary outflow solutions are also interesting for modeling extragalactic jets.

Ouyed & Pudritz (1997b) applied their model to analyze the influence of the magnetic topology on the solutions and in fact have solved the case of bursting outflows. From the original Blandford & Payne analytic solution, it was clear that centrifugally driven winds are not possible if the poloidal magnetic lines are not open to an angle 60° to the disk. Therefore, in a configuration where the initial lines are parallel to the rotation axis, the formation of winds is not expected. In reality, the progressive winding of magnetic lines in the disk generates large-amplitude nonlinear torsional Alfvèn waves, as in Uchida & Shibata's model. While the twisting of magnetic lines increases approaching the central parts of the disk, the ensuing strong gradient generated in the toroidal magnetic field opens up any vertically uniform magnetic structure. In particular for a hot corona = (v_s / v_A)² ~ 1, a jet can be launched from the inner portion of the disk surface, where the magnetic lines are dragged equatorially toward the central object and the inclination angle to the disk becomes 60°.

However, the wind does not reach a stationary state because the strong toroidal field in a well-defined region of the inner jet tends to recollimate the flow toward the axis, producing MHD shocks. In this way, a compact confined structure is launched from the disk along the poloidal field; the process can repeat periodically. Knots would then be produced automatically in magnetic topologies aligned to the rotation axis, without invoking irregularities in the accretion flow or other exotic scenarios. However, it must be remembered that in these simulations, the disk is assumed to be a fixed boundary and back-reaction effects are neglected.

Contopoulos (1995) has proposed another possible scenario for episodic outburst that we commented on above. He assumed that no poloidal field is present in the corona, only a toroidal component in the disk. The strong pressure gradient between the disk (B large) and the corona above it (B 0) forces plasma out perpendicularly to the disk. The explosively ejected plasma convects azimuthal magnetic field and is self-collimated. Contopoulos presented a simple time-dependent analysis of the process, showing that plasma is unstable to pinch instabilities that confine sheets of radial currents in the jets.