Annu. Rev. Astron. Astrophys. 1988. 36: 539-598 Copyright © 1998 by Annual Reviews. All rights reserved

4.3. Jet Instabilities

In their original proposal that extended radio galaxies are continuously powered by supersonic, relativistic outflows from galactic nuclei, Blandford & Rees (1974) pointed out that laboratory experiments (mostly subsonic) show that collimated beams maintain their directionality for relatively short distances (typically less than 10 times their diameter) owing to onset of fluid instabilities, shocks, boundary layer effects, and turbulent mixing with the external medium (Brown & Roshko 1974). Astrophysical supersonic and/or super-Alfvènic jets appear instead to be much longer lived, although they are modulated by knots, bends, and internal shocks of the same type observed in the laboratory. Therefore, several calculations have since been addressed to the question of pressure-confined jet stability (Blandford & Pringle 1976, Turland & Scheuer 1976, Ferrari et al 1978). In this section, we address jet stability against perturbations at the boundary layers with the confining medium created in the collimation zone, without considering perturbations coming from the flow's "head."

LINEAR KELVIN-HELMHOLTZ INSTABILITY    In the case of pressure-confined fluid beams in relative motion with respect to an external medium, the typical instability is the Kelvin-Helmholtz instability. If a ripple develops at the interface between the two fluids in relative motion, the flow over the ripple has to be faster and, therefore, according to the Bernoulli equation, exerts less pressure and allows the ripple to grow further. This causes mixing of the two fluids and transfer of momentum across the boundary, with a progressive destruction of collimation and slowing down of the flow (Chandrasekhar 1961, Gerwin 1968).

In our astrophysical context, this instability has been studied for supersonic, compressible, relativistic pressure-confined jets in cylindrical, slab, or conical geometries, both for axisymmetric and nonaxisymmetric perturbations, with and without a magnetic field, and with rotation; for a review, see Birkinshaw (1991). The linear stability analysis is based on perturbing the equilibrium shear layer between the two fluids with small-amplitude Fourier modes exp[-i ( t - k ^. r)] and linearizing the perturbed equations with matched boundary conditions across the shear. The resulting (algebraic) dispersion relation D(, k) = 0 is then studied to find modes with Im > 0 (locally growing modes) or Im k < 0 (spatially growing modes). When such modes exist, the equilibrium of the fluid can be destroyed, unless saturation effects stop the growth of the perturbations in the nonlinear regime. A systematic method to explore the complete stability diagram is presented by Bodo et al (1989).

Two types of modes exist in jets: ordinary surface modes, with amplitude steeply decreasing away from the interface, and reflected body modes, which affect the whole plasma in the jet. Body modes are typical of supersonic jets. While ordinary modes are already unstable in single-shear problems, reflected modes are stable in single shears but become resonantly unstable by reflections in a two-shear configuration, such as slabs or cylinders (Miles 1957). Their velocity with respect to the fluids is typically ~ ± v_rel / 2, half of their relative velocity. Resonant reflected modes have propagation wave vectors inclined by an angle ~ 1 / M_j over the shear surface. The most unstable wavelengths are typically

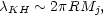(17)

with temporal growth times

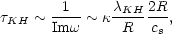(18)

where R is the beam transverse scale and 0.5 a factor depending on the specific geometry, mode, and density contrast; for magnetized beams, c_s is replaced by c_A. Ordinary modes dominate for M_j 22, and reflected modes above this limit. High density in the jet and strong magnetic fields reduce the effect of instability. In particular, the presence of magnetic fields, both longitudinal and transverse, has a stabilizing effect but mainly on small-wavelength modes. Thus, the development of turbulence and dissipation is avoided, and strongly magnetized jets can be considered substantially laminar. However, long-wavelength modes take over, though less rapidly, and may develop into strong modulation of the flow. Modes are completely stabilized for c_A / c_s 2.

A critical element in the instability evolution is the physical extent of the contact layer between the jet and the ambient medium. At the origin of jets, the so-called vortex sheet approximation, with steep velocity and density gradients across the layer, can be adopted, but after some distance, it may be more appropriate to use an extended transition zone that is created by matter entrainment and other nonlinear effects. Then all modes with wavelength shorter than the gradient scale are stabilized.

Instability time scales are rather short with respect to the propagation time scale, and therefore these modes can affect AGN jets soon after the exit from the nozzle. Long-wavelength modes modulate the morphology of the beam, while short wavelengths can give rise to a turbulent cascade that eventually leads to thermal dissipation and suprathermal particle acceleration.

In current-carrying jets, current-driven instabilities also must be considered. However, Appl & Camenzind (1992) have shown that their growth rates are always below that of Kelvin-Helmholtz modes.

Finally, we mention that rotation around the jet axis tends to stabilize ordinary modes at all wavelengths for low M_js and at small wavelengths for large M_js. This makes the importance of reflected modes in rotating jets (Bodo et al 1996).

FILAMENTATION INSTABILITY    Another type of intervening instability is the synchrotron "thermal" instability (Eilek & Caroff 1979, Bodo et al 1990). If the pressure in jets is mainly due to the relativistic electron component, synchrotron losses in regions compressed by fluid instability start the runaway effect of thermal instabilities (Field 1965). The compressed gas will radiate more and reduce the gas pressure, leading to further compression. In a situation out of equipartition, = P_rel / P_B 4, condensation modes with k_|| << k modulate the magnetic field into longitudinal filaments. These may be overpressured with respect to the external plasma and should appear brighter than the surrounding medium because of enhanced emission, provided a suitable input of fresh relativistic particles is guaranteed (Rossi et al 1993). These instabilities may be associated with the observations of radio and optical filaments in jets as M87 and 3C66B.

RESISTIVE INSTABILITIES    Most important instabilities in magnetically confined jets are reconnection modes. They develop in magnetic neutral sheets or shears across which a component of the field is inverted. A thin dissipation layer is produced at this sheet in which flux freezing is violated and magnetic flux can be annihilated (Biskamp 1994). For a beam with a helicoidal field wrapped around cylindrical surfaces, the equilibrium conditions predict a field pitch angle that decreases away from the axis. When a nonaxisymmetric perturbation is excited along the beam, its pitch angle will match the equilibrium pitch angle at some well-defined radius R_crit B / B_||. That cylindrical surface becomes a neutral sheet for the component of the field vector perpendicular to the perturbation wave vector. The end result is field annihilation and local heating and/or particle acceleration. The growth rate of these modes is relatively slow, but indications of an explosive nonlinear phase have been obtained in laboratory experiments (Ferrari 1984).

In the same context, Blackman has discussed how slow-mode shocks are formed in reconnection regions around magnetic X-point topologies (Blackman 1996). These shocks correspond to lower magnetic flux downstream than upstream of the front. Consistently fast particle acceleration can take place in regions of low = P_gas / P_B.